CHAPTER 1. LINES AND PLANES IN SPACE §1. Angles and
... 1.15. If the line is not perpendicular to plane Π and forms equal angles with two intersecting lines in this plane, then (by Problem 1.12) its projection to plane Π is parallel to the bisector of one of the two angles formed by these lines. We may assume that all the three lines meet at one point. I ...
... 1.15. If the line is not perpendicular to plane Π and forms equal angles with two intersecting lines in this plane, then (by Problem 1.12) its projection to plane Π is parallel to the bisector of one of the two angles formed by these lines. We may assume that all the three lines meet at one point. I ...
arXiv:1007.3607v1 [cs.CG] 21 Jul 2010 On k
... The notion of convexity is central in geometry. As such, it has been generalized in many ways and for different reasons. In this paper we consider a simple and intuitive generalization of convexity, which to the best of our knowledge has not been worked on. It leads to an appealing class of polygons ...
... The notion of convexity is central in geometry. As such, it has been generalized in many ways and for different reasons. In this paper we consider a simple and intuitive generalization of convexity, which to the best of our knowledge has not been worked on. It leads to an appealing class of polygons ...
The volume of the tetrahedron is
... • to be able to play their skills of observation, their spatial intuition, some fundamental geometric skills of geometry of the space; • for exploring geometric properties embedded in a geometric pattern origami • to experiece simple spatial geometric questions and even discover unexpected ...
... • to be able to play their skills of observation, their spatial intuition, some fundamental geometric skills of geometry of the space; • for exploring geometric properties embedded in a geometric pattern origami • to experiece simple spatial geometric questions and even discover unexpected ...
Locally convex topological vector spaces
... Note that the converse of Proposition 4.1.9 does not hold in any t.v.s.. Indeed, not every neighborhood of the origin contains another one which is a barrel. This means that not every t.v.s. has a basis of neighbourhood consisting of barrels. However, this is true for any locally convex t.v.s. Defin ...
... Note that the converse of Proposition 4.1.9 does not hold in any t.v.s.. Indeed, not every neighborhood of the origin contains another one which is a barrel. This means that not every t.v.s. has a basis of neighbourhood consisting of barrels. However, this is true for any locally convex t.v.s. Defin ...
7.1 Polygons and Exploring Interior Angles of Polygons Warm Up
... Objective: Identify, name, and describe polygons. A polygon is a plane figure that is formed by two or more segments such that each side intersects exactly two other sides, one at each endpoint. Each segment of a polygon is called a side. Any point where two sides meet is called a vertex. (The plura ...
... Objective: Identify, name, and describe polygons. A polygon is a plane figure that is formed by two or more segments such that each side intersects exactly two other sides, one at each endpoint. Each segment of a polygon is called a side. Any point where two sides meet is called a vertex. (The plura ...
Honors Geometry Lesson 1
... A __________________ is a closed plane figure with the following properties: – It is formed by three or more line segments called _____________________. – Each side intersects exactly two sides, one at each endpoint so that no two sides with a common endpoint are collinear. ...
... A __________________ is a closed plane figure with the following properties: – It is formed by three or more line segments called _____________________. – Each side intersects exactly two sides, one at each endpoint so that no two sides with a common endpoint are collinear. ...
Unit 6: Patterns in Shape
... An important feature of a quadrilateral or 4-bar linkage is that if any side is held fixed so it does not move and another side is moved, then the movement of the remaining sides is completely determined. The side that is fixed is called the frame. The two sides attached to the frame are called cran ...
... An important feature of a quadrilateral or 4-bar linkage is that if any side is held fixed so it does not move and another side is moved, then the movement of the remaining sides is completely determined. The side that is fixed is called the frame. The two sides attached to the frame are called cran ...
THE MEASURE OF ONE ANGLE IS 38 LESS THAN THE MEASURE
... SEGMENTS CALLED SIDES. 2) EACH SIDE INTERSECTS EXACTLY TWO SIDE, ONE AT EACH ENDPOINT, SO THAT NO TWO SIDES WITH A COMMON ENDPOINT ARE COLLINEAR EACH ENDPOINT OF A SIDE IS A VERTEX OF THE POLYGON. ...
... SEGMENTS CALLED SIDES. 2) EACH SIDE INTERSECTS EXACTLY TWO SIDE, ONE AT EACH ENDPOINT, SO THAT NO TWO SIDES WITH A COMMON ENDPOINT ARE COLLINEAR EACH ENDPOINT OF A SIDE IS A VERTEX OF THE POLYGON. ...
Non-expansive mappings in convex linear topological spaces
... so t h a t Q0(f(x)) < Q0(X) for x € K0. Moreover, Q0 is lower-semi continuous non-negative convex on K0. That Q0 is, indeed, normal follows from the minimality of K0\ for if C c: Ar0 is closed convex and non-trivial such t h a t Q0(X) = k = constant on C, then actually C = {x e K0\Q(X) < k} and is a ...
... so t h a t Q0(f(x)) < Q0(X) for x € K0. Moreover, Q0 is lower-semi continuous non-negative convex on K0. That Q0 is, indeed, normal follows from the minimality of K0\ for if C c: Ar0 is closed convex and non-trivial such t h a t Q0(X) = k = constant on C, then actually C = {x e K0\Q(X) < k} and is a ...
Compact hyperbolic tetrahedra with non
... Proof: Let H be the space of closed half-spaces of H3 ; clearly H is a 3dimensional manifold. Let O∆ be the set of marked hyperbolic polyhedra realizing ∆. By forgetting this marking, an element of O∆ is a 4-tuple of halfspaces that intersect in a polyhedron realizing ∆. This induces a mapping from ...
... Proof: Let H be the space of closed half-spaces of H3 ; clearly H is a 3dimensional manifold. Let O∆ be the set of marked hyperbolic polyhedra realizing ∆. By forgetting this marking, an element of O∆ is a 4-tuple of halfspaces that intersect in a polyhedron realizing ∆. This induces a mapping from ...
7•2 Naming and Classifying Polygons and Polyhedrons
... A polygon is a closed figure that has three or more sides. Each side is a line segment, and the sides meet only at the endpoints, or vertices. This figure is a polygon. ...
... A polygon is a closed figure that has three or more sides. Each side is a line segment, and the sides meet only at the endpoints, or vertices. This figure is a polygon. ...
Section 1.6-Classify Polygons
... Is a closed plane figure with the following properties: 1. It is formed by three or more line segments called sides 2. Each side intersects exactly two sides, one at each endpoint, so that no two sides with a common endpoint are collinear. ...
... Is a closed plane figure with the following properties: 1. It is formed by three or more line segments called sides 2. Each side intersects exactly two sides, one at each endpoint, so that no two sides with a common endpoint are collinear. ...
Geometry EOC Assessment - Florida Department Of Education
... • apply transformations to polygons to determine congruence, similarity, or symmetry; • solve problems by using or deriving formulas for perimeter and area of polygons; • determine how changes in dimensions affect the perimeter or area of triangles or quadrilaterals; • use coordinate geometry to fin ...
... • apply transformations to polygons to determine congruence, similarity, or symmetry; • solve problems by using or deriving formulas for perimeter and area of polygons; • determine how changes in dimensions affect the perimeter or area of triangles or quadrilaterals; • use coordinate geometry to fin ...
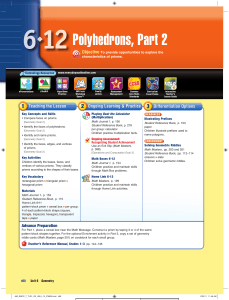
Polyhedrons, Part 2
... page, discuss children’s work as a class. Ask several children to name the shape of the bases of their prisms. Ask: What is the shape of the faces that are not bases? rectangles Prisms are named after the shapes of their bases. For example, the bases of a rectangular prism are rectangles. A prism wh ...
... page, discuss children’s work as a class. Ask several children to name the shape of the bases of their prisms. Ask: What is the shape of the faces that are not bases? rectangles Prisms are named after the shapes of their bases. For example, the bases of a rectangular prism are rectangles. A prism wh ...
5 Properties of shapes and solids
... If you extend the length of one side of a triangle you form another angle outside the triangle. Angles formed outside the triangle in this way are called exterior angles. If you tear off the angles of any triangle and place them against a straight edge (180°) you can see that the interior angles add ...
... If you extend the length of one side of a triangle you form another angle outside the triangle. Angles formed outside the triangle in this way are called exterior angles. If you tear off the angles of any triangle and place them against a straight edge (180°) you can see that the interior angles add ...
Warm Up: Investigating the Properties of Quadrilaterals
... • You may choose to work as a group or by yourself. ...
... • You may choose to work as a group or by yourself. ...
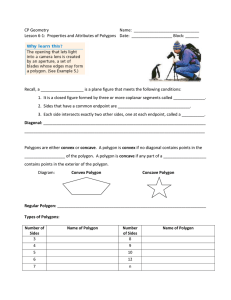
CP Geometry Name: Lesson 6-1: Properties and Attributes of
... Recall, a ___________________ is a plane figure that meets the following conditions: 1. It is a closed figure formed by three or more coplanar segments called ______________. 2. Sides that have a common endpoint are ________________________________. 3. Each side intersects exactly two other sides, o ...
... Recall, a ___________________ is a plane figure that meets the following conditions: 1. It is a closed figure formed by three or more coplanar segments called ______________. 2. Sides that have a common endpoint are ________________________________. 3. Each side intersects exactly two other sides, o ...
Camp 1 Lantern Packet
... Now using what you learned about the interior angle total (sum) of a triangle, prove the total angles of these other polygons by dividing the shapes into the fewest number of triangles as possible. Use those triangles to calculate the sums of the new shapes. ...
... Now using what you learned about the interior angle total (sum) of a triangle, prove the total angles of these other polygons by dividing the shapes into the fewest number of triangles as possible. Use those triangles to calculate the sums of the new shapes. ...
Convexity and convex hulls
... total complexity of all the facets. But this is no good even in two dimensions. The Upper Bound Theorem due to McMullen[3] states that the total complexity of the convex hull of n points in d dimensions is O(nbd/2c ). The proof is quite complicated and involves the idea of a shelling of a polytope. ...
... total complexity of all the facets. But this is no good even in two dimensions. The Upper Bound Theorem due to McMullen[3] states that the total complexity of the convex hull of n points in d dimensions is O(nbd/2c ). The proof is quite complicated and involves the idea of a shelling of a polytope. ...
Polygons Notes
... A polygon is a plane figure that meets the following conditions: a) A shape that is formed by three or more segments called_______________. b) Each side intersects exactly two other sides, one at each endpoint, called the ________________. ...
... A polygon is a plane figure that meets the following conditions: a) A shape that is formed by three or more segments called_______________. b) Each side intersects exactly two other sides, one at each endpoint, called the ________________. ...
Geometry: From Triangles to Quadrilaterals and Polygons .
... More definitions for polygons Convex polygon: Defines a shape that curves outward; opposite of concave. A geometric figure is convex if every line segment connecting interior points is entirely contained within the figure's interior Concave polygon: Defines a shape that curves inward; opposite of c ...
... More definitions for polygons Convex polygon: Defines a shape that curves outward; opposite of concave. A geometric figure is convex if every line segment connecting interior points is entirely contained within the figure's interior Concave polygon: Defines a shape that curves inward; opposite of c ...
UNIT VII
... Recall that a regular polygon is __a polygon that has bot equal sides and equal angles______________. ...
... Recall that a regular polygon is __a polygon that has bot equal sides and equal angles______________. ...
Sample
... 79. A can of beans is in the shape of a right circular cylinder. To recycle the can, the top and bottom are cut out and the remaining part of the can is cut and laid flat. Describe the shapes of the pieces of metal that remain for recycling. 80. Water is flowing along a stream at the rate of 1200 ga ...
... 79. A can of beans is in the shape of a right circular cylinder. To recycle the can, the top and bottom are cut out and the remaining part of the can is cut and laid flat. Describe the shapes of the pieces of metal that remain for recycling. 80. Water is flowing along a stream at the rate of 1200 ga ...
Notes on Rigidity Theory James Cruickshank
... A face of a polyhedral graph is a non-separating cycle without repeated vertices in the graph. A polyhedron is a polyhedral graph together with an embedding of the vertex set into some three dimensional real vector space such that each face of the polyhedral graph is embedded into a plane. It is imp ...
... A face of a polyhedral graph is a non-separating cycle without repeated vertices in the graph. A polyhedron is a polyhedral graph together with an embedding of the vertex set into some three dimensional real vector space such that each face of the polyhedral graph is embedded into a plane. It is imp ...
Polyhedron

In elementary geometry, a polyhedron (plural polyhedra or polyhedrons) is a solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. The word polyhedron comes from the Classical Greek πολύεδρον, as poly- (stem of πολύς, ""many"") + -hedron (form of ἕδρα, ""base"" or ""seat"").Cubes and pyramids are examples of polyhedra.A polyhedron is said to be convex if its surface (comprising its faces, edges and vertices) does not intersect itself and the line segment joining any two points of the polyhedron is contained in the interior or surface.A polyhedron is a 3-dimensional example of the more general polytope in any number of dimensions.
![arXiv:1007.3607v1 [cs.CG] 21 Jul 2010 On k](http://s1.studyres.com/store/data/014301021_1-0b834295d3acb0403d454bb0d0019afe-300x300.png)