1-6 Guided Notes STUDENT EDITION
... Then evaluate one of the expressions to find a side length when x = _4_ 4x + 3 = 4(_4_) + 3 = _19_ The length of a side is _19_ millimeters. Complete the following exercises. 3. Classify the polygon by the number of sides. Tell whether the polygon is equilateral, equiangular, or regular. ...
... Then evaluate one of the expressions to find a side length when x = _4_ 4x + 3 = 4(_4_) + 3 = _19_ The length of a side is _19_ millimeters. Complete the following exercises. 3. Classify the polygon by the number of sides. Tell whether the polygon is equilateral, equiangular, or regular. ...
Polygons_worksheet3 - Penns Valley Math Resources
... If a polygon has all interior angles congruent, we say it is equiangular. If a polygon has all edges and all vertices congruent, we say it is regular. Drawings of some regular polygons are shown on the right. Notice that the measure of one vertex is given in each of the pictures. Since the polygons ...
... If a polygon has all interior angles congruent, we say it is equiangular. If a polygon has all edges and all vertices congruent, we say it is regular. Drawings of some regular polygons are shown on the right. Notice that the measure of one vertex is given in each of the pictures. Since the polygons ...
arXiv:math/0607084v3 [math.NT] 26 Sep 2008
... Suppose that A inverts the order of the vertices, that is, A(vi ) = vt+n−1−i for all i = 0, 1, . . . , n−1. Then, either the operator A′ such that A′ (Vet ) = Ve2t , or the operator A′ A (for which, obviously, A′ A(Ve0 ) = Ve2t ) preserves the order of the vertices. Therefore we may assume that A p ...
... Suppose that A inverts the order of the vertices, that is, A(vi ) = vt+n−1−i for all i = 0, 1, . . . , n−1. Then, either the operator A′ such that A′ (Vet ) = Ve2t , or the operator A′ A (for which, obviously, A′ A(Ve0 ) = Ve2t ) preserves the order of the vertices. Therefore we may assume that A p ...
Lesson - Schoolwires
... properties of two-dimensional figures and three dimensional solids (polyhedra), including the number of edges, faces, vertices, and types of faces. ...
... properties of two-dimensional figures and three dimensional solids (polyhedra), including the number of edges, faces, vertices, and types of faces. ...
tetrahedron - PlanetMath.org
... remainder of this entry, we shall assume that all tetrahedra are non-degenerate. If all six edges of a tetrahedron are equal, it is called a regular tetrahedron. The faces of a regular tetrahedron are equilateral triangles. ...
... remainder of this entry, we shall assume that all tetrahedra are non-degenerate. If all six edges of a tetrahedron are equal, it is called a regular tetrahedron. The faces of a regular tetrahedron are equilateral triangles. ...
Polygons - mathmastermindgeometry
... A polygon can specifically be labeled by placing a capital letter on each vertex, moving consecutively around the figure in either a clockwise or counterclockwise direction. This helps to distinguish between two similar polygons. If two pentagons were placed next to each other telling the difference ...
... A polygon can specifically be labeled by placing a capital letter on each vertex, moving consecutively around the figure in either a clockwise or counterclockwise direction. This helps to distinguish between two similar polygons. If two pentagons were placed next to each other telling the difference ...
rhombic - The Math Forum @ Drexel
... Arrange students in groups of 3 or 4. Each group needs a cup or Ziploc bag containing 12 blue struts, 8 yellow struts, and 9 white balls, and each student in the group needs a worksheet. If you have enough Zome tools, each group should also get several sets of 4 blue, 4 yellow, and 5 balls to make ...
... Arrange students in groups of 3 or 4. Each group needs a cup or Ziploc bag containing 12 blue struts, 8 yellow struts, and 9 white balls, and each student in the group needs a worksheet. If you have enough Zome tools, each group should also get several sets of 4 blue, 4 yellow, and 5 balls to make ...
MA.912.G.2 Geometry: Standard 2: Polygons
... Participatory: Match two or more objects with four-sided shapes (quadrilaterals), based on a given feature, such as length of side or size of the area. ...
... Participatory: Match two or more objects with four-sided shapes (quadrilaterals), based on a given feature, such as length of side or size of the area. ...
Geometry - macgeometrystudent
... What observations can you make? Using these examples, can you form a good definition of each? Concave: ...
... What observations can you make? Using these examples, can you form a good definition of each? Concave: ...
Section 9.1- Basic Notions
... • A simple closed surface has exactly one interior, has no holes, and is hollow. It separates space into interior, surface, and exterior. • A sphere is the set of all points at a given distance from a given point, the center. • A solid is the set of all points on a simple closed surface along with a ...
... • A simple closed surface has exactly one interior, has no holes, and is hollow. It separates space into interior, surface, and exterior. • A sphere is the set of all points at a given distance from a given point, the center. • A solid is the set of all points on a simple closed surface along with a ...
Two-Dimensional Figures
... are all segments. A polygon’s sides intersect exactly two other sides, but only at their endpoints. Examples: ...
... are all segments. A polygon’s sides intersect exactly two other sides, but only at their endpoints. Examples: ...
Analytical Calculation of Geodesic Lengths and Angle Measures on
... In art such as modular origami and architecture, regular and semi-regular polyhedra have been popular subjects [2][3]. These polyhedra have regular polygons as their faces and edges with the same length. Five Platonic solids and thirteen Archimedean solids in Figure 1 are convex regular and semi-reg ...
... In art such as modular origami and architecture, regular and semi-regular polyhedra have been popular subjects [2][3]. These polyhedra have regular polygons as their faces and edges with the same length. Five Platonic solids and thirteen Archimedean solids in Figure 1 are convex regular and semi-reg ...
Random Realization of Polyhedral Graphs as Deltahedra
... Figure 8 shows graphs which contain the same partial structures and their realized polyhedra. As shown in Figure 8, when we form a larger deltahedron by connecting two smaller deltahedra along a single face, the original shapes do not change and the graph of the appended deltahedron can be embedded ...
... Figure 8 shows graphs which contain the same partial structures and their realized polyhedra. As shown in Figure 8, when we form a larger deltahedron by connecting two smaller deltahedra along a single face, the original shapes do not change and the graph of the appended deltahedron can be embedded ...
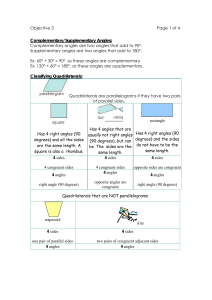
Objective 3 Page 1 of 4 Complementary/Supplementary Angles
... The scale factor from one figure to the other is the number you multiply one figure by to get to the other. Enlargement : The figure is bigger than the original. The scale factor is greater than 1. The picture to the left is an ...
... The scale factor from one figure to the other is the number you multiply one figure by to get to the other. Enlargement : The figure is bigger than the original. The scale factor is greater than 1. The picture to the left is an ...
Solutions - Austin Mohr
... A regular triangle has (3−2)⋅180 = 180 degrees total, which means each angle measures 180 3 = 60 degrees. A regular pentagon has (5 − 2) ⋅ 180 = 540 degrees total, which means each angle measures 540 5 = 108 degrees. There are two things to keep in mind when forming polyhedra of any kind: 1. There m ...
... A regular triangle has (3−2)⋅180 = 180 degrees total, which means each angle measures 180 3 = 60 degrees. A regular pentagon has (5 − 2) ⋅ 180 = 540 degrees total, which means each angle measures 540 5 = 108 degrees. There are two things to keep in mind when forming polyhedra of any kind: 1. There m ...
Geometry Test A 6 – 1 to 6 – 3
... In 1 – 3 decide whether the figure is a polygon. If it isn’t explain why not. If it is, state whether it is convex. ...
... In 1 – 3 decide whether the figure is a polygon. If it isn’t explain why not. If it is, state whether it is convex. ...
Triangles and Squares
... Line-circle crossings equal point-circle horizon Preserves point-line incidences! (a form of projective duality) ...
... Line-circle crossings equal point-circle horizon Preserves point-line incidences! (a form of projective duality) ...
Day-34 Addendum: Polyhedral Surfaces Intro - Rose
... that consists of a set of vertices (points) and edges where the edges are straight lines that join to points. More generally, a polygon is a special type of planar graph (from Discrete and Combinatorial Mathematics). For a polygon, the edges can be described as an ordered list of the edges, where ed ...
... that consists of a set of vertices (points) and edges where the edges are straight lines that join to points. More generally, a polygon is a special type of planar graph (from Discrete and Combinatorial Mathematics). For a polygon, the edges can be described as an ordered list of the edges, where ed ...
Ch 1-2
... Postulate 2.1 – Every line contains at least two distinct points. Postulate 2.2 – Two points are contained in one and only one line. Postulate 2.3 – If two points are in a plane the line containing these points is also in the plane. Postulate 2.4 – Three non-collinear points are contained in one and ...
... Postulate 2.1 – Every line contains at least two distinct points. Postulate 2.2 – Two points are contained in one and only one line. Postulate 2.3 – If two points are in a plane the line containing these points is also in the plane. Postulate 2.4 – Three non-collinear points are contained in one and ...
Section 2.1 – Undefined terms, postulates, segments and angles
... Postulate 2.1 – Every line contains at least two distinct points. Postulate 2.2 – Two points are contained in one and only one line. Postulate 2.3 – If two points are in a plane the line containing these points is also in the plane. Postulate 2.4 – Three non-collinear points are contained in one and ...
... Postulate 2.1 – Every line contains at least two distinct points. Postulate 2.2 – Two points are contained in one and only one line. Postulate 2.3 – If two points are in a plane the line containing these points is also in the plane. Postulate 2.4 – Three non-collinear points are contained in one and ...
Sec 6. 1 Prac C
... 9. An equilateral hexagon that is not equiangular 10. An equiangular hexagon that is not equilateral 11. An equiangular quadrilateral that is not regular ...
... 9. An equilateral hexagon that is not equiangular 10. An equiangular hexagon that is not equilateral 11. An equiangular quadrilateral that is not regular ...
Eng
... Area: The number of square units it takes to completely fill a space or surface. Bases of a Prism: The two faces formed by congruent polygons that lie in parallel planes, all of the other faces being parallelograms. Cubic Units: Volume of the solids is measured in Cubic Units. Edge: The intersection ...
... Area: The number of square units it takes to completely fill a space or surface. Bases of a Prism: The two faces formed by congruent polygons that lie in parallel planes, all of the other faces being parallelograms. Cubic Units: Volume of the solids is measured in Cubic Units. Edge: The intersection ...
histm008b
... fill space in a regular manner are the cube and the regular tetrahedron, but he did not give reasons for his assertion. Between the time of Aristotle and the late 15th century, there were many attempts to understand and prove his assertion about filling space with solid regular tetrahedra, but in th ...
... fill space in a regular manner are the cube and the regular tetrahedron, but he did not give reasons for his assertion. Between the time of Aristotle and the late 15th century, there were many attempts to understand and prove his assertion about filling space with solid regular tetrahedra, but in th ...
Polyhedron

In elementary geometry, a polyhedron (plural polyhedra or polyhedrons) is a solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. The word polyhedron comes from the Classical Greek πολύεδρον, as poly- (stem of πολύς, ""many"") + -hedron (form of ἕδρα, ""base"" or ""seat"").Cubes and pyramids are examples of polyhedra.A polyhedron is said to be convex if its surface (comprising its faces, edges and vertices) does not intersect itself and the line segment joining any two points of the polyhedron is contained in the interior or surface.A polyhedron is a 3-dimensional example of the more general polytope in any number of dimensions.

![arXiv:math/0607084v3 [math.NT] 26 Sep 2008](http://s1.studyres.com/store/data/014838781_1-63e86760b3063903e159a8155f16fef1-300x300.png)