Polygon Angle-Sum Theorem - Mustang-Math
... Classifying Polygons Polygon: Closed plane figure with at least three sides that are segments intersecting only at their endpoints, and no adjacent sides are collinear. ...
... Classifying Polygons Polygon: Closed plane figure with at least three sides that are segments intersecting only at their endpoints, and no adjacent sides are collinear. ...
Lesson 3.5 The Polygon Angle
... Classify each polygon by its sides. Identify each as convex or concave. ...
... Classify each polygon by its sides. Identify each as convex or concave. ...
Chapter 6 Polygons and Quadrilaterals
... The car at each vertex of a Ferris wheel holds a maximum of 5 people. The sum of the measures of the angles of the Ferris wheel is 7740. What is the maximum number of people that the Ferris wheel ...
... The car at each vertex of a Ferris wheel holds a maximum of 5 people. The sum of the measures of the angles of the Ferris wheel is 7740. What is the maximum number of people that the Ferris wheel ...
The Euler characteristic of an even
... the Euler characteristic of this surface is related to the Euler characteristic of the entire space. If we integrate over a probability space of functions f , the expectation of the curvatures K(x, f ) of these surfaces at a vertex x is related to the Euler curvature K(x). Because scalar curvature c ...
... the Euler characteristic of this surface is related to the Euler characteristic of the entire space. If we integrate over a probability space of functions f , the expectation of the curvatures K(x, f ) of these surfaces at a vertex x is related to the Euler curvature K(x). Because scalar curvature c ...
Why i? The Historical Roots of “Imaginary” Numbers The first
... to be wished therefore that negative roots had never been admitted into algebra or were again discarded from it: for if this were done, there is good reason to imagine, the objections which many learned and ingenious men now make to algebraic computations, as being obscure and perplexed with almost ...
... to be wished therefore that negative roots had never been admitted into algebra or were again discarded from it: for if this were done, there is good reason to imagine, the objections which many learned and ingenious men now make to algebraic computations, as being obscure and perplexed with almost ...
12.1 Exploring Solids
... a. This is a polyhedron. It has 5 faces, 6 vertices, and 9 edges. b. This is not a polyhedron. Some of its faces are not polygons. c. This is a polyhedron. It has 7 faces, 7 vertices, and 12 edges. ...
... a. This is a polyhedron. It has 5 faces, 6 vertices, and 9 edges. b. This is not a polyhedron. Some of its faces are not polygons. c. This is a polyhedron. It has 7 faces, 7 vertices, and 12 edges. ...
The Euler Line and the Nine-Point
... and several other defined points. Above on the circle lie E, F, and G, which are the midpoints of the sides BC , AC , and AB respectively. There are points T, H, and I that are the feet of the altitudes of the triangle. The segments that connect the orthocenter with the vertices, AO , CO , and BO , ...
... and several other defined points. Above on the circle lie E, F, and G, which are the midpoints of the sides BC , AC , and AB respectively. There are points T, H, and I that are the feet of the altitudes of the triangle. The segments that connect the orthocenter with the vertices, AO , CO , and BO , ...
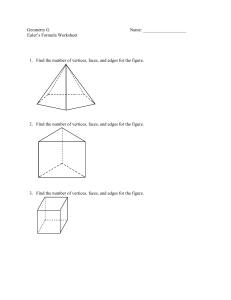
Euler`s Formula Worksheet 1. Find the
... 6. A polyhedron has 6 faces and 7 vertices. How many edges does it have? Explain your answer. 7. A polyhedron has 9 faces and 21 edges. How many vertices does it have? Explain your answer. 8. Use Euler’s Theorem to calculate how many vertices a polyhedron has if it has 12 faces and 30 edges. 9. Use ...
... 6. A polyhedron has 6 faces and 7 vertices. How many edges does it have? Explain your answer. 7. A polyhedron has 9 faces and 21 edges. How many vertices does it have? Explain your answer. 8. Use Euler’s Theorem to calculate how many vertices a polyhedron has if it has 12 faces and 30 edges. 9. Use ...
On the works of Euler and his followers on spherical geometry
... them became eventually his colleagues at the Academy of Sciences of Saint Petersburg. These works of Euler and his followers contain a wealth of ideas that have not got the attention they deserve from the working geometers. The results that we survey can be classified into three categories. The firs ...
... them became eventually his colleagues at the Academy of Sciences of Saint Petersburg. These works of Euler and his followers contain a wealth of ideas that have not got the attention they deserve from the working geometers. The results that we survey can be classified into three categories. The firs ...
Anders Johan Lexell

Anders Johan Lexell (24 December 1740 – 11 December [O.S. 30 November] 1784) was a Finnish-Swedish astronomer, mathematician, and physicist who spent most of his life in Russia, where he is known as Andrei Ivanovich Leksel (Андрей Иванович Лексель).Lexell made important discoveries in polygonometry and celestial mechanics; the latter led to a comet named in his honour. La Grande Encyclopédie states that he was the prominent mathematician of his time who contributed to spherical trigonometry with new and interesting solutions, which he took as a basis for his research of comet and planet motion. His name was given to a theorem of spherical triangles.Lexell was one of the most prolific members of the Russian Academy of Sciences at that time, having published 66 papers in 16 years of his work there. A statement attributed to Leonhard Euler expresses high approval of Lexell's works: ""Besides Lexell, such a paper could only be written by D'Alambert or me"". Daniel Bernoulli also praised his work, writing in a letter to Johann Euler ""I like Lexell's works, they are profound and interesting, and the value of them is increased even more because of his modesty, which adorns great men"".Lexell was unmarried, and kept up a close friendship with Leonhard Euler and his family. He witnessed Euler's death at his house and succeeded Euler to the chair of the mathematics department at the Russian Academy of Sciences, but died the following year. The asteroid 2004 Lexell is named in his honour, as is the lunar crater Lexell.