Download Oscillations - Pearland ISD

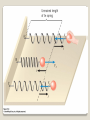
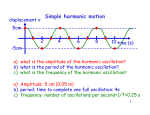
Oscillations
Dawson High School
AP Physics 1
© Mark Lesmeister/Pearland ISD

Selected graphics from Cutnell and Johnson, Physics
9e: Instructor’s Companion Site, © 2015 John Wiley
and Sons.

Selected graphic from Serway and Faughn, Holt
Physics, © 2002 Holt, Rinehart and Winston
Acknowledgements
Introduction

Questions to observe:
◦ Does the rate of oscillation
depend on the amplitude of the
motion?
◦ Does the rate of oscillation
depend on the mass being
oscillated?
Observing Oscillating Systems
Many types of systems undergo oscillation.
Horizontal Spring and Mass
Oscillations
Oscillation is also called periodic motion.
Oscillations
Oscillations can occur when there is a restoring
force.
Restoring Force
The frequency f is the number of oscillations
per unit time.
The period T is the time for one oscillation.
1
f 
T
Horizontal Spring and Mass
Describing Oscillations

The maximum
displacement
from equilibrium
is called the
amplitude.
Amplitude
FELASTIC = -k x
FELASTIC
x
Review: Hooke’s Law
Lab: Period of a Spring and
Mass System
Determine quantitatively
the effect on the period
when:


the mass is increased.
the amplitude is varied.
HorizontalSpring and Mass
Source: Wikipedia

Simple Harmonic Motion of a
Spring and Mass System

When the restoring force is proportional
to the displacement, the result is simple
harmonic motion.
F  kx
Simple Harmonic Motion
Simple Harmonic Motion Plot
Simple harmonic motion forms a sinusoidal
graph.
Simple Harmonic Motion
Simple Harmonic Motion Plot
Simple Harmonic Motion

The restoring
force, and thus
the acceleration,
are at a maximum
when
displacement is
maximum.
Maxima and minima for SHM

The velocity is at a
maximum when
the displacement
is zero.
Maxima and Minima for SHM

Displacement:

Velocity:

Acceleration
Graphs for SHM

The frequency and period depend on the
setup, and are independent of the
amplitude.
Simple Harmonic Motion

The frequency and period for a spring and
mass are
1
f 
2
k
m
m
T  2
k
Frequency and Period of a Spring
and Mass System

If there is no friction, mechanical energy
is conserved.
U SPRING  12 kx2
U MAX
ME  U SPRING MAX  12 kA2
K  ME  U  12 kA2  12 kx2
-A
0
Energy of a Spring and Mass
System
A
ME
U  kx
1
2
2
x

In an ideal system, the mass-spring
system would oscillate indefinitely.

Damping occurs when friction
retards the motion.
◦ Damping causes the system to come to
rest after a period of time.
◦ If we observe the system over a short
period of time, damping is minimal, and
we can treat the system like as ideal.
Damping
10.1.4. An ideal spring is hung vertically from a device that displays the force
exerted on it. A heavy object is then hung from the spring and the display on
the device reads W, the weight of the spring plus the weight of the object, as
both sit at rest. The object is then pulled downward a small distance and
released. The object then moves in simple harmonic motion. What is the
behavior of the display on the device as the object moves?
a) The force remains constant while the object oscillates.
b) The force varies between W and +W while the object oscillates.
c) The force varies between a value near zero newtons and W while the object
oscillates.
d) The force varies between a value near zero newtons and 2W while the object
oscillates.
e) The force varies between W and 2W while the object oscillates.
10.3.1. An ideal spring is hung vertically from a fixed support. When an object of mass
m is attached to the end of the spring, it stretches by a distance y. The object is then
lifted and held to a height y +A, where A << y. Which one of the following
statements concerning the total potential energy of the object is true?
a) The total potential energy will be equal to zero joules.
b) The total potential energy will decrease and be equal to the gravitational potential
energy of the object.
c) The total potential energy will decrease and be equal to the elastic potential energy of
the spring.
d) The total potential energy will decrease and be equal to the sum of elastic potential
energy of the spring and the gravitational potential energy of the object.
e) The total potential energy will increase and be equal to the sum of elastic potential
energy of the spring and the gravitational potential energy of the object.
10.3.2. A block is attached to the end of a horizontal ideal spring and rests on a
frictionless surface. The other end of the spring is attached to a wall. The block
is pulled away from the spring’s unstrained position by a distance x0 and given
an initial speed of v0 as it is released. Which one of the following statements
concerning the amplitude of the subsequent simple harmonic motion is true?
a) The amplitude will depend on whether the initial velocity of the block is in the +x
or the x direction.
b) The amplitude will be less than x0.
c) The amplitude will be equal to x0.
d) The amplitude will be greater than x0.
e) The amplitude will depend on whether the initial position of the block is in the +x
or the x direction relative to the unstrained position of the spring.
10.3.5. Block A has a mass m and block B has a mass 2m. Block A is pressed
against a spring to compress the spring by a distance x. It is then
released such that the block eventually separates from the spring and it
slides across a surface where the friction coefficient is µk. The same
process is applied to block B. Which one of the following statements
concerning the distance that each block slides before stopping is correct?
a) Block A slides one-fourth the distance that block B slides.
b) Block A slides one-half the distance that block B slides.
c) Block A slides the same distance that block B slides.
d) Block A slides twice the distance that block B slides.
e) Block A slides four times the distance that block B slides.
Pendulum Motion

The forces on the bob
are the weight mg
and the tension T.

The restoring force is
the tangential
component of the
weight, -mg sin θ .
Pendulum Motion

For small angles,
sin   

The restoring force
is
s
F  mg  mg
L

The motion is SHM
Pendulum Motion

The mass cancels
out when Newton’s
2nd Law is applied:
s
F  mg  ma
L
s
g a
L
Pendulum Motion

The frequency and
period are
1
f 
2
g
L
L
T  2
g
Pendulum Motion
From Holt Physics © Holt, Rinehart
10.4.1. You would like to use a simple pendulum to determine the local
value of the acceleration due to gravity, g. Consider the following
parameters: (1) pendulum length, (2) mass of the object at the free end
of the pendulum, (3) the period of the pendulum as it swings in simple
harmonic motion, (4) the amplitude of the motion. Which of these
parameters must be measured to find a value for g?
a) 1 only
b) 2 only
c) 3 and 4 only
d) 1 and 3 only
e) 1, 2, and 4 only
10.4.2. At the surface of Mars, the acceleration due to gravity is
3.71 m/s2. On Earth, a pendulum that has a period of one
second has a length of 0.248 m. What is the length of a
pendulum on Mars that oscillates with a period of one
second?
a) 0.0940 m
b) 0.143 m
c) 0.248 m
d) 0.296 m
e) 0.655 m