Download Chapter 21: Electric Charge and Electric Field

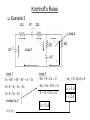
Chapter 25: Electric Circuits
Resistors in Series and Parallel
 Resistors
in series
V
V
IR1  IR2  V  IReq  Req  R1  R2
In general you can extend this formula to : Req  i Ri
Resistors in Series and Parallel
 Resistors
in parallel
V
V
V
V V
1
1
1
I  I1  I 2 
 

 
Req R1 R2
Req R1 R2
I1 R2
V  I1 R1  I 2 R2  
I 2 R1
1
1
In general you can extend this formula to :
 i
Req
Ri
Resistors in Series and Parallel
 Example
1:
Resistors in Series and Parallel
 Example:
(cont’d)
I2
R2
I4
R4
I3
I
R3
V
I  V / Req  12 V/2   6 A
I 3  V / R3  12 V/3   4 A
I 2  I 4  V /( R2  R3 )  12 V/(2  4 )  2 A
Resistors in Series and Parallel
 Example:
(cont’d)
Kirchhoff’s Rules
 Introduction
• Many practical resistor networks cannot be reduced to simple series-parallel
combinations (see an example below).
• Terminology:
-A junction in a circuit is a point where three or more conductors meet.
-A loop is any closed conducting path.
junction
Loop 2
i
i
i2
i1
i
Loop 1
i
i2
junction
Kirchhoff’s Rules
 Kirchhoff’s
junction rule
• The algebraic sum of the currents into any junction is zero:
 I  0 at any junction
Kirchhoff’s Rules
 Kirchhoff’s
loop rule
• The algebraic sum of the potential differences in any loop, including
those associated with emfs and those of resistive elements, must equal
zero.
V  0 for any loop
Kirchhoff’s Rules

Rules for Kirchhoff’s loop rule
 I  0 at any junction
V  0 for any loop
Kirchhoff’s Rules

Rules for Kirchhoff’s loop rule (cont’d)
Kirchhoff’s Rules

Solving problems using Kirchhoff’s rules
Kirchhoff’s Rules

Example 1
Kirchhoff’s Rules

Example 1 (cont’d)
Kirchhoff’s Rules

Example 1 (cont’d)
Kirchhoff’s Rules
Find
all the currents
 Example
2 including directions.
Loop 2
i
i
i2
i1
i
Loop 1
i
Loop 1
0  8V  4V  4V  3i  2i1
0  8  3i1  3i 2  2i1
0  8  5i1  3i 2
multiply by 2
i = i1+ i2
i2
Loop 2
 6i 2  4  2i1  0
 6i 2  16  10i1  0
0  12  12i1  0
i1  1A
 6i2  4  2(1A)  0
i 2  1A
i  2A
Electrical Measuring Instruments

Galvanometer
To be discussed in a later
class.
Electrical Measuring Instruments

Ammeter
Electrical Measuring Instruments

Ammeter (cont’d)
Electrical Measuring Instruments

Voltmeter
R-C Circuits

Charging a capacitor
R-C Circuits

Charging a capacitor (cont’d)
R-C Circuits

Charging a capacitor (cont’d)
R-C Circuits

Charging a capacitor (cont’d)
R-C Circuits

Charging a capacitor (cont’d)
R-C Circuits

Discharging a capacitor
R-C Circuits

Discharging a capacitor (cont’d)
R-C Circuits

Discharging a capacitor (cont’d)
Exercises

Problem 1
The resistance of a galvanometer coil is 25.0 ,
and the current required for full-scale deflection
is 500 mA.
a) Show in a diagram how to convert the galvanometer to an ammeter reading 20.0 mA full scale,
and compute the shunt resistance.
b) Show how to convert the galvanometer to a
voltmeter reading 500 mV full scale, and compute
the series resistance.
Solution
a) For a 20-mA ammeter, the two resistance are in
parallel:
Vc=Vs->IcRc=IsRs->(500 x 10-6 A)(25.0 ) =
(20 x 10-3 A – 500 x 10-6 A)Rs-> Rs=0.641 .
b) For a 500-mV voltmeter, the resistances are in
series:
Vab=I(Rc+Rs)->Rs=Vab/I – Rc ->
Rs=500 x 10-3 V / 500 x 10-6 A – 25.0  = 975 .
Rc=25.0 
500 mA
20 mA
Rs
a) ammeter
Rc=25.0 
Rs
a
Vab=500 mV b
b) voltmeter
500 mA
Exercises
20.0 V
+
I1
loop 2 (right) :
36  5I 2  4( I 2  I1 )  0  36  4 I1  9 I 2  0
Solving these two equations for the currents :
I1  5.21 A, I 2  6.32 A. The current th at goes through
4  is I 2  I1  1.11 A.
I2
4.00 
20  14  2 I1  4( I 2  I1 )  0  6  6 I1  4 I 2  0
2.00 
loop 1 (left) :
5.00 
+
v
v
+
I1-I2
14.0 V
v
Problem 2
v

36.0 V
Exercises
6.00 
V=18.0 V
6.00 mF
b
a
S
3.00 
 Problem 3
a) What is the potential of point a with respect
to point b when the switch S is open?
b) Which point, a or b, is at higher potential?
Now the switch S is closed.
b) What is the final potential of point b?
c) How much charge flows through switch S
when it is closed?
Solution
a) With an open switch:
Q  CeqV  (2.00 106 F)(18.0 V)  3.60 10-5 C.
Also, there is a current in the left branch:
I  (18.0 V)/(6.00   3.00 )  2.00 A.
So V  V  V  Q / C  IR
ab
6 mF
6
6 mF
6 mF
3.00 mF
 (3.6 105 C)/(6.0 10-6 F) - (2.0 A)(6.0 )  -6.00 V.
b) Point b is at the higher potential.
c) If the switch is closed: Vb  Va  (2.00 A)(3.00 )  6.00 V.
d) New charges are: Q3  CV  (3.00 10 6 F)(6.0 V)  1.80 10-5 C.
Q6  CV  (6.00 10 6 F)(-12.0 V)  -7.2010-5 C.
 Q3  3.60 10 5 C - (1.80 10-5 C)  1.80 10-5 C.
Q6  3.60 10 5 C - (-7.20 10-5 C)  3.60 10-5 C.
The total charge flowing
through the switch is
5.40 x 10-5 C.