* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 5A - Polynomial Functions
Vincent's theorem wikipedia , lookup
Functional decomposition wikipedia , lookup
Large numbers wikipedia , lookup
History of logarithms wikipedia , lookup
Factorization wikipedia , lookup
History of the function concept wikipedia , lookup
Function (mathematics) wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Non-standard calculus wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Big O notation wikipedia , lookup
Function of several real variables wikipedia , lookup
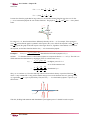
© : Pre-Calculus - Chapter 5A Chapter 5A - Polynomial Functions Definition of Polynomial Functions A polynomial function is any function px of the form px p n x n p n−1 x n−1 p 2 x 2 p 1 x p 0 , where all of the exponents are non-negative integers. The coefficients of the various powers of x, that is, the p i ’s are assumed to be known real numbers, and p n ≠ 0. The degree of this polynomial function is n. If n is even the polynomial is said to be of even degree and if n is odd, the polynomial is said to be of odd degree. The coefficient p 0 is called the constant term and the non-zero p n is called the leading coefficient. By a polynomial of degree 0, we mean a non-zero constant function. The zero polynomial function is sometimes said to have degree equal to − . In the table below we list a few polynomials and their degrees. polynomial degree constant term leading coefficient px 5 0 5 5 px 3x − 8 2 −8 3 px −6x x − 5x 9 5 9 −6 px 2x 126 126 0 2 2 5 4 We have studied two examples of polynomial functions already. Linear functions (fx mx b, m ≠ 0) are polynomial functions of degree 1, and quadratic functions (fx ax 2 bx c, a ≠ 0) are polynomial functions of degree 2. Below are some examples of polynomials of degree 3, 4, and 5. Example 1: Let px 5 − 6x 13x 3 . What is the degree of px? What are the leading coefficient and constant terms? Solution: The degree of px 5 − 6x − 13x 3 is 3. The largest exponent. The leading coefficient is −13 and the constant term is 5. Example 2: Let px 3x 4 − 3x 3 5x. What is the degree of px? What are the leading coefficient and constant terms? Solution: The degree of px 3x 4 − 3x 3 5x is 4. The leading coefficient is 3, and the constant term, the coefficient of x 0 , is 0. Example 3: If fx 16 − 3x 2 27x 4 − 5x 7 8x 13 , what are the degree, leading coefficient, and constant term equal to? Solution: The degree of fx 16 − 3x 2 27x 4 − 5x 7 8x 13 is 13. The leading coefficient is 8, and the constant term is 16. © : Pre-Calculus © : Pre-Calculus - Chapter 5A Behavior of Polynomial Functions In this page we will discuss how the values px of polynomial functions behave for large values of x, both positive and negative. It turns out that the behavior of polynomial functions for large values of x is determined by the degree of the polynomial. Polynomials of odd degree behave one way, think of the graph of a linear function, and polynomials of even degree behave in a different way, picture the graph of a quadratic function. Example 1: Solution: Plot the third degree polynomial x 3 . y x Notice that the function values of this polynomial as x goes to also go to , and as x goes to − the function values also go to − . Example 2: Solution: Plot the third degree polynomial −x 3 . y x Notice here that as x goes to the function values go to − . The reverse of the situation with x 3 . What is true, for both examples, is that as x gets large so to do the function values, and if one end of the graph goes up, the other end goes down. Example 3: Solution: Plot the fourth degree polynomial fx x 4 . y x Notice both ends of the graph get large in the same direction. Example 4: Solution: Plot the fourth degree polynomial fx −x 4 . y x Notice that both ends of the function get large in the same direction. © : Pre-Calculus © : Pre-Calculus - Chapter 5A What do you expect the graph of x 5 to look like? Question: Answer: The graph of x 5 is the graph of a polynomial of odd degree, so I would expect it (for large values of x) to look like the graph of x 3 or the graph of x. In the sense that if one end goes to plus infinity, then the other end goes to minus infinity. What do you expect the graph of x 16 to look like? Question: Answer: The graph of x 16 is the graph of a polynomial of even degree, so I would expect it (for large values of x) to look like the graph of x 4 or the graph of x 2 . In the sense that if one end goes to plus infinity, then the other end goes to plus infinity also. We summarize our findings: Theroem: Let px p 0 p 1 x p n x n be a polynomial of odd degree. If p n 0 , then as x goes to positive infinity px goes to positive infinity, and as x goes to negative infinity px goes to negative infinity If p n 0 , then as x goes to positive infinity px goes to negative infinity, and as x goes to negative infinity px goes to positive infinity Proof: The idea of the proof is fairly simple, we factor out the highest power of x in px, and notice how each factor must behave for large values of x. px p 0 p 1 x p n x n p1 p p x n n0 n−1 n−1 x pn x x Now if we examine each of the terms in the second factor we see that as x gets large either positively or negatively every one of the quotients must get smaller and smaller. That is every p term which of the form n−ii goes to zero as long as the exponent n − i is positive. So, for large x x the second factor gets closer and closer to p n , and for large x, px ≈ p n x n . Remember, n is an odd integer. If x goes to positve infinity, x n goes to positive infinity. Thus, if p n 0, px will go to positive infinity. If x goes to negatve infinity, then x n goes to negative infinity too, and if p n 0, then px will go to negative infinity. Remember that n is odd, so the sign of x n is the same as the sign of x. If p n 0, the situation is reversed. The way to remember this theorem is to remember what the graph of x 3 looks like compared to the graph of −x 3 . The leading coefficient of x 3 is positive and the leading coefficient of −x 3 is negative. © : Pre-Calculus © : Pre-Calculus - Chapter 5A Example 5: Show that as x goes to positive infinity the odd degree polynomial px 3 − x 2 5x 4 − 6x 9 goes to − . Solution: The theorem states that if the leading coefficient of an odd degree polynomial is negative, then as x goes to infinity the values of the polynomial go to negative infinity. The following calculation which parrots the above proof reinforces this. px 3 − x 2 5x 4 − 6x 9 x 9 39 − 17 55 − 6 . x x x Now as x goes to , the second factor goes to −6, which means that px, for large values of x, looks like −6x 9 . Thus, px must go to − as x goes to . Example 6: Show that as x goes to negative infinity the odd degree polynomial px 3 − x 2 5x 4 − 6x 9 goes to . Solution: The theorem states that if the leading coefficient of an odd degree polynomial is negative, then as x goes to negative infinity the polynomial values go to positive infinity. The following calculation which parrots the above proof reinforces this. px 3 − x 2 5x 4 − 6x 9 x 9 39 − 17 55 − 6 . x x x As x goes to − the second factor gets close to −6 just as in the previous example. Here though, as x goes to − the term x 9 also goes to − . Thus, the product of −6 and x 9 will go to positive infinity. Example 7: What will the graph of px 5 − x 3x 4 − 8x 7 look like for large values of x? Solution: px is an odd degree polynomial and its leading coefficient, −8, is negative. Thus as x goes to infinity, px will go to − , and as x goes to − , px will go to positive infinity. Theorem: Let px p 0 p 1 x p n x n be a polynomial of even degree. If p n 0 , then as x goes to positive infinity px goes to positive infinity, and as x goes to negative infinity px goes to positive infinity If p n 0 , then as x goes to positive infinity px goes to negative infinity, and as x goes to negative infinity px goes to negative infinity Proof: The idea of the proof is exactly the same as in the case where px is a polynomial of odd degree. px p 0 p 1 x p n x n p1 p p x n n0 n−1 n−1 x pn x x Now if we examine each of the terms in the second factor we see that as x gets large either positively or negatively every one of the quotients must get smaller and smaller. That is every © : Pre-Calculus © : Pre-Calculus - Chapter 5A p term which of the form n−ii goes to zero as long as the exponent n − i is positive. Thus, for x large x the second factor gets closer and closer to p n . Thus, for large x, px ≈ p n x n . So if x goes to plus infinity x n goes to plus plus infinity. Thus, if p n 0, px will go to plus infinity. If x goes to minus infinity, then x n goes to plus infinity, and if p n 0, then px will go to plus infinity. Remember that n is even, so the sign of x n is always positive. If p n 0, the situation is reversed. The way to remember this theorem is to remember what the graph of x 4 looks like compared to the graph of −x 4 . The leading coefficient of x 4 is positive and the leading coefficient of −x 4 is negative. Example 8: Describe what happens to the values of px −5 5x − 8x 3 − x 4 8x 10 as x goes to plus and minus infinity. Solution: The theorem states that for even degree polynomials if the leading coefficient is positive then the values of px must go to positive infinity for large values of x whether positive or negative. The following calculation parrots the above proof and is given here to reinforce these ideas. px −5 5x − 8x 3 − x 4 8x 10 x 10 − 510 59 − 87 − 16 8 . x x x x As x goes to infinity the second factor gets close to 8. Thus, px looks like 8x 10 , and as x gets large, positively or negatively, x 10 goes to positive infinity and so will 8x 10 . Example 9: What will the graph of px 9x 3 − 15x 16 look like for large values of x? Solution: This is an even degree polynomial whose leading coefficient (−15) is negative. Thus, from the theorem, as x goes to positive or negative infinity px goes to negative infinity. Let’s see what happens if we factor out x 16 . px 9x 3 − 15x 16 x 16 913 − 15 . x 9 As x gets large the term 13 gets smaller and smaller, so the second factor gets close to −15. Thus, for x large x, ps looks like −15x 16 , and as x gets large, either positively or negatively, −15x 16 goes to − . © : Pre-Calculus © : Pre-Calculus - Chapter 5A Exercises for Chapter 5A - Polynomial Functions 1. What is the constant term in the polynomial px 3x 4 − 5x 2 13 − 2x x 5 ? 2. What is the leading coefficient of −2x 3x 2 − 8 ? 3. If px is a polynomial of degree 2, with leading coefficient −3, constant term equal to 8, and p1 5, what is px? 4. Which of the following expressions is a polynomial? 4 a. x 2 − 3 b. −x 2 x c. x − 6x 2 d. 5x e. 5 x 5 − 83 5. What are the leading coefficient and constant term of px 4 − 5x 11x 2 7x 9 ? 6. What are the degrees of the following polynomials? a. 9x 3 5x 4 − 16x 2 b. 9x − 12 c. 22x 45 − 17x 23 − 1 d. 3x − 5 67x 5 x 4 7. Describe the behavior of x 3 for large values of x 8. If px is a polynomial of degree 5 and values of px go to as x goes to − , what happens to px for large positive values of x? 9. Can a polynomial px have the following properties: px is a polynomial whose leading coefficient is −2 and px goes to plus infinity as x gets large in either direction? © : Pre-Calculus © : Pre-Calculus - Chapter 5A Answers to Exercises for Chapter 5A - Polynomial Functions 1. 13 2. 3 3. We know that px −3x 2 bx 8. We also know that 5 p1 −3 b 8 b 5 . This implies that b 0, and hence, px −3x 2 8 . 4. Items a, c, and e are polynomials. 5. The leading coefficient is 7 and the constant term is 4. 6. a. 4 7. For large values of positive x the values of the polynomial x 3 get very large positively. For large negative values of x the polynomial x 3 also gets large in a negative sense. 8. The values of px go to − as x goes to . 9. No, since px behaves the same as x gets large in either direction, the degree of px must be even. But, if the leading coefficient of this polynomial is negative, then the polynomial’s values must go to minus infinity, not plus infinity. © b. 1 : Pre-Calculus c. 45 d. 5 © : Pre-Calculus - Chapter 5B Chapter 5B - Rational Functions Definition of a Rational Function In this page we define a rational function and look at some graphs of rational functions. Definition: A rational function is the quotient of two polynomials. That is, if rx is a px . rational function, then there are two polynomials px and qx such that rx qx − 5 . The quotient of px and If px 3x − 5 and qx x 2 − 2x, then rx 3x x 2 − 2x − 5 is shown below. Notice the behavior of rx for x qx, is a rational function of x. A plot of 3x x 2 − 2x close to 0 or 2. We say that the function has vertical asymptotes at x 0 and at x 2. Example 1: y x x=2 px . Since qx polynomials are defined for all x, the only real numbers which are not in the domain of any rational function are those values of x for which the denominator is zero. Thus, the domain of any rational px is the set of x for which qx ≠ 0. function qx The domain of a rational function is the set of real numbers x for which one can compute If we look at the rational function in the above example, its denominator equals x 2 − 2x xx − 2. Thus, the numbers x 0 and x 2 (The values for which the denominator equals zero.) are not in the − 5 , and all other values of x are in the domain. domain of the function 3x x 2 − 2x The x-intercepts of a rational function rx are those real numbers x for which rx 0. Note that a fraction can equal zero only if its numerator is zero. Thus, the x-intercepts are those values of x for which the numerator px 0. The y-intercept is that number y 0 such that r0 y 0 . Notice that there may be many x-intercepts, but there is at most one y-intercept. © : Pre-Calculus © : Pre-Calculus - Chapter 5B Question: When will there be no y-intercept? Answer: When 0 is not in the domain of the rational function. − 5 , x 0 is not in the domain of this rational function, hence In the previous example rx 3x x 2 − 2x there is no y-intercept. The x-intercept is x 5/3. Since that is the only value of x for which the numerator of rx is zero, there is only one x-intercept. Example 2: 2 Find the domain and intercepts of the rational function rx x −3 4x − 2 . x −1 Solution: To determine the domain we need to find those real numbers x for which x 3 − 1 0. The only solution to this equation is x 1. Thus, the domain consists of all real numbers except x 1. The y-intercept is r0 −2 2. The x-intercepts are those values of x for which x 2 − 4x − 2 0. −1 The solutions are x 2 6 and x 2 − 6 . A plot of this rational function is shown below. y x=1 x © : Pre-Calculus © : Pre-Calculus - Chapter 5B Horizontal Asymptotes There are times when we need to understand how a rational function behaves for very large (positive and negative) values of x. Before defining what a horizontal asymptote is we’ll look at the graphs of several rational functions. Example 1: Let rx 1x . Take note that the domain of this function is all non-zero x and it has no intercepts. We have plotted 1x below. Notice that for large values of x, either positive or negative, the function values get close to zero. We describe this phenomenon by saying that the line y 0 is a horizontal asymptote. y x 2 Let rx 2x 2− x 5 . Since the denominator is never zero, the domain is all real x 1 numbers. The y-intercept is the point 0, 5, and the x-intercepts are the solutions of the equation 2x 2 − x 5 0, which has no real solutions. (Use the quadratic formula.). Thus, there are no x-intercepts. An examination of a plot of this rational function shows that the line y 2 is a horizontal asymptote. Example 2: y y=2 x Notice that the graph crosses the horizontal asymptote. There is no truth to the idea that the graph of a function cannot cross a horizontal asymptote. In order to understand the concept of a horizontal asymptote we need to understand the idea of the limiting behavior of a function rx as x tends to plus or minus infinity. In the table below some values 2 of rx 2x 2− x 5 are shown for large values of positive and negative x. x 1 x −2 −20 −200 −2000 2 20 200 2000 rx 3 2. 0574 2. 0051 2. 0005 2. 2 1. 9576 1. 9951 1. 9995 This computation indicates that for large values of x, positive or negative, the function values of rx are getting close to 2. The following notation is used to indicate this. lim rx 2 and lim rx 2. x→ x→− These are read as ”The limit, as x goes to infinity, of rx equals 2” and ”The limit, as x goes to negative infinity, of rx equals 2” respectively. © : Pre-Calculus © : Pre-Calculus - Chapter 5B If you go on to take calculus, you will see this notation a lot. For now, just think of it as a shorthand to describe what happens to the values of a function as x gets large in either a positive or negative sense. The horizontal line y a is called a horizontal asymptote of the function rx if rx a, or if lim rx a. lim x→ x→− Determine the limit as x goes to infinity of 1x . Solution: We first make a table of values of 1x for large values of x. x 1 10 100 1, 000 10, 000 100, 000 10 n 1 1 . 1 . 01 . 001 . 0001 . 00001 10 −n x It seems clear that as x gets larger and larger the values of 1x get closer and closer to zero. Thus, we say 1 0. the limit of 1x as x goes to infinity is zero, and we write lim x→ x Example 3: Determine the domain, intercepts and horizontal asymptotes of rx 2x − 1 . x1 Solution: The domain consists of all x for which the denominator x 1 is not zero. Thus, the domain equals all x ≠ −1. The y-intercept equals r0 −1, and the x-intercept equals those x for which 2x − 1 0. That is, x 1 is the x-intercept. To find horizontal asymptotes we need to 2 determine if the values of rx approach a limiting value as x goes to plus or minus infinity. We construct a table of values to see if such is the case. Example 4: x 10 100 1000 10, 000 10 6 10 10 rx 1. 727 3 1. 970 3 1. 997 1. 999 7 2. 0 2. 0 These values indicate that lim rx 2. So we will have the line y 2 as a horizontal asymptote. A plot x→ of 2x − 1 is shown on the next page. x1 y y=2 x x= 1 Notice that rx approaches 2 as x goes to negative infinity as well. Any function of the form 1n where n is any positive integer goes to zero as x goes to x plus or minus infinity. That is, each of these functions has the line y 0 as an horizontal asymptote. To convince ourselves of this we plot several such functions for x 0, and then for x 0. The graphs of 13 , 14 , and 15 for x 0 are plotted below. x x x Example 5: 1 is in red x3 1 is in black x4 1 is in green x5 y (1, 1) x © : Pre-Calculus © : Pre-Calculus - Chapter 5B Notice that if 0 x 1, then 13 14 15 and x x x if 1 x, then 15 14 13 . x x x It seems clear from the graphs that for large values of x each of these rational functions gets close to 0. In fact y 0 is a horizontal asymptote for each of these functions. The graphs of 13 , 14 , and 15 for x 0 are plotted x x x below. 1 is in red x3 1 is in black x4 1 is in green x5 y ( 1, 1) x ( 1, 1) For values of x 0, these functions behave differently than they do for x 0. For example, if the exponent is even ( 14 in blue) then the graph is symmetric with respect to the y-axis, while if the exponent is odd ( 13 in red, x x and 15 in green) the graph is odd with respect to the origin. However, regardless of the oddness or evenness of x the exponent, each of these functions has the line y 0 as a horizontal asymptote. 3 2 Let rx −x 3 x 2 21x − 45 . Determine the horizontal asymptotes of rx. x − 3x − 6x 8 Solution: To determine if there is a horizontal asymptote we compute the limit as x → of rx. The trick is to divide numerator and denominator by the highest power of x which occurs in rx. 3 2 rx −x 3 x 2 21x − 45 the highest power of x is 3 x − 3x − 6x 8 so we divide numerator and −1 1x 212 − 453 x x denominator by x 3 . 1 − 3x − 62 83 x x Okay, we’ve rewritten rx. How does this help? The next observation is that any expression of the form cn x where c is any constant and n is any positive number must go to zero as the absolute value of x gets large. Thus, rx approaches −1 as x goes to plus infinity. Thus, the line y −1 is a horizontal asymptote. A plot of rx is 1 shown below. Example 6: y x y= 1 This trick, dividing both numerator and denominator by the highest power of x should be used everytime. © : Pre-Calculus © : Pre-Calculus - Chapter 5B px qx we need to be able to determine if the values of rx are approaching some number as x goes to positive or negative infinity. Fortunately, there is an easy way to determine what this limiting behavior is. This behavior is determined solely by the degrees of the polynomials px and qx. As we saw in the previous examples, to find horizontal asymptotes of a rational function rx Theorem: px be a rational function of x, where qx Let rx px p m x m p m−1 x m−1 p 0 and qx q n x n q n−1 x n−1 q 0 . m is the degree of px and n the degree of qx, then a. If m n (degree of denominator larger than degree of numerator) lim rx 0. x→ p b. If m n, (numerator and denominator have the same degree) then lim rx qmn . The ratio x→ of the coefficients of the largest powers of x. c. If m n, (degree of denominator smaller than degree of numerator) then rx has no limit as x tends to plus or minus infinity. In fact, the absolute value of rx becomes arbitrarily large. Example 7: Let rx 2x − 5 . Calculate the limit of rx as x goes to infinity. x2 x − 6 Solution: Since the degree of the numerator is 1, and this is less than 2 which is the degree of the denominator, we know that lim rx 0 x→ Example 8: 3 − 7x 15 . Calculate the limit of rx as x goes to infinity. Let rx −12x 3 3x x 2 x − 6 Solution: Since the degree of the numerator is 3, and this equals the degree of the denominator, we know that lim rx equals the ratio of the coefficients of the highest powers of x. Thus, x→ lim rx −12 −4. x→ 3 Example 9: Let rx 2x 3 − 5 . Calculate the limit of rx as x goes to infinity. x x−6 2 Solution: Since the degree of the numerator is 3, and this is larger than the degree of the denominator, the limit does not exist. © : Pre-Calculus © : Pre-Calculus - Chapter 5B Vertical Asymptotes In this page vertical asymptotes are defined and several examples are shown. If we look at a plot of the function 1x , we notice that as x gets close to zero the function values get larger and larger. In fact, the plot of this function in an interval about 0 looks like a vertical line going straight up (for x 0) and down (for x 0). We describe this phenomenon by saying that 1x has a vertical asymptote at x 0. Notice that the value of x for which this function has a vertical asymptote, x 0, is a point at which the denominator equals zero. This is the secret to locating vertical asymptotes. That is, look for those values of x for which the denominator equals 0. A little care has to be taken as we shall see in one of the examples below. Plot the function fx Example 1: 1 , and locate its vertical asymptotes. x2 Solution: Before plotting this function we notice that it is not defined at x −2, as that is where the denominator equals zero, and we suspect that there is a vertical asymptote at x −2. A plot of the graph of fx is shown below. Note that as x gets close to −2, the function values get large in either a positive or a negative sense. A plot of 1 x+2 -2 1 . Construct a table of values of fx for x close to −2. x2 Let fx Example 2: Solution: x −2. 1 −2. 01 −2. 001 −2. 0001 −1. 9999 −1. 999 −1. 99 −1. 9 fx −10. 0 −100. 0 −1, 000. 0 −10, 000. 0 10, 000. 0 1, 000. 0 100. 0 10. 0 Notice that the closer x gets to −2 the absolute value of fx becomes larger. As x gets close to −2 from above, i.e., x is larger than −2, the numbers fx get arbitrarily large ( lim fx ). x→−2 As x gets close to −2 from below, i.e., x is smaller than −2, the numbers fx get arbitrarily large in a negative sense ( lim − fx −). x→−2 The above calculations indicate that the function © : Pre-Calculus 1 has a vertical asymptote at x −2. x2 © : Pre-Calculus - Chapter 5B Plot the function fx x2 − 1 , and locate its vertical asymptotes. x −1 Solution: The denominator of this rational function is zero at x 1 and x −1. From the previous examples we suspect that there are vertical asymptotes at both of these values. However, we are wrong, there is no vertical asymptote at x 1. The numerator is also zero at x 1, which cancels the zero in the denominator. A plot of this function appears below. Notice there is only one place where the function values get larger and larger; that is, at x −1. Example 3: A plot of x-1 x 2 -1 -1 The open circle at the point (1,1/2) indicates that this point is not on the graph of the function. Remember that x =1 is not in the domain. We know how to spot a vertical asymptote from a graph (wherever the plotted values get arbitrary large). We next give an analytical definition of a vertical asymptote. Definition: We say a function y fx has a vertical asymptote at x a if the numbers |fx| get arbitrarily large as x approaches the value a from the right or the left. In the language of calculus we say that the limit as x approaches a from above or below is infinite and write lim fx or x→a− lim fx respectively. x→a The fact that the function values must become infinite is why x 1 is not a vertical asymptote in the last example. To explore this further read the examples below. In summary, to find a vertical asymptote for a rational function px do the following: qx px in lowest terms. That is, cancel all common factors. qx px If is in lowest terms, this rational function will have a vertical asysmptote at all values of qx px will be the locations of x for which qx 0. That is, all values of x not in the domain of qx vertical asymptotes. Put x , and locate its vertical asymptotes. x 3x − 4 Solution: We notice that the denominator of this function is zero at the points x −3 and at x 4, which leads us to believe that there are two vertical asymptotes. One at each of the values −3 and 4. Example 4: Plot the function fx A plot of -3 © : Pre-Calculus 1 (x+3)(x-4) 4 © : Pre-Calculus - Chapter 5B Let fx x2 − 1 . Show by constructing tables of values that this function has a x −1 vertical asymptote at x −1 and does not have a vertical asymptote at x 1. Solution: We look at values of x close to −1 first. Example 5: x −1. 1 −1. 01 −1. 001 −1. 0001 −. 9 −. 99 −. 999 −. 9999 fx −10. 0 −100. 0 −1, 000. 0 −10, 000. 0 10. 0 100. 0 1, 000. 0 10, 000. 0 We notice that the function values are getting arbitrarily large as x gets close to −1, and conclude that x −1 is a vertical asymptote. The following table shows the values of fx for x close to 1. x 1. 1 1. 01 1. 001 1. 0001 0. 9 0. 99 0. 999 0. 9999 fx . 476 19 . 497 51 . 499 75 . 499 98 . 526 32 . 502 51 . 500 25 . 500 03 In this case the function values are getting closer and closer to 1 as x approaches 1. In fact, if we 2 rewrite this function as fx x2 − 1 1 , we see that as x approaches 1, x 1 approaches 2, and x1 x −1 1 its reciprocal, which is fx, approaches . 2 We now examine what happens to vertical and horizontal asymptotes of the function 1x as it undergoes various transformations. As a reminder the domain of 1x is all real numbers except x 0, its range is all real numbers y ≠ 0, and it has a horizontal asymptote at y 0, and a vertical asymptote at x 0. Example 6: Translate fx 1x two units to the right. Determine the domain, range, and all horizontal and vertical asymptotes. Plot the function. Solution: The function rx 1 is the translate of 1x two units to the right. To find the x−2 horizontal asymptote we note that as x approaches the function values of rx approach 0. We also see that rx is in lowest terms, and that its denominator equals 0 when x 2. Thus, x 2 is a vertical asymptote. We summarize these remarks in the table below. A plot of Domain all x ≠ 2 Range all y ≠ 0 Horizontal Asymptote y0 Vertical asymptote x2 1 is shown below. x−2 y 2 © : Pre-Calculus x © : Pre-Calculus - Chapter 5B Example 7: Translate fx 1x three units down. Determine the range, domain, and all asymptotes. Solution: The function rx 1x − 3 is the downward translation of 1x by three units. The domain, range, and asymptotes are tabulated below. Domain all x ≠ 0 Range all y ≠ −3 Vertical Asymptote x0 Horizontal Asymptote y −3 A plot of rx follows y x y = -3 The table below lists the domain, range and asymptotes of 1x under general horizontal and vertical transformations. Domain Range Vertical Asymptote Horizontal Asymptote 1 xa y0 x − a all x ≠ a all y ≠ 0 1 − a all x ≠ 0 all y ≠ −a x0 y −a x 1 . Determine the domain, range, and asymptotes of this function. x−5 Solution: The domain consists of all x ≠ 5. We note that if x 5, then fx 0 and if x 5, then fx 0, and that we have a vertical asymptote at x 5. Moreover from the sign of fx we expect that as x approaches 5 through values of x 5, that fx will approach − , and as x approaches 5 through values of x 5, that fx will approach . Example 8: Let fx A table of function values for x close to 5 is displayed below. x 4. 9 4. 99 4. 999 5. 001 5. 01 5. 1 fx −10. 0 −100. 0 −1000. 0 1000. 0 100. 0 10. 0 This function has a vertical asymptote at x 5 and a horizontal asymptote at y 0. Its domain is all x ≠ 5 and its range is all y ≠ 0. A graph of 1 is shown below. x−5 y 5 x Notice that the graph of fx is the graph of 1x shifted to the right by 5 units. © : Pre-Calculus © : Pre-Calculus - Chapter 5B Example 9: Let fx 1 1. What are the range, domain, and asymptotes of this function? x−3 Solution: The only real number x which cannot be evaluated by f is x 3. For if we try to compute f3 we first compute 3 − 3, this equals 0, but then we have to take the reciprical of 0, which is not possible. Thus, the domain is all real numbers except 3. The range equals all y such that for some x ≠ 3 we have y 1 1 x−3 y−1 1 x−3 1 x−3 y−1 x 1 3 y−1 The only value of y for which the above computation is not possible is y 1. Thus, the range of fx is all y ≠ 1. The vertical asymptote is x 3 and the horizontal asymptote is y 1. A plot of fx is shown below: y y=1 x=3 x Notice that the graph of fx is obtained from the graph of 1x by shifting to the right 3 units and up 1 unit. © : Pre-Calculus © : Pre-Calculus - Chapter 5B Exercises for Chapter 5B - Rational Functions 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. © Which of the following functions is rational? 3 2 c. x x x − 3 d. x 2 − 3x 5 a. 2x, b. 4 x − 1 2 x 2x − 5 x − 1 Is fx a rational function. x Find the domain of each of the following functions. x−1 a. x2 − 1 3 b. 2x −3 5x 8 x −8 5 −1 x c. x2 x − 2 Find the range of the following functions. 1 a. x−2 1 −1 b. x2 c. 3 − 2 x5 In problems 5 through 9 find the x and y-intercepts of the rational function: 2x − 6 x2 1 x2 − 4 2x x 2x 1 3 x1 x 2 − 3x − 4 2x Find the limit as x → of 2x x− 1 2 Find the limit as x → of 2x x− 1 2 Find the horizontal asymptote of rx 2x 2 − 6 and plot the function −x 2 3 2 Find the limit as x → of x − x 4 5x − 18 , and plot the function for large values of x 19x 15 2 x − 2x 7 Does the function have a horizontal asymptote? x−1 Find a rational function which has the line y 6 as a horizontal asymptote. Find a rational function which has 2 as an x-intercept and the line y −1 as a horizontal asymptote. Find a rational function which has −3 as an x-intercept, 7 as a y-intercept, and has the line y 1 as a horizontal asymptote. For each of the following functions locate their vertical asymptotes, and then plot the functions. x a. x−1 x2 − 2 b. 2 x − 3x 2 x−1 c. x 2 2x − 3 : Pre-Calculus © : Pre-Calculus - Chapter 5B 2x 2 − 1 x2 − x − 6 2 Locate all vertical and horizontal asymptotes of y x − 1 2x 3 2 Find all intercepts and asymptotes of the function y x 2− 4 −3x 27 2 3x − 1 Find all asymptotes of the function y 3 x −1 4 x − x 3 − 4x 7 Find all asymptotes of the function y 5x 2 − 6 Find a rational function which has y 1 as a horizontal asymptote and the lines x 3 and x 5 as vertical asymptotes Find a rational function which has the line y 5 as a horizontal asymptote and the lines 2 x 4, x 5, and x −2 as vertical asymptotes 2 2 Determine the horizontal and vertical asymptotes for fx ax 2 − ab2 cd − cx 19. Locate all vertical and horizontal asymptotes of y 20. 21. 22. 23. 24. 25. 26. © : Pre-Calculus © : Pre-Calculus - Chapter 5B Answers to Exercises for Chapter 5B - Rational Functions 1. 2. 3. The first two and the last function are rational, the third one is not. 2 x is not a polynomial in x. No, the denomiator x is not a polynomial in x. a. All x such that x 2 − 1 ≠ 0. That is, x ≠ 1. b. All x such that x 3 − 8 is not zero. Thus, all x ≠ 2. c. All x such that x 2 x − 2 x − 1x 2 ≠ 0. Thus, all x not equal to 1 or −2. 4. Find the range of the following functions. a. All y ≠ 0. b. Range is all y −1. For if y 12 − 1 y 1 12 x 2 1 This is y1 x x possible if y ≠ −1. x 1 This is possible if y 1 0. Thus, there is y1 an x in the domain of fx as long as y −1. Another line of reasoning is as follows. The range of the function 12 is all positive numbers. Hence, the range x of 12 − 1 must be all numbers larger than −1. x c. y 3 − 2 y − 3 − 2 x 5 2 x 2 − 5. Thus, the x5 x5 3−y 3−y range of fx 3 − 2 is all y ≠ 3. x5 5. The x-intercept is x 3, and the y-intercept is y −6. 2 6. The x-intercepts are x 2. There is no y-intercept, since 0 is not in the domain of x − 4 . 2x 7. x 0 is the x-intercept, and y 0 is the y-intercept. 8. There is no x-intercept, and the y-intercept is 3. 9. There are two x-intercepts, x −1 and x 4. There is no y-intercept since 0 is not in the domain of the function. 10. 2 11. If we carry out the division we rewrite the function as 2x − 1x . As x goes to infinity the 1x term goes to zero and the 2x term becomes infinite. We say in this case that the limit does not exist. 2x 2 − 6 −2, the line y −2 is a horizontal asymptote. 12. Since lim x→ −x 2 2 y x 3 y= 2 13. The denominator has degree larger than the numerator. Thus, the function goes to zero as x goes to infinity. y x © : Pre-Calculus © : Pre-Calculus - Chapter 5B 14. No the values of the function become unbounded as x goes to plus or minus infinity. Note that the degree of the numerator is larger than the degree of the denominator. 15. The are an infinite number of such rational functions. Three of them are y 6, 3 2 and y 6x −3 5x − x − 8 y 12x − 8 , 2x 5 x 2x − 4 x is one such rational function. There are of course many rational functions which fit 16. 2 − x the bill. 7x 3 17. One solution is y . One way to find such functions is to look for a solution of the 7x 3 ax b form y . Then the criteria that y must satisfy impose conditions on the coefficients cx d criteria condition −3 an x-intercept −3a b 0 b 7 7 the y-intercept d a 1 1 the horizontal symptote c of the rational function, and they are: These conditions are a system of three equations in four unknowns. The system is −3a b 0 b − 7d 0 a−c 0 One solution to this system is d 3, c 7, b 21, and a 7. 18. a. x1 y y=1 x x =1 b. The denominator factors into x 2 − 3x 2 x − 1x − 2. Since the zeros in the denominator are not cancelled by corresponding zeros in the numerator, we have the lines x 1 and x 2 as vertical asymptotes. y x=1 x x=2 c. x−1 x−1 1 if x ≠ 1. Thus, only the line x −3 is a x3 x 3x − 1 x 2 2x − 3 vertical asymptote y x x= 3 19. Since the degrees of the numerator and denominator are the same, there is a horizontal asymptote and it equals the ratio of the coefficients of the largest powers of x. In this case that ratio equals 2. Thus, y 2 is a horizontal symptote. The denominator factors into © : Pre-Calculus © : Pre-Calculus - Chapter 5B x 2 − x − 6 x − 3x 2. Thus the vertical lines x 3 and x −2 are vertical asymptotes. 20. Since the degree of the numerator is larger than the degree of the denominator, there is no horizontal asymptote. There is a vertical asymptote at x −3 . 2 21. x-intercepts: x 2. y-intercept: y −4 . vertical asymptotes at x 3. horizontal 27 asymptote y −1 . The function is plotted below. 3 y x= 3 x=3 x y = 1/3 22. horizontal asymptote: y 0 23. horizontal asymptote: none x2 x − 3x − 5 5x 3 25. y 2x − 4x − 5x 2 a 26. horizontal asymptote: y −c does not equal |d| ) vertical asymptote: x 1 vertical asymptote: x 6 5 24. y © : Pre-Calculus vertical asymptotes: x −d, x d (Note: As long as |b| © : Pre-Calculus - Chapter 5C Chapter 5C - Exponential Functions Review of Exponents In this chapter we will define and discuss the properties of exponential functions. These are functions of the form a x where a is a positive real number, and x is any real number. Before discussing this function, we’ll quickly review the laws of exponents, and then show how a x is defined for irrational numbers. A reminder of terminology: a is called the base and x is called the power or exponent. Below we quickly review exponentiation, and the laws of exponents. For a more thorough review see the previous chapter on Exponents. The following lists those x for which we can compute a x , and how to do so. Remember a is any positive real number. 1. 2. 3. 4. 5. If x 0, then a x is defined to be 1. If x is a positive integer, then a x is computed by multiplying a by itself x times. Thus, a 5 aaaaa −x 5 . Thus, a −5 1 If x is a negative integer, then a x 1 a a . If x is the reciprocal of an integer, e.g., x 1 , then a x b where b 1/x a. Note: if x 1/5, 5 then 1/x 5. Thus, a 1/5 b, if and only if b 5 a. That is, a x is the x th root of a. There is of course a computational problem here. It may not be easy to compute the x th root of a. x m 1/n If x is a rational number, i.e., x m n where m and n ≠ 0 are integers, then a a . The table below lists the algebraic properties of exponents: 1 a m a n a mn m 2 a n a m−n a 3 a −n 1n a 0 4 a 1 for a ≠ 0 5 ab n a n b n a n an 6 b bn n 7 a m a mn If you don’t already have these rules memorized, stop right now, and memorize them. © : Pre-Calculus © : Pre-Calculus - Chapter 5C What does 16 −3/4 equal? Question: Answer: 16 −3/4 2 4 −3/4 2 −3 8 −1 1 8 x The problem we now face is what does a mean if x is an irrational number? For example what do 2 , or 3 2 equal? See the next page for a discussion of this. In this page the computation of a x is discussed for the case when x is irrational. We need one property of rational numbers before we can compute a x , and this property is: Given any irrational number x, there is a rational number m n which is as close to x as we want. Another way to express this, is to say that any irrational number can be approximated as closely as we desire with a rational number. This is the key to calculating (approximating) a x , we find a rational number m n which is m/n m/n very close to x, and then compute a . This number, a , can then be shown to be close to something. This something is called a x . The plot below shows 2 x for various rational values of x between −1 and 1, they are the red circles. The blue curve is the plot of 2 x on the interval −1 to 1. y 2 (0.5, 1.414) 1 ( 0.5 , 0.707) 1 0.5 0 0.5 1 x There are only a few red dots and lots of blue. This is the general situation. There are a lot more irrational numbers then there are rational numbers, but the amazing thing is that any irrational number can be approximated with a rational number. In the following example we use a calculator to compute 2 x for a sequence of rational numbers x which are getting close to the irrational number 2 . These numbers 2 x will be getting close to 2 2 . Example 1: Compute 2 x for a sequence of x’s getting close to 2 . Solution: The rational numbers we will use to approximate 2 are 1. 4, 1. 41, 1. 414, 1. 414 2, 1. 414 21, and finally 1. 414 213. The table below list these values of x and below them the corresponding values of 2 x . x 2 The value of 2 2 x 1. 4 1. 41 1. 414 1. 4142 1. 41421 1. 414213 2. 63902 2. 65737 2. 66475 2. 66512 2. 66514 2. 66514 as computed by our calculator to 7 decimal places is 2 2 2. 665144 1 Just imagine how long it would have taken to compute 2 1.414 with out the aid of our calculator, and even then we are only within 2 decimal place accuracy of 2 2 . © : Pre-Calculus © : Pre-Calculus - Chapter 5C We list one more time the laws of exponents. This time with the remark that the powers are now allowed to be any real number. 1. 2. 3. 4. 5. 6. 7. © For any positive real number a, and any real numbers x and y, the following properties hold: a x a y a xy a x a x−y ay a −x 1x a a 0 1 for a ≠ 0 ab x a x b x a x ax b bx x y xy a a : Pre-Calculus © : Pre-Calculus - Chapter 5C Exponential Functions In this page we discuss the behavior of the exponential functions y a x . It turns out that there are three different modes of behavior: one if a satisfies 0 a 1, a different mode for a’s which satisfy 1 a, the third type of behavior occurs when a equals 1. We formally define what we mean by the exponential function with base a. Definition: The function fx a x , with 0 a and x any real number, is called the exponential function with base a. x 1 2 In the table below we list values of x fx 1 gx 2 x 2 and 2 x for various values of x, and then plot both functions. x −3 −2 −1 0 1/2 x 2x 1 2 3 1 4 1 8 4 8 8 4 2 1 1 2 1 8 1 4 1 2 2 1 There are several items to notice from this table of data. 0 1. 2 0 1 1. This is of course true for any positive a. We always have a 0 1. 2 −x for any x. Note: that this is also true for any positive a. 2. 2 x 1 2 These facts are true for any base a but deserve to be repeated for what they will imply about the graphs x of the two functions y a x and y 1 a . The plot below demonstrates this more clearly than words can. y 2 x y=1 x x 1 and 2 x . 2 are the reflections of each other through the y-axis. Plots of The plots of 2 x and 1 2 x Example 1: If the point 2, 36 is on the graph of a x , what must a equal? Solution: The statement that 2, 36 is on the graph of a x means that a 2 36. Thus, a 36 6. Question: Answer: © If 3 x 81, what must x equal? 4. 3 4 3 2 2 9 2 81 : Pre-Calculus © : Pre-Calculus - Chapter 5C 1 x on the same graph. 3 A table of values is first constructed. The two plots follow the table. Plot the functions y 3 x and y Example 2: Solution: −2 −1 0 1 1 1 9 3 x 3x 1 3 x 9 3 1 1 2 3 3 9 27 1 3 1 9 1 27 y 3 x y=1 x Notice that as with 2 x and x 1 2 the plots are the reflections of each other through the y-axis. Example 3: Using technology fill in the following table of values. Then plot these values and connect the dots to get an approximation to the graph of 4 x . x −2 −1. 5 −1 −0. 5 0. 5 1 1. 5 2 4x Solution: x 4 x −2 −1. 5 −1 −0. 5 0. 5 1 1. 5 . 0 625 . 125 1 4 2 0. 5 2. 0 4 8. 0 16 16 8 4 2 0.5 1 1.5 2 We continue our discussion of the behavior of the exponential functions y a x . We saw in the last x behave differently. Below we characterize this behavior in terms of the page that y 2 x and y 1 2 x size of the base of a . © : Pre-Calculus © 1. : Pre-Calculus - Chapter 5C If a 1, then the graph of a x looks like the graph of 2 x . That is, y 2 x x Note: see property 5. below. 2. If 0 a 1, then the graph of a x looks like the graph of 1 2 x . That is, y 1 2 x x 3. Note: see property 6. below. If a 1, then the graph of a x is the horizontal line y 1. y 1 x Below is a list of the properties of these exponential functions. 1. 2. 3. 4. 5. 6. The domain of fx a x is all real numbers. The range of fx a x , if a ≠ 1, is all positive real numbers. If a 1, then the range is the set consisting of the number 1 only. Note: a x can never equal 0. If a 1, then fx a x goes to infinity as x goes to infinity, and fx a x goes to zero as x goes to minus infinity. If 0 a 1, then fx a x goes to zero as x goes to infinity, and fx a x goes to infinity as x goes to minus infinity. If 1 a and x y, then a x a y . fx a x is an increasing function if a 1. If 0 a 1 and x y, then a x a y . fx a x is a decreasing function if 0 a 1. Memorize these properties. © : Pre-Calculus © : Pre-Calculus - Chapter 5C 6 5 Which number is bigger 1 or 1 ? 3 3 Solution: Since a 1 is less than 1, property 6. above tells us that the larger the exponent is 3 5 6 is larger than 1 . the smaller the value of the exponential function. Thus, the number 1 3 3 Example 4: Example 5: What does the plot of 2 2 x look like compared to the plot of 2 x ? Solution: There are two ways to answer this. One is to say that the plot of 2 2 x is just the plot of 2 x magnified along the vertical axis by a factor of 2. A perhaps better description is to use the following law of exponents 2 2 x 2 1 2 x 2 x1 . This tells us that the graph of 2 2 x is the translate by one unit along the x-axis of the graph of 2 x . Both graphs are shown below. y 2 x+1 2 x x We now compare the graphs and related properties of exponential functions with different bases. Below are plots of y 1. 5 x , y 2 x , y 2. 5 x , y 3 x and y 3. 5 x for −1 ≤ x ≤ 1. a = 3.5 3.5 a=3 3 a = 2.5 2.5 a=2 2 a = 1.5 1.5 1 0.5 -1 -0.5 0 0.5 y = a x for 1 < a x 1 The next plot compares the graphs of y a x for different values of a less than 1. In particular a 0. 25, 0. 5, and 0. 75 for −1 ≤ x ≤ 1. 0.25 x 4 3.5 3 0.5 x 2.5 0.75 x 1.5 2 1 0.5 -1 -0.5 0 0.5 x 1 y = ax for 0 < a < 1 From these graphs we summarize how the values of a x compare to each other. If a b and x 0, then a x b x . If a b and x 0, then a x b x . © : Pre-Calculus © : Pre-Calculus - Chapter 5C Example 6: Which number is larger 2 − 2 or 3 − 2 ? Solution: With the above rules in mind we observe that 2 3, and that the exponents are the same and negative. Thus, 2 − 2 is bigger than 3 − 2 . To reassure ourselves we use a calculator to compute approximations to these numbers. 2 − 2 ≈ . 375 214 23 3− 2 . 211 469 94 . Example 7: Let fx 2 x . Plot the vertical shift of the graph of fx which is given by fx 3. Solution: This vertical shift displaces the graph of 2 x three units upwards. y x y=2 +3 4 y=3 1 x 0 The domain of 2 x is all real numbers and its range is all positive real numbers. The domain of 2 x 3 is also all real numbers, however its domain is all numbers greater than 3. Example 8: Let fx 2 x . Plot the horizontal translate fx 1 2 x1 of fx. Solution: This horizontal shift displaces the graph of fx 2 x one unit to the left. y y=2 x+1 2 1 0 x The domain and range of 2 x1 are the same as the domain and range of 2 x . Domain of 2 x1 is all real numbers, and the range of 2 x1 is all positive real numbers. © : Pre-Calculus © : Pre-Calculus - Chapter 5C The Natural Exponential Function For every positive number a there is a corresponding exponential function. From all of these many exponential functions there is one which is called the natural exponential function. Its base is denoted by the letter e to distinguish it from all of the other bases. In the following we discuss the number e, and why e x is the most commonly used exponential function. For reasons discussed later the number e is calculated by computing 1 1 n values of n. In the language of calculus e is defined to be the limit of 1 1 n infinity. n for large n as n goes to n In the table below the values of 1 1n are shown for various n. n 10 100 1000 10, 000 n 1 1 2. 5937425 2. 7048138 2. 7169239 2. 7181459 n It seems as though the value of this number e is approximately 2. 71. A better approximation to e is e ≈ 2. 71828182845905 . It can be shown that the number e is not only an irrational number, but is also a transcendental number. A number c is said to be algebraic if there is a polynomial px with integer coefficients such that pc 0. If the number c is not algebraic, it is said to be transcendental. Clearly, if only pencil and paper were available to compute e x , the computation would take a long time. Fortunately calculators can rapidly and accurately compute these numbers. The number e lies between 2 and 3. Thus, e x lies between 2 x and 3 x . The plots of these three exponential functions are shown below. y 3x ex 2x x Example 1: Compute e x for x −3, −2, −1, 0, 1, 2, and 3. Solution: e −3 4. 97871 10 −2 , e −2 0. 135335, e 1 2. 71828, e 2 7. 38906, e 3 20. 0855 Question: e −1 . 367879, e 0 1. 0 Place the following numbers in increasing order. 2. 79 5 , 2. 78 5 , and e 5 . Answer: e 5 , 2. 78 5 , 2. 79 5 . The number e is approximately 2. 71. Thus, e 2. 78 2. 79 and raising these numbers to the fifth power preserves the inequalities. © : Pre-Calculus © : Pre-Calculus - Chapter 5C n n 1 1 , where nlim 1 1 represents the unique We saw in the previous page that e nlim n n → → n number which the terms 1 1n get closer and closer to as n gets larger and larger. We will use this formula to get a similar formula for e x . n is close to e. Therefore the number For large n the number 1 1 n x e . We now manipulate this latter expression. n x nx ex ≈ 1 1 1 1 let y nx n n 1 xy y 1 nx n 1 1 n n x should be close to now replace y with n . Note that if x 0, then y goes to if and if n goes to . This gives us the formula e x nlim 1 nx → n . Notice that if x 1, we have the original formula for e. The argument used to derive this formula is not a proof, there are too many missing steps. Think of it as an heuristic reason for believing that the formula is true. If you want to see a real proof of this formula, calculus is where to go. Example 2: Solution: n Use the formula e x nlim 1 nx to find an approximation to the number e 3.1 . → n for n 100, 1000, and 10, 000. We use our calculator to compute 1 3.n1 The value of e 3.1 Example 3: Solution: values. n 100 1000 10, 000 n 1 3.n1 21. 1771 22. 0918 22. 1873 computed by our calculator is e 3.1 22. 197951 . n Use the formula e x nlim 1 nx to approximate e −1 . → The table below contains values of the expression 1 −1 n n 1 −1 n 1000 n 10, 000 100, 000 n for n equal to various 1, 000, 000 . 36769542 . 36786105 . 3678776 . 36787926 We should feel comfortable using the value 0. 36787926 obtained with n 1, 000, 000. The actual value of e −1 to 8 places is e −1 ≈ 0. 36787944 © : Pre-Calculus © : Pre-Calculus - Chapter 5C Exercises for Chapter 5C - Exponential Functions 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 3 Simplify 242 6 Simplify the expression 4 2 8 −3 15 2 3 −4 Simplify 2 4 2 −3 5 If a x 16, what is a x/2 ? If a 3 27, what is a ? If a 2 5 and b 4 81, what does ab 8 equal? If a 3 7 and b −3 5, what does a 2 b 3 equal ? Evaluate the function fx 2 x at 10 different values of x and plot the ordered pairs x, fx. Evaluate the function fx 0. 9 x at 10 different values of x and plot the ordered pairs x, fx x Evaluate the function fx 1 and fx 1 at 10 different values of x. Then plot both 3 sets of data on the same graph. That is, if you’ve calculated f2 and f2 1 plot the ordered pairs 2, f2 and 2, f2 1. Graph the two functions fx 4 x and gx 4. 5 x on the same plot. Before doing so with your graphing calculator sketch the two graphs using pencil and paper paying particular attention to which one lies below the other. Which gets bigger faster 2 x or x 2 as x goes to infinity ? Use graphs to answer this. Plot on the same graph the two functions fx 1. 5 x and gx 1. 5 x 2. Which gets bigger faster 2 x or x 3 as x goes to infinity ? Compute the values of both functions for several values of x to try and decide the answer to this question. Which gets bigger faster 2 x or x 10 as x goes to infinity ? Compute the values of both functions for several values of x to try and decide the answer to this question. Note: it can be shown that no matter what n equals, the function 2 x will eventually get larger than x n . The plots of the three functions 3 −x , 2 x−1 , and 4 x are shown below. Which plot belongs to which function ? a. | 2 | 1 10 | 5 | | y 15 | 0 | 1 | 2 x | 2 c. © : Pre-Calculus | 1 4 | 2 | 6 | b. | 0 : Pre-Calculus - Chapter 5C | 4 4 | 2 | 6 | © | 2 | 0 17. The graph of a function of the form ka x is shown below. From the graph determine k and a (2, 45) 5 18. If e x 3 and e y 7, what does e xy equal ? n 1 nx to approximate e 3 by taking n 50, 000. Then compare 19. Use the formula e x nlim → this approximate value with what your calculator says e 3 equals. 20. If e x 5, what does e 2x equal ? 21. The number e lies between 2 and 3. Between what two numbers must e 5 lie ? 22. The natural number e’s decimal approximation to 5 places is e ≈ 2. 718 28. If we set a 2. 718 28, then a e, and if x 0 we have a x e x . What does e 5 − a 5 equal ? 23. The number e satisfies 2. 7 e 2. 8. Using this inequality what can you say about the number e −1 ? 24. Solve for x: 8 2x−1 16 x5 © : Pre-Calculus © : Pre-Calculus - Chapter 5C Answers to Exercises for Chapter 5C - Exponential Functions 1. 2. 3. 4. 5. 6. 7. 3 24 3 4 6 4 3 6 3 4 3 6 384 62 62 62 2 2 2 2 2 2 4 2 3 5 2 4 2 8 −3 15 2 3 −4 4 3154 3 3 4 4 5 3 35 2 25 3 4 288 8 3 2 3 4 2 3 4 2 4 3 4 −3 5 4−3 5 1 5 5 2 2 2 2 2 32 a x/2 a x 1/2 16 1/2 4 a a 3 1/3 27 1/3 3 2 2 5 2 81 5 4 81 2 4, 100 , 625. One could also ab 8 a 4 b 4 2 a 2 2 b 4 8 realize that a 5 1/2 and b 81 1/4 . Thus, ab 8 5 1/2 81 1/4 5 4 81 2 . 2 a 2 b 3 a 3 2 b −3 −1 7 2 5 −1 7 49 5 5 8. y ( 1, (2, 4) ) x 9. y ( 1, 1.111) (1, 0.9) x 10. y (0, 1) (0, 1/3) x 11. Since 4 4. 5, the graph of 4 x will lie below the graph of 4. 5 x for x 0 and above it for x 0. 4.5x 2 4x 1 0.6 -0.4 -0.2 0 0.2 0.4 x 12. 2 gets bigger faster than x 2 as is shown in the plot below. 2x 60 40 x 20 0 © 2 4 : Pre-Calculus 6 2 © : Pre-Calculus - Chapter 5C 13. y 3 1 x x 14. 2 x 2 4 8 16 4. 0 16. 0 256. 0 65, 536. 0 x 3 8. 0 64. 0 512. 0 4, 096. 0 From this table it appears that 2 x gets bigger faster than x 3 even though x 3 is bigger for smaller values of x. 15. x 2 4 8 16 2x 4 16 256 65, 536. 0 32 64 128 4. 29497 10 9 1. 84467 10 19 3. 40282 10 38 x 10 1024 1, 048, 576 1. 07374 10 9 1. 09951 10 12 1. 12590 10 15 1. 152 92 10 18 1. 18059 10 21 From this table it appears that 2 x gets bigger faster than x 10 even though x 10 is bigger for smaller values of x. 16. a. is 4 x , b. is 3 −x , and c. is 2 x−1 17. Since the graph passes through the point 0, 5 we must have k 5. The other data point 2, 45 then gives us the equation 45 5a 2 9 a2 3 a. 18. e xy e x e y 3 7 21 n 19. From the formula e x nlim 1 nx , we have e 3 nlim 1 3 n → → n expression 1 3 at n 50, 000, we have n e 3 ≈ 20. 083 729 Using our calculator we have e 3 ≈ 20. 085 537 . 20. e 2x e x 2 5 2 25 21. e 5 must satisfy the inequality 2 5 e 5 3 5 or 32 e 5 243 © : Pre-Calculus n . Evaluating the © : Pre-Calculus - Chapter 5C 22. e 5 − 2. 718 28 5 148. 413 159 102 577 − 148. 412 659 950 842 . 000 499 151 735 23. From 2. 7 e 2. 8 we have 1 1 1 e 2. 8 2. 7 1 . 357 142 8 e . 370 370 3 Remember too, that 1e e −1 . 24. 8 2x−1 16 x5 2 3 2x−1 2 4 x5 2 6x−3 2 4x20 Thus, 6x − 3 4x 20 2x 23 x 23/2 © : Pre-Calculus © : Pre-Calculus - Chapter 5D Chapter 5D - Logarithmic Functions Definition of Logarithms Logarithms were the invention of John Napier, a Scotsman, who invented them in the early 1600’s. Before the advent of computers these functions provided a means of easily performing many tedius computations. In fact, if you look at any mathematics text book more than 10 years old more than likely a table of logarithms will be in the back of the book. However, while it is true that logarithms are no longer needed for computations they still serve as a valuable tool in mathematics and science. In particular they are useful in solving equations which contain exponential functions. Logarithms are difficult for students to master. More than likely you will need to read this material several times before it starts to make sense. If it is still hazy after several readings, keep going. Eventually you will understand them, and wonder why it was such a big deal. We start by defining what is meant by the logarithm of a number to a particular base, and then look at several examples. Definition of a logarithm to a base a Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if ay x The number y is denoted by y log a x Another way to say the same thing is to say that y is the log of x to the base a, y log a x if when we raise a to the y th power we get x. Note that the logarithm to a base a is the inverse function of a x . We have chosen to define log functions directly rather than merely stating that they are particular inverse functions. The symbolism log a x is read as ”the log of x to the base a”, or ”the log to the base a of x”. Logarithms of various numbers to various bases are listed below. Be sure you understand each one of these. The logarithm of 10 to the base 10 equals 1: 10 1 10, log 10 10 1. The logarithm of 10 to the base 100 equals 0. 5: 100 1/2 10, log 100 10 1 . 2 2 The logarithm of 10 to the base 10 equals 2: 10 10, log 10 10 2. The logarithm of 100 to the base 10 equals 2: 10 2 100, log 10 100 2. The logarithm of 1000 to the base 10 equals 3: 10 3 1000, log 10 1000 3. The logarithm of 25 to the base 5 equals 2: 5 2 25, log 5 25 2. The logarithm of 64 to the base 2 equals 6: 2 6 64, log 2 64 6. The logarithm of 64 to the base 4 equals 3: 4 3 64, log 4 64 3. The logarithm of 64 to the base 8 equals 2: 8 2 64, log 8 64 2. © : Pre-Calculus © Question: Answer: Question: Answer: Example 1: Solution: : Pre-Calculus - Chapter 5D If 2. 3 4 x, what is a in log a x 4? 2. 3 If the logarithm of x to the base 3 is 4, then x must equal? 81. a y 3 4 81. If log 8 x 4, what is x? The statement log 8 x 4 has the same meaning as x 8 4 4096 . Example 2: Solution: If log a 9 2, what is a? log a 9 2 is equivalent to the statement a 2 9 or a 9 and since a 0 we have a 9 3. Example 3: You will later learn how to use your calculator to compute log 3 6. It turns out that log 3 6 ≈ 1. 6309. When a piece of technology is used to perform some calculation always ask yourself if the answer is reasonable. So, is 1. 6309 reasonable? Well 3 1 3 which is less than 6, so 1 should be less than the log of 6 to the base 3. The number 2 is larger than 1. 6309, so 3 2 which is 9 should be larger than 6 which it is. Thus, by these simple tests 1. 6309 seems reasonable. We now look at some plots of several log functions paying attention to their domains and ranges. Example 4: Plot log 10 x. y (10, 1) 10 x There are several things to note: 1. log 10 x is not graphed for x ≤ 0. That is, the domain of log 10 x is all positive real numbers. We’ll see why later. 2. The range of values of log 10 x is all real numbers. 3. log 10 1 0 4. The graph of log a x looks like the graph of log 10 x as long as a 1. © : Pre-Calculus © : Pre-Calculus - Chapter 5D In the next example we look at a plot of a log function where the base a is less than 1. Example 5: Plot log 1/2 x y 2 x ( 2, 1) This plot certainly looks different than the preceding one. However, there are certain similarities. 1. log 1/2 x is not graphed for x ≤ 0. That is, the domain of log 1/2 x is all positive real numbers. 2. The range of values of log 1/2 x is all real numbers. 3. log 1/2 1 0. 4. The graph of log a x looks like the graph of log 1/2 x as long as 0 a 1. To understand why the domain of any log function is only the positive real numbers, we look at the definition. That is, log a x y if and only if a y x. However, we’ve seen that numbers of the form a y are never less than or equal to zero. That is, a y x 0, and the x’s make up the domain of the log function. The fact that the range of log a x is all real numbers comes from the fact that in the second equation log a x y a x y the y’s can be any real number. © : Pre-Calculus © : Pre-Calculus - Chapter 5D Properties of Logarithms We list below some of the algebraic properties of logarithms. These properties should be memorized. 1. 2. 3. 4. 5. 6. 7. 8. The domain of log a x is all positive real numbers and its range is all real numbers. a log a x x log a a x x log a x log a y x y log a 1 0 log a xy log a x log a y log a x y y log a x log a xy log a x − log a y Proofs of the above properties: 1. This follows from the fact that the log a x is the inverse function of a x , and the fact that the domain of a x is all real numbers, while its range is all positive real numbers. 2. This follows directly from the definition. That is, log a x y where y is a number such that a y x. Thus, x a y a log a x . 3. This property also follows directly from the definition of log a x. That is, log a x y if and only if a y x. Thus, log a a x y if and only if a y a x . That is, x y log a a x . 4. If x y, then log a x log a y, for if not, then the fact that a x is a one-to-one function implies that x ≠ y. Conversely if log a x log a y, then we have x a log a x a log a y y . 5. Since a 0 1 no matter what a equals, we have log a 1 0 for any base a. 6. Let z log a xy, then we must have a z xy. However, we also have a log a xlog a y a log a x a log a y xy. Thus, a z a log a xlog a y from which we have log a xy z log a x log a y. 7. Let z log a x y . Then a z x y . Now compute a y log a x . a y log a x a log a x y x y x y . Thus, we have a z a y log a x . From this we deduce that log a x y z y log a x . 8. log a xy log a xy −1 log a x log a y −1 log a x − log a y Example 1: Let fx log 2 x − 1. What is the domain and range of fx? Plot this function. Solution: For any log function its argument must be greater than 0. Thus, domain of fx x : x − 1 0 x : x 1. The range of fx all real numbers. x=1 2 4 6 x 0 log2(x - 1) -5 -10 © : Pre-Calculus 8 10 12 14 © Example 2: Solution: : Pre-Calculus - Chapter 5D Simplify the expression 2 2 log 4 5 . 2 2 log 4 5 2 2 log 4 5 4 log 4 5 5. Example 3: Solution: Simplify log 3 16 log 3 5 − log 3 8. log 3 16 log 3 5 − log 3 8 log 3 16 5 − log 3 8 log 3 16 5 8 log 3 2 5 log 3 10 Example 4: Solution: Solve the equation 2 3 log 5 x 15. 2 3 log 5 x 15 3 log 5 x 13 log 5 x 13 3 x 5 13/3 ≈ 1068. 73 Example 5: Solve the equation 4 x−6 13. Solution: The easiest way to solve an equation in which the unknown is part of an exponent is to take the log of both sides of the equation. take the log 4 of both sides 4 x−6 13 x − 6 log 4 4 x−6 log 4 13 solve for x x 6 log 4 13 As we mentioned previously logarithms are the inverse functions of the exponential functions. On the next page we examine this relationship more closely for the two functions log 2 x and 2 x . Since log 2 x is the inverse function of 2 x we have log 2 x y if and only if x 2y . © : Pre-Calculus © : Pre-Calculus - Chapter 5D The following table demonstrates this relationship with specific numbers: 20 1 2 −1 1 2 23 8 2 −4 1 16 6 2 64 log 2 1 0 log 2 1 −1 2 log 2 8 3 log 2 1 −4 16 log 2 64 6 There is nothing special about base 2 in this relationship. For every base a it is true that log a x y if and only if x ay There is another way to write these relationships, and it is log a a x x a log a x x Question: Answer: If a 3 4. 56, what is log a 4. 56? log a 4. 56 log a a 3 3 The graph below contains a plot of 2 x and log 2 x. (2,4) y=2 x (1,2) (4,2) (0,1) (2,1) (1,0) y=x y = log 2 x Notice that each plot is the reflection of the other about the line y x. Question: Answer: © If log 2 15 y, what does 2 y equal ? 15. If log 2 15 y, then 2 y 2 log 2 15 15 . : Pre-Calculus © : Pre-Calculus - Chapter 5D Natural Logarithm The natural log function is that log function which has base e. This function is so commonly used that instead of writing log e x we write ln x. Hence, ln represents log e . To repeat ourselves ln x is the inverse function of e x , and the usual relationships between a function and its inverse hold. lne x x e ln x x . Example 1: Solution: Compute the natural log of 5, 0. 45, 17, and 1. ln 5 ≈ 1. 609 44 ln 0. 45 ≈ − 0. 798 508 ln 17 ≈ 2. 833 21 ln 1 0 Example 2: Plot e x and ln x on the same graph. y x Question: Answer: In the above plot which of the two curves is the graph of ln x? ln x is the graph drawn in red. Question: Answer: In the above plot what are the coordinates of the point where the red curve crosses the x-axis ? 1, 0 Question: Answer: In the above plot what are the coordinates of the point where the blue curve crosses the y-axis ? 0, 1 It is possible to write every log function in terms of the natural log function. We show how to do so here. Suppose y log a x. Then x a y . The next step is to express a in terms of e. We have a e ln a . Thus, x ay e ln a y e y ln a . Taking the natural log of both sides of this equation, we derive ln x y ln a y ln x or ln a log a x ln x . ln a © : Pre-Calculus © : Pre-Calculus - Chapter 5D There are two formulas that should be remembered, and we list them once more. a x e x ln a log a x ln x ln a This formula will be useful in many of the exercises at the end of this chapter. Be sure you understand its derivation. Example 3: Solution: Write log 8 15 using the natural logarithm. log 8 15 ln 15 ln 8 2. 708 05 ≈ 2. 079 44 ≈ 1. 302 3 Example 4: In an earlier chapter we said that a function has exponential growth if it has the form fx a kx . Write this function in terms of the natural exponential function. Solution: fx a kx e ln a kx e k ln ax . This last example shows us that any function which has exponential growth can be written in terms of the natural base e ≈ 2. 718 28. Example 5: Solution: Solve the equation e 5x−6 18. The way to solve this equation is to take the natural log of both sides. e 5x−6 18 5x − 6 ln 18 5x ln 18 6 x ln 18 6 5 x ≈ 1. 778 07 Example 6: and k. Solution: Suppose that fx ae kx for some value of k and a. Suppose that f1 2 and f3 1. Find a The values of fx when x 1 and x 3 lead to the following equations. 2 f1 ae k 1 f3 ae 3k We have a system of two equations in two unknowns. One way to solve a system which involves exponential functions is to first take the natural log of both sides. Doing so we get ln 2 lnae k ln a lne k ln a k ln 1 lnae 3k ln a lne 3k ln a 3k Since ln 1 0, the second equation implies that ln a −3k. Substituting this into the first equation we have ln 2 −3k k −2k k ln 2 . −2 3 ln 2 Hence, ln a −3k −3 ln 2. Thus, a 2 3/2 . Substituting these values into the formula for fx, we 2 −2 have © : Pre-Calculus © : Pre-Calculus - Chapter 5D ln 2 x fx 2 3/2 e −2 2 3/2 e ln 2 −x/2 2 3/2 2 −x/2 3−x 2 2 © : Pre-Calculus © : Pre-Calculus - Chapter 5D Exercises for Chapter 5D - Logarithmic Functions 1. Who invented logarithms? 2. What is the domain of log 2 x 1? 3. What are the domain and range of log 3 2x − 1? 4. What are the domain and range of log 5 1 x − 1 ? 5. If x log a 5, what does a x equal ? 6. Does log 4 2 equal log 2 4 ? 7. Compute the following logarithms: log 10 15, log 8 15, log 6 15, and log 4 15. Do you see a relationship between the numbers ? 8. Compute the following logarithms: log 16 10, log 4 10, and log 2 10. Do you see a relationship between these numbers ? 9. Solve log 5 25 x 4. 10. Solve the equation 5 2x−1 6. 5. 11. Which number is larger log 9 3 or log 3 9 ? 12. If x log 4 23, what does 2 x equal ? 13. Express the equation log 15 x − 2 5 in exponential form. 14. Solve 4 x2 15. 15. If log 4 6 log 2 x, what does x equal? 16. If x 0, what does log x x equal ? 17. Express the equation 15 x 2 −3 9 in logarithmic form, then solve for x. 18. Which number is larger log 10 100 or log 9 100? 19. Which number is larger log 10 1 of log 9 1 ? 2 2 20. 5 is larger than 4, thus, for x 1 we expect log 4 x to be larger than log 5 x. It takes more 4’s to equal x than it does 5’s. Plot these two functions for x 1 and graphically verify this © : Pre-Calculus © : Pre-Calculus - Chapter 5D conjecture. 21. Solve log 4 x − log 4 x − 1 5. 22. Simplify log 10 x 2 log 10 x 3 − log 10 5x. 23. Simplify log 3 2x − 7 log 3 x 5. 24. Simplify 1 log 3 16 − log 3 24. 2 25. Simplify log a x − log a 1x . 26. Simplify log a x 3 − log a 3x log a 1x . 27. Solve the equation 2 log 5 x − log 5 x 1. 3. 28. Solve the equation log 3 2x log 3 x 4 − 5 0. 29. If log 4 x log 4 43, what must x equal ? 30. Write log 9 15 in terms of the natural logarithm. 31. Compute the numbers: ln 64, ln 32, ln 16, and ln 8. 32. Solve the expression x ln 32 ln 2. 33. What is the domain of lnx 4? 34. Write log a 2 x in terms of log a . 35. If log 10 x 3. 5, then log 15 x equals? 36. Which is the larger number log 5 x or ln x ? 37. Find a relationship between log a x and log a 2 x. 38. Find the domain of y e xa ln2x − b 39. Solve for x: x lna b lna 40. Given log b 2 a, log b 3 c, and log b 5 f. Find log b 1800. © : Pre-Calculus © : Pre-Calculus - Chapter 5D Answers to Exercises for Chapter 5D - Logarithmic Functions 1. 2. John Napier, a Scotsman. In the function log 2 x 1 the expression x 1 must be positive, since the domain log 2 x is all positive real numbers. Thus, we must have x1 0 x −1 . 3. 4. If x is in the domain of log 3 2x − 1, then we must have 2x − 1 0 2x 1 x 1 2 1 So the domain of log 3 2x − 1 is x . Morever as x varies over the interval 1/2, , 2 2x − 1 varies over the interval 0, . This means that the range of log 3 2x − 1 is the same as the range of log 3 x, i.e., all real numbers. There are two problems in determining the domain of log 5 1 x − 1 . One we need to ensure that 1 x−1 0 and that x − 1 ≥ 0 so that we can take its square root. Since square roots are always non-negative adding 1 to x − 1 will certainly make 1 x − 1 positive. Thus, the domain of log 5 1 x − 1 is 5. 6. 7. x ≥ 1. To determine the range of log 5 1 x − 1 we observer that as x varies over the interval 1, , the expression 1 x − 1 varies over the interval 1, , and thus the values of log 5 1 x − 1 will vary over the interval 0, . 5 log 2 4 2 No. log 4 2 12 log 10 15 ≈ 1. 176 09 log 8 15 ≈ 1. 302 3 log 6 15 ≈ 1. 511 39 log 4 15 ≈ 1. 953 45 As far as a relationship is concerned the smaller the base the larger the value of the logarithm. 8. log 16 10 ≈ . 830 482 log 4 10 ≈ 1. 660 96 log 2 10 ≈ 3. 321 93 Notice that as we take the square root of the base the logarithm doubles. © : Pre-Calculus © : Pre-Calculus - Chapter 5D 9. log 5 25 x 4 2x 4 x2 10. 5 2x−1 6. 3 2x − 1 log 5 6. 3 2x 1 log 5 6. 3 1 log 5 6. 3 x 2 ≈ 1. 071 8 log 9 3 1 log 3 9 2 2 log 23 4 1/2 4 4 log 4 23 1/2 23 1/2 ≈ 4. 795 83 11. log 3 9 is larger. 12. 2 x 2 log 4 23 13. x − 2 15 5 14. 4 x2 15 implies x 2 log 4 15 x log 4 15 − 2 x ≈ 1. 953 45 − 2 x ≈ −4. 655 47 10 −2 15. log 4 6 log 2 x implies x 2 log 2 x 2 log 4 6 4 1/2 log 4 6 4 log 4 6 1/2 6 1/2 . 16. 1 2 17. To express 15 x −3 9 as a logarithmic equation take the log to base 15 of both sides. 2 15 x −3 9 x 2 − 3 log 15 9 ≈ 0 . 811 368 This leads to the equation x 2 3. 811368 x 3. 811368 ≈ 1. 952 27 18. log 9 100 is larger, for the reason that it will take a higher power of 9 to equal 100 than for 10. In fact, these numbers are approximately log 10 100 2. 0 log 9 100 ≈ 2. 095 9 19. log 10 1 2 © : Pre-Calculus © : Pre-Calculus - Chapter 5D 20. y log 4( 25 ) = 2.3215 log 5( 25 ) = 2 25 21. log 4 x − log 4 x − 1 5 implies log 4 x x−1 x x 4 5 This leads to the equation x−1 x x − 14 5 5 x x 45 − 45 x1 − 4 5 −4 5 −4 5 1 − 45 ≈ 1. 000 98 x 22. log 10 x 2 log 10 x 3 − log 10 5x 2 log 10 x 3 log 10 x − log 10 x − log 10 5 4 log 10 x − log 10 5 log 10 x 4 − log 10 5 4 log 10 x . 5 23. log 3 2x − 7 log 3 x 5 log 3 2x − log 3 x 5 7 2x log 3 x 5 7 24. 1 log 16 − log 24 log 16 1/2 − log 24 3 3 3 3 2 log 3 4 24 log 3 1 6 − log 3 6 25. log a x − log a 1x log a x − log a x −1 log a x log a x 2 log a x log a x 2 26. log a x 3 − log a 3x log a 1x 3 log a x − log a 3 log a x − log a x log a x − log a 3 log a x 3 © : Pre-Calculus © : Pre-Calculus - Chapter 5D 26. log a x 3 − log a 3x log a 1x 3 log a x − log a 3 log a x − log a x log a x − log a 3 log a x 3 27. 2 log 5 x − log 5 x 1. 3 2 log 5 x − 1 log 5 x 1. 3 2 3 log x 1. 3 5 2 log 5 x 2. 6 3 2.6/3 x5 ≈ 4. 034 35 28. log 3 2x log 3 x 4 − 5 0 log 3 2 log 3 x 4 log 3 x 5 5 log 3 x 5 − log 3 2 5 − log 3 2 log 3 x 5 log 3 2 1− 5 Thus, x3 1− log 3 2 5 3 3 −log 3 2/5 33 log 3 2 −1/5 31/5 2 ≈ 2. 611 65 29. 43 30. log 9 15 ln 15 ln 9 31. ln 64 ≈ 4. 158 88 ln 32 ≈ 3. 465 74 ln 16 ≈ 2. 772 59 ln 8 ≈ 2. 079 44 © : Pre-Calculus © : Pre-Calculus - Chapter 5D 32. x ln 32 ln 2 x ln 2 ln 32 ln 25 ln2 ln 2 5 ln 2 1 5 33. If x is in the domain of lnx 4, then we must have x4 0 x −4 . 34. log a 2 x ln x2 ln a ln x 2 ln a 1 log a x 2 35. log 15 x ln x ln 15 ln 10log 10 x ln 15 ln 103. 5 ln 15 8. 059 07 ≈ 2. 708 05 ≈ 2. 975 97 36. ln x is log e x. If x 1, since e is less than 5, ln x will be larger than log 5 x. If 0 x 1, ln x will be smaller than log 5 x. 37. log a 2 x ln x2 ln a ln x 2 ln a 1 ln x 2 ln a 1 log a x . 2 38. Here we must check two things. We must make sure we are only taking the log of positive numbers and we must make sure we are not dividing by zero: © : Pre-Calculus © : Pre-Calculus - Chapter 5D 2x − b 0 2x b x b 2 and ln2x − b ̸ 0 2x − b ̸ 1 2x ̸ 1 b x ̸ 1 b 2 Thus, the domain is b, 1b 2 2 1 b , 2 39. x lna b lna xb lna lna lna x b lna x 1 b ̸ 0 b 40. We want to write 1800 as the product of powers of 2, 3, and 5. One way to do this is as follows: 1800 2598 5 2 3 2 2 3 Thus, log b 1800 log b 5 2 3 2 2 3 log b 5 2 log b 3 2 log b 2 3 2 log b 5 2 log b 3 3 log b 2 2f 2c 3a © : Pre-Calculus