Download 7.1- Triangle Application Theorems

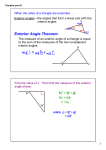
Warm Up
Answer
7.1- Triangle Application
Theorems
Objective- apply theorems about
interior angles, the exterior angles
and the midlines of triangles
T50- the sum of the measures of the
angles of a triangle is 180
Given: triangle ABC
Prove m<A+ m<B
+m<C = 180*
Proof
According to the Parallel Postulate , these exists
exactly one line through point A parallel to
BC so the figure at the right can be
drawn…
<1 + <2 + <3 = 180 (straight
line)
<1= <C alt. int. <s
<3=<B alt. int. <s
So m<A +m<B+ m<C= 180
Exterior angles of a polygon
Definition- an exterior angle of a polygon is an angle
that is adjacent to and supplementary to an interior
angle of the polygon
More Theorems!
(please applaud now!)
T51- triangles only: the measure of an exterior angle
of a triangle is equal to the sum of the measures of
the remote interior angles
T52- A segment joining the midpoints of two sides
of a triangle is parallel to the third side and its
length is 1/2 the length of the third side.
Proof of Theorem 51
m<BCA +m<1 = 180
m<BCA + m <B + m<A = 180
m <BCA + m <1 = m <BCA + m <B +m <A
m <1 = m <B + m <A
Proof for Theorem 52
P