* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Geometry Worksheet 5
History of geometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Multilateration wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
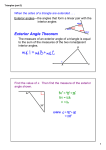
Geometry Worksheet 5.2 Inequalities and Triangles Name _______________________ Per ___ Date _________________ 1. Exterior Angle Inequality Theorem: The exterior angle of a triangle is _________ Than its two ____________ ___________ angles. 2. Angle-Side Relationships: The longest side of a triangle is ____________ from the ________________ in that triangle. Determine which angle has the greatest measure: 3. 4. 4, 3, 1 4, 3, 1 1 3 2 5. 4, 3, 2 3 2 1 4 2 4 1 3 4 6. 7. 2, 5, 7 5 3 2 1 4 2, 4, 6 5 3 2 1 4 7 6 7 6 8. 7, 3, 1 5 3 2 1 4 7 6 9. Name all angles that measure less than m 1 7 10. Name all angles that measure greater than m 6 6 5 4 8 2 3 11. Name all angles that measure less than m 7 1 Determine if the angles are greater than (>), less than (<), or equal (=) to each other. 12. m ABD _____ m BAD 13. m ADB _____ m BAD 14. m BCD _____ m CDB 15. m WXY _____ m XYW 16. m XZY _____ m XYZ 17. m WYX _____ m XWY Determine if the sides are greater than (>), less than (<), or equal (=) to each other. 18. LM _____ LP 19. MP _____ MN 20. NM _____ NP 21. AE _____ EB 22. CE _____ CD 23. BC _____ EC 24. All angles in a triangle add up to ____________________. Use the fact from problem number 24 to solve the problems below. Find the value of n and list the sides of PQR in order from longest to shortest. 25. n = _______________ 26. n = _______________ 27. n = _______________ m R 10n 2 m R 16n 2 m R 68 2n _____, ______, ______ _____, ______, ______ _____, ______, ______ m P 9n 29, m Q 93 5n, m P 12n 9, m Q 62 3n, m P 9n 4, m Q 4n 16, 28. Find x if AD is a median of 29. Finish the proof: ABC