* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 7.1- Triangle Application Theorems
Multilateration wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Four color theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
History of trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Integer triangle wikipedia , lookup
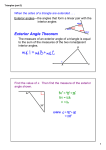
Warm Up Answer 7.1- Triangle Application Theorems Objective- apply theorems about interior angles, the exterior angles and the midlines of triangles T50- the sum of the measures of the angles of a triangle is 180 Given: triangle ABC Prove m<A+ m<B +m<C = 180* Proof According to the Parallel Postulate , these exists exactly one line through point A parallel to BC so the figure at the right can be drawn… <1 + <2 + <3 = 180 (straight line) <1= <C alt. int. <s <3=<B alt. int. <s So m<A +m<B+ m<C= 180 Exterior angles of a polygon Definition- an exterior angle of a polygon is an angle that is adjacent to and supplementary to an interior angle of the polygon More Theorems! (please applaud now!) T51- triangles only: the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles T52- A segment joining the midpoints of two sides of a triangle is parallel to the third side and its length is 1/2 the length of the third side. Proof of Theorem 51 m<BCA +m<1 = 180 m<BCA + m <B + m<A = 180 m <BCA + m <1 = m <BCA + m <B +m <A m <1 = m <B + m <A Proof for Theorem 52 P