* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download l - Evergreen
Neutron magnetic moment wikipedia , lookup
Electromagnetism wikipedia , lookup
Electromagnetic field wikipedia , lookup
Ising model wikipedia , lookup
Lorentz force wikipedia , lookup
Skin effect wikipedia , lookup
Electromagnet wikipedia , lookup
Electron paramagnetic resonance wikipedia , lookup
History of geomagnetism wikipedia , lookup
Multiferroics wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Giant magnetoresistance wikipedia , lookup
Ferromagnetism wikipedia , lookup
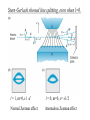
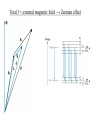
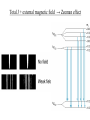
Start EM Ch.5: Magnetostatics finish Modern Physics Ch.7: J=L+S Methods of Math. Physics, Thus. 24 Feb. 2011, E.J. Zita Magnetostatics: • Lorentz Force and Biot-Savart Law • Divergence and Curl of B; Ampere’s Law Modern Physics • Spin, Energy levels, Zeeman effect • Fine structure, Bohr magneton, J=L+S Ex.5.2: Cycloid motion: B=Bx, E=Ez, find particle motion if it starts from rest at the origin. 1. Draw. 2. Qualitative analysis. 3. Quantitative analysis. xˆ yˆ v B 0 dy dt B 0 zˆ dz dt 0 Ex.5.4: (a) A current I is uniformly distributed over a wire of circular cross section with radius a. Find J. Ex.5 (b) Suppose the current density in the wire is proportional to the distance from the axis: J=ks (for some constant k). Find the total current in the wire. Finding field B from current I • Biot Savart law in general (5.32, p.215) • Ampere’s law, when symmetry permits (p.221) Draw Ampere’s law: Apply Stokes’ Thm. to Magnetostatics B d a surface B dl 0 I boundary dI current density J , so I J da da surface B d a 0 surface surface B 0 J J da Using Ampere’s law 1. Draw, 2. Qualitative analysis, 3. Quantitative Find B for an infinite uniform surface current K=Kx over the xy plane. (I=dK/dlength) Using Ampere’s law 1.Draw, 2. Qualitative analysis, 3. Quantitative Find B for a solenoid with n closely wound turns per unit length on a cylinder of radius R and carrying a steady current I. We’ll finish Ch.5 next week. Choose some HW problems… Continuing Modern Physics Ch.7: H atom in Wave mechanics • Spin, Energy levels • Zeeman effect • Fine structure • Bohr magneton • J=L+S H-atom wavefunctions ↔ electron probability distributions: l = angular momentum wavenumber Discussion: compare Bohr model to Schrödinger model for H atom. ml denotes possible orientations of L and Lz (l=2) Wave-mechanics L ≠ Bohr’s n Stern-Gerlach showed line splitting, even when l=0. l = 1, m=0,±1 ✓ l = 0, m=0, s= ±1/2 Normal Zeeman effect Anomalous Zeeman effect Magnetic moments shift energies in B fields Spin S and orbit L couple to total angular momentum J = L+ S Spin-orbit coupling: spin of e- in orbital magnetic field of p Fine-structure splitting (e.g. 21-cm line) (Interaction of nuclear spin with electron spin (in an atom) → Hyper-fine splitting) Total J + external magnetic field → Zeeman effect Total J + external magnetic field → Zeeman effect Total J + external magnetic field → Zeeman effect History of atomic models: • Thomson discovered electron, invented plum-pudding model • Rutherford observed nuclear scattering, invented orbital atom • Bohr quantized angular momentum, improved H atom model. • Bohr model explained observed H spectra, derived En = E/n2 and phenomenological Rydberg constant • Quantum numbers n, l, ml (Zeeman effect) • Solution to Schrödinger equation shows that En = E/l(l+1) • Pauli proposed spin (ms= ±1/2), and Dirac derived it • Fine-structure splitting reveals spin quantum number