Download Particle Filters (Part 2)

Today
• Introduction to MCMC
• Particle filters and MCMC
• A simple example of particle filters: ellipse
tracking
Introduction to MCMC
• Sampling technique
– Non-standard distributions (hard to sample)
– High dimensional spaces
• Origins in statistical physics in 1940s
• Gained popularity in statistics around late
1980s
• Markov Chain Monte Carlo
Markov chains*
Series of samples
such that
x (i )    {x1 , x2 ,, xs }
p( x (i ) | x (i 1) ,, x (1) )  T ( x (i ) | x (i 1) )
• Homogeneous: T is time-invariant
– Represented using a transition matrix
1
0
0
T   0 0.1 0.9
0.6 0.4 0 
* C. Andrieu et al., “An Introduction to MCMC for Machine Learning“, Mach. Learn., 2003
Markov chains
• Evolution of marginal distribution
Bayes’ theorem
pi ( x (i ) ) 
( i 1)
(i )
( i 1)
p
(
x
)
T
(
x
|
x
)
 (i1)
x ( i 1)
• Stationary distribution
pi  p(i 1)  p
• Markov chain T has a stationary distribution
– Irreducible
– Aperiodic
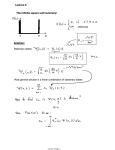
Markov chains
• Detailed balance
– Sufficient condition for stationarity of p
p( x (i ) )T ( x (i 1) | x (i ) )  p( x (i 1) )T ( x (i ) | x (i 1) )
• Mass transfer
p( x (i ) ) 
Probability
mass
( i 1)
(i )
( i 1)
p
(
x
)
T
(
x
|
x
)

x ( i 1)
Probability
mass
Proportion of
mass transfer
T ( x (i ) | x (i 1) )
x(i)
Pair-wise balance of
mass transfer
p( x (i 1) )
x(i-1)
T ( x (i 1) | x (i ) )
p( x (i ) )
Metropolis-Hastings
• Target distribution: p(x)
• Set up a Markov chain with stationary p(x)
x (i ) 
 x (i 1)
Propose
x
( i 1)
x* ~ q( x* | x ( i ) )
x
*
x ( i 1)  x ( i )
with probability
(Easy to sample from q)
 p( x* )q( x ( i ) | x* ) 

A( x , x )  min 1,
(i )
*
(i ) 
 p( x )q( x | x ) 
(i )
*
otherwise
• Resulting chain has the desired stationary
– Detailed balance
Metropolis-Hastings
• Initial burn-in period
– Drop first few samples
• Successive samples are correlated
– Retain 1 out of every M samples
• Acceptance rate
– Proposal distribution q is critical
Monte-Carlo simulations*
• Using N MCMC samples
• Target density estimation
• Expectation
• MAP estimation
– p is a posterior
* C. Andrieu et al., “An Introduction to MCMC for Machine Learning“, Mach. Learn., 2003
Tracking interacting targets*
• Using partilce filters to track multiple interacting
targets (ants)
* Khan et al., “MCMC-Based Particle Filtering for Tracking a Variable Number of
Interacting Targets”, PAMI, 2005.
Particle filter and MCMC
• Joint MRF Particle filter
– Importance sampling in high dimensional
spaces
– Weights of most particles go to zero
– MCMC is used to sample particles directly
from the posterior distribution P( X t | Z t )
MCMC Joint MRF Particle filter
• True samples (no weights) at each step
{ X tr1}rN1 ~ P( X t 1 | Z t 1 )
• Stationary distribution for MCMC
n
P( X t Z )  cP( Z t X t )   ( X it , X jt ) P( X it X ir(t 1) )
t
i , jE
r
i 1
• Proposal density for Metropolis Hastings (MH)
– Select a target randomly
– Sample from the single target state proposal density
MCMC Joint MRF Particle filter
• MCMC-MH iterations are run every time step
to obtain particles
• “One target at a time” proposal has
advantages:
– Acceptance probability is simplified
– One likelihood evaluation for every MH iteration
– Computationally efficient
• Requires fewer samples compared to SIR
Particle filter for pupil (ellipse)
tracking
• Pupil center is a feature for eye-gaze
estimation
• Track pupil boundary ellipse
Outliers
Pupil boundary edge points
Ellipse overlaid on the eye image
Tracking
• Brute force: Detect ellipse every video frame
– RANSAC: Computationally intensive
• Better: Detect + Track
– Ellipse usually does not change too much between
adjacent frames
• Principle
–
–
–
–
Detect ellipse in a frame
Predict ellipse in next frame
Refine prediction using data available from next frame
If track lost, re-detect and continue
Particle filter?
• State: Ellipse parameters
• Measurements: Edge points
• Particle filter
– Non-linear dynamics
– Non-linear measurements
• Edge points are the measured data
Motion model
• Simple drift with rotation
State
X  ( x0 , y0 , a, b, )
(x0 , y0 )
θ
Could include velocity,
acceleration etc.
a
b
P( X t | X t 1 )   ( x0(t 1) ,  x20 ) ( y0(t 1) , y20 ) (at 1 ,  a2 ) (bt 1 , b2 ) (t 1 ,  2 )
Gaussian
Likelihood
• Exponential along normal at each point
z6 d
6
z1
z5
d5
d1
z2
d2
z3
z4 d
4
d3
P(Z | X )   P( zi | X )  exp( 
i
1
d)


i
i
• di: Approximated using focal bisector distance
Focal bisector distance* (FBD)
Foci
FBD
Focal bisector
• Reflection property: PF’ is a reflection of PF
• Favorable properties
– Approximation to spatial distance to ellipse boundary along
normal
– No dependence on ellipse size
* P. L. Rosin, “Analyzing error of fit functions for ellipses”, BMVC 1996.
Implementation details
• Sequential importance re-sampling*
P( X t Z )  cP( Z t X t )  tr1 P( X t X tr1 )
t
r
Weights:
Proposal distribution:
Likelihood
Mixture of Gaussians
• Number of particles:100
• Expected state is the tracked ellipse
• Possible to compute MAP estimate?
* Khan et al., “MCMC-Based Particle Filtering for Tracking a Variable Number of
Interacting Targets”, PAMI, 2005.
Initial results
Frame 1: Detect
Frame 2: Track
Frame 4: Detect
Frame 5: Track
Frame 3: Track
Frame 6: Track
Future?
• Incorporate velocity, acceleration into the
motion model
• Use a domain specific motion model
– Smooth pursuit
– Saccades
– Combination of them?
• Data association* to reduce outlier
confound
* Forsyth and Ponce, “Computer Vision: A Modern Approach”, Chapter 17.
Thank you!