Download Section 6.2 Introduction to Groups

1
Section 6.2
Introduction to Groups
Section 6.2 Introduction to the Algebraic Group
Purpose of Section:
Section To introduce the concept of a mathematical structure
called an algebraic group. To illustrate group concepts, we introduce cyclic
and dihedral groups.
Introduction
The theory of groups is an area of mathematics which is concerned with
underlying relationships of things, and arguably the most powerful tool ever
created for illuminating structure, both mathematical and physical. The word
group was first used by the French genius Evariste Galois in 1830, who wrote
his seminal paper on the unsolvability of the 5th order polynomial equation, the
night before he was killed in a stupid duel at the age of 20. Other early
contributors to the development of group theory were Joseph Louis Lagrange,
(1736-1813), Niels Abel (1802-1829), Augustin-Louis Cauchy (1789-1857),
Arthur Cayley (1821-1895, Camille Jordan (1838-1923), Ludwig Sylow (18321918) and Marius Sophus Lie (1842-1899). Now, merely more than a century
later, group theory has resulted in an amazing unification of areas of
mathematics, including algebra and geometry, long thought to be separate and
unrelated. It is often said that whenever groups make an appearance in a
subject, simplicity is created from chaos. Group theory has played (and is
playing) a crucial role for both chemists and physicists to penetrate the deep
underlying relationships in our amazing world.
Binary Operation and Groups
Groups
A binary operation on a set A is a rule, which assigns to each pair of
elements of A a unique element of A . Thus, a binary operation is simply a
function f : A × A → A . Two common binary operations familiar to the reader
are +, i which assign the sum a + b ∈ and product a i b∈ to a pair
( a, b ) ∈ × of real numbers. We now give a formal definition of a group.
2
Section 6.2
Introduction to Groups
Definition:
Definition An algebraic group
group G (or simply group)
group is a set of elements with a
binary operation,
operation say “ ∗ ”, satisfying the closure
closure property
a, b ∈ G ⇒ a * b ∈ G
as well as the following properties:
▪
Associative: ∗ is associative,
associative that is, for every a, b, c ∈ G , we
have
( a ∗ b ) ∗ c = a ∗ (b ∗ c ) .
▪ Identity: G has a unique identity1 e .
have a * e = e * a = a
That is, for any element a ∈ G we
▪ Inverse: Every element a ∈ G has a unique inverse2 . That is, for a ∈ G
there exists an element a −1 ∈ G that satisfies a * a −1 = a −1 * a = e .
We often denote a group G with operation "∗ " by {G, ∗} .
Often it happens that a ∗ b = b ∗ a for all a, b ∈ G . When this happens the group
is called a commutative (or Abelian)
We often denote the group
Abelian group.
operation a ∗ b as ab , or maybe something more suggestive like ⊕ if the
group operation is addition or closely resembles addition. A group is called
finite if it contains a finite number of elements and the number of elements in
the group is called the order of the group. If the order of a group G is n , we
denote this by writing G = n
If the group is not of finite order we say it is
of infinite order.
order
In Plain English
▪ Associative: The associative property tells us when we combine three
elements a, b, c ∈ G (keeping them in the same order), the result is unchanged
regardless of which two elements are combined first. There are examples of
algebraic groups where the operation is not associative, the cross product of
vectors in vector analysis is an example of a non-associative operation, as
well as the difference between two numbers3, but by far the majority of binary
operations in mathematics are associative.
1
It is not necessary to state that the identity is unique since it can be proven there is only one identity. In a
more lengthy treatment of groups, we would define the existence of an identity and then prove it is unique,
but here we assume uniqueness to shorten the discussion.
2
Again, it can be proven that the inverse is unique so it is not really necessary to assume uniqueness of an
inverse in the definition.
3
( a − b) − c ≠ a − (b − c) .
3
Section 6.2
Introduction to Groups
▪ Identity: The identity element of a group depends on the binary relation ∗
and is the unique element e ∈ G that leaves every element a ∈ G unchanged
when combined with e . In the group of the integers with the binary
operation + (addition), the identity is 0 since a + 0 = 0 + a = a for every
integer a . If the binary operation is × (multiplication), then the identity e is 1
since a ×1 = 1× a = a for all a in the group.
▪ Inverse: The inverse a −1 of an element a depends (of course) on the
element a , but also on the identity e and is an element such that when
combined with a yields the identity; that is aa −1 = a −1a = e . For example, the
inverse of an integer a with group operation addition + is its negative − a since
a + ( −a ) = ( −a ) + a = 0 .
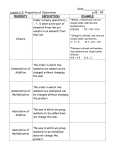
Operation
Table 1: Properties of Binary Operations
Associative
Commutative
Identity
Inverse
∪ on P ( A)
Yes
Yes
Yes
No
∩ on P ( A)
Yes
Yes
Yes
Yes
gcd on + on − on × on min on Yes
Yes
No
Yes
Yes
Yes
Yes
No
Yes
Yes
No
Yes
No
Yes
No
No
Yes
No
Yes
No
Example 1: Group Test
Which of the following define a group on the set of integers?
a)
b)
c)
{, +} : Integers with the operation of addition.
{, (m + n) / 2} : Integers with operation of averaging two integers.
{, −} Integers with operation of taking the difference of two integers.
Solution
a)
{, +} : We leave it to the reader to show {, +} is a group.
b)
{, (m + n) / 2} :
See Problem 5.
Taking the average of two integers, say 2 and 3, is not an
integer, hence the averaging operation is not closed in . Hence with the
averaging operation is not a group. There is no need to check the other
properties required of a group.
4
Section 6.2
c)
{, −}
Introduction to Groups
The integers with the difference operation is not a group since
subtraction is not associative, i.e. m − ( n − p ) ≠ ( m − n ) − p . However, it does
have an identity, 0 since 0 − m = −m − 0 = − m . Also, every integer has an
inverse, itself, i.e. m − m = 0, − m − ( − m ) = 0 . Nevertheless, failure of the
associative property says it is not a group.
Abstraction Abstraction reveals connections between different areas of mathematics
since the process of abstraction allows one to see essential ideas and see the “forest and
not just the trees.” This broad viewpoint can result in making new discoveries in one
area of mathematics as a result of knowledge in other areas. A disadvantage might be
that highly abstract mathematics is more difficult to master and tends to isolate
mathematics from the outside world.
Cayley Table
The binary operation of a group can be illustrated by means of a Cayley4 table as
drawn in Table 2, which shows the products gi g j of elements gi and g j of a group. It is
much like the addition or multiplication tables the reader studied as a child, except a
Cayley table can record any binary operation. A Cayley table is an example of a latin
square, meaning that every element of the group occurs once and exactly once in every
row and column. We examine the Cayley table to learn about the inner workings of a
group.
∗
g1 = e
g2
g3
gj
g1 = e
e
g1
g2
gj
g2
g2
g 22
g 2 g3
g2 g j
gi
g i g1
gi g 2
gi g 3
gi g j
Cayley Table for a Group
Figure 2
Example 2
Below we illustrate the only groups of order 2 and 3. Show they are both
commutative. Find the inverse of each element in the group. Show that each
group is associative. Convince yourself that the only groups of these orders
are the ones given. Keep in mind every row and column of the multiplication
4
Arthur Cayley (1821-1895) was an English mathematician
5
Section 6.2
Introduction to Groups
table includes every element of the group exactly once. We leave this fun for
the reader.
Order 2
*
e
a
e
e
a
a
a
e
Order 3
*
e
a
b
e
e
a
b
a
a
b
e
b
b
e
a
Example 3: The set G = {a, b, c, d } and binary operation * define a group
illustrated by the Cayley table
a) Is there an identity element? If so, find it.
b) Find the inverse of each element.
c) Is the binary operation commutative?
d) Is a * ( b * c ) = ( a * b ) * c
Solution
a) The identity is a since ab = ba = b, ac = ca = c, ad = da = d .
b) a −1 = a, b −1 = d , c −1 = c, d −1 = b
c) yes, the multiplication table is symmetric around the main diagonal
d) yes, a * ( b * c ) = a * d = d and ( a * b ) * c = b * c = d . In general, there is
no quick way to verify the associative property like there is the commutative
property.
You have to check ALL possible arrangements to verify
associativity.
On the other hand, if one instance where associativity fails,
then the binary operation * is not associative.
6
Section 6.2
Introduction to Groups
Example 4: Klein 4-Group
Show that the set G = {e, a, b, c} described by the multiplication table in
Figure 1 forms a group. This group is called the Klein5 4-group,
group which is the
symmetry group of a (non square) rectangle6 studied in Section 6.1. There
are exactly two distinct groups of order four, the Klein 4-group and the cyclic
group 4 which we will study shortly.
∗
e
a
b
c
e
e
a
b
c
a
a
e
c
b
b
b
c
e
a
c
c
b
a
e
Multiplication Table for the Klein four-group
Figure 1
Proof: First observe all products of elements of G belong to G since the
table consists only of elements of G . The hardest requirement to check is
associativity, which requires we check ( r ∗ s ) ∗ t = r ∗ ( s ∗ t ) , where r , s can be
any of the elements e, a, b, c , which means we have 43 = 48 equations to check
since each or the r , s, t in the associative formula can take on one of four
values e, a, b, c . The computations can be simplified by observing the group is
commutative (i.e. r ∗ s = s ∗ r for all r , s ∈ G ), which implies ( r ∗ r ) ∗ r = r ∗ ( r ∗ r )
so we have associativity when r = s = t . Other shortcuts tricks can be used
(as well as computer algebra systems) to shorten the list of elements you
must check. In this example, we observe that the group operation ∗ is simply
the composition of functions and we can resort to the fact that composition of
functions is associative.
Finding the group identity e is easy since multiplying any member of the
group by e , either on the left of right, does not change the member. You can
see that the first row and column of the table are the same as the group
elements themselves.
5
Felix Klein (1849-1925) was a German geometer and one of the major mathematicians of the 19th
century.
6
Try interpreting the elements e, a of the Klein group are 0 and 180 degree rotations of a rectangle, and
c, d the horizontal and vertical flips of the rectangle..
7
Section 6.2
Introduction to Groups
Finally, to find the inverse r −1 of an element r simply follow along the
row labeled " r " until you get to the group identity e , then the inverse r −1 is
the column label above e . You could also do the same thing by going down
the column labeled " r " until reaching e , then the row label at the left of e is
r −1 . In the Klein four-group each element 1, a, b, c is its own inverse since the
identity e lies along the diagonal of the “multiplication” table.
Familiar Groups
You are familiar with more groups that you probably realize. Table 2
shows just a few algebraic groups you might have seen in earlier studies.
Group
Elements
n∈
m/n
+
m, n > 0
Operation
addition
Identity
0
Inverse
−n
Abelian
yes
multiplication
1
n/m
yes
multiplication
mod n
0
n−k
yes
multiplication
1
1/ x
yes
vector
addition
( 0, 0 )
( − a , −b )
yes
n
k ∈ {0,1, 2,..., n − 1}
− {0}
x nonzero real
2
( a, b ) ∈ 2
GL ( 2, )
a b 
c d 


ad − bc ≠ 0
matrix
multiplication
1 0 
0 1 


a b 
c d 


ad − bc = 1
matrix
multiplication
1 0 
0 1 


number
general linear
group
SL ( 2, )
special linear
group
 d
 ad − bc

 −c
 ad − bc
−b 
ad − bc 

a 
ad − bc 
 d −b 
 −c a 


Common Groups
Table 2
Notational Note: Repeated multiplication of an element g of a group by itself
result in powers of an element and are denoted by g n , n = 1, 2,... . When n = 0
we define g 0 as the identity g 0 = e .
Cyclic Groups (Modular
(Modular Arithmetic)
The most common and most simple of all groups are the cyclic groups,
groups
which are well-known to every child who has learned to keep time.
no
no
8
Section 6.2
Introduction to Groups
A finite cyclic group ( Z n , ∗) of order n is a group that contains an
Definition:
element g ∈ Z n called the generator of the group, such that
g ≡ {e, g , g 2 , g 3 ,..., g n −1} = Z n .
where “powers” of g are simply repeated multiplications7 of g ; that is
g 2 = g ∗ g , g 3 = g 2 ∗ g ,...
For example, the three rotational symmetries
triangle form a cyclic group
2
120
R
3
120
= R240 , R
3
{e, R120 , R240 }
with generator
of an equilateral
g = R120
(note that
= e ).
Cyclic groups also describe modular (or clock) arithmetic, which is the
type of arithmetic we carry out when keeping time on 24-hour timepiece,
where the numbers “wrap around” after 24 hours. However, unless you are
in the military, your clock lists hours from 0 to 11 so telling time is done, as
they say, modulo 12, as in 5 hours after 9 P.M. is ( 5 + 9 ) mod(12) = 3 A.M. .
This leads us to the cyclic group Z12 with elements
Z12 = {0,1, 2,3, 4,5, 6, 7,8,9,10,11 }
and the group operation on Z12 exactly what you do when you keep time, that
is
a ⊕ b = ( a + b ) mod12
where “mod 12” refers to computing a ⊕ b by computing
(a + b)
then taking
its remainder after dividing by 12. (We denote the group operation by ⊕ to
remind us it is addition, only reduced modulo 12.)
For example
2 = ( 9 + 5 ) mod12 which, related to a 12-hour clock, translates into 2 A.M is 5
hours after 9 P.M. The hours of the clock Z12 and keeping time using this
binary operation defines an Abelian group of order 12, called a cyclic group,
group,
whose Cayley table is shown in Table 3.
7
We use the word “multiplication” here, but keep in mind the group operation can mean any binary
operation, even addition.
9
Section 6.2
Introduction to Groups
⊕
0
1
2
3
4
5
6
7
8
9
10
11
0
1
0
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
0
2
3
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
0
0
1
1
2
4
4
5
6
7
8
9
10
11
0
1
2
3
5
6
7
8
5
6
7
8
6
7
8
9
7
8
9
10
8
9
10
11
9
10
11
0
10
11
0
1
11
0
1
2
0
1
2
3
1
2
3
4
2
3
4
5
3
4
5
6
4
5
6
7
9
10
11
9
10
11
10
11
0
11
0
1
0
1
2
1
2
3
2
3
4
3
4
5
4
5
6
5
6
7
6
7
8
7
8
9
8
9
10
Cayley table for the cyclic group of 12 elements
Table 3
Figure 3 shows various clocks that give rise to different cyclic groups.
The cyclic group Z 6 consists of elements Z 6 = {0, r1 , r2 , r3 , r4 , r5 } were as always
e is the identity map and rj is rotation of the clock by 60 j degrees, j = 1,...,5 .
This set, along with the binary operation of doing one operation after another
(function composition) forms a group with the following Cayley table. In other
to make the table read faster, we have replaced the angles of rotation rj by
the time on the hour hand, 1,2,3,… , 11.
10
Section 6.2
Introduction to Groups
Cyclic Groups n
Z2
Cyclic
Group
Of
Order
2
0
0
6
⊕
0
6
6
6
0
Z3
⊕
0
4
8
Cyclic
Group
of
Order
3
0
4
8
0
4
8
4
8
0
8
0
4
Z4
⊕
0
3
6
9
0
3
6
9
0
3
6
9
3
6
9
0
6
9
0
3
9
0
3
6
0
2
0
0
2
2
2
4
4
4
6
6
6
8
8
8
10
10
10
0
4
6
8
10
4
6
8
10
6
8
10
0
8
10
0
2
10
0
2
4
0
2
4
6
2
4
6
8
Cyclic
Group
of
Order
4
⊕
Z6
Cyclic
Group
of
Order
6
Z12
Cyclic
of
Order
12
See
Table 1
Cyclic Groups
Figure 3
11
Section 6.2
Introduction to Groups
Example 5 (Symmetries of a Square) Figure 4 shows the eight symmetries
of a square, called the octic group.
a) Is the octic group commutative? Hint: Compare products R270 a
and aR270 .
b) There are several subsets of the eight symmetries that form a group
in their own right. These are called subgroups of the octic group. Can you
find all ten of them?
Solution
a) The reader can check but R270 a ≠ aR70 . Hence, the octic group is not
commutative.
b)
The 10 subgroups of the octic group are
{e} , {e, v} , {e, h} , {e, d } , {e, a} , {e, R180 } , {e, R180 , v, h} , {e, R180 .d , a} , D4
The reader can visualize these symmetries and make Cayley tables for them.
(See Problem 16.) These subgroups form a partially ordered set and can be
put in the Hasse diagram shown in Figure 5.
12
Section 6.2
Motion
Symbol
No motion
e
Rotate 90
Counterclockwise
R90
Rotate 180
Counterclockwise
R180
Rotate 270
Counterclockwise
R270
Horizontal flip
h
Vertical flip
v
Anti-diagonal flip
a
Diagonal flip
d
Introduction to Groups
First and Final Positions
Symmetries of a Square
Figure 4
Section 6.2
13
Introduction to Groups
Hasse Diagram for the Subgroups of the Octic Group D4
Figure 5
Symmetry Groups of n -gons: Dihedral Groups
In Section 6.1 we saw how symmetries of a figure in the plane, which is
a rigid motion which leaves the figure unchanged, can create new symmetries
by following one symmetry after another. In this way, one creates an
“arithmetic” of symmetries, where the composition of symmetries plays the
role of multiplication, and the system contains identity elements, inverses and
all the goodies on an “arithmetic” system. In other words, a group of
symmetries, called the symmetry
symmetry group of the figure. Every figure no matter
how “non symmetric” has at least one symmetric group, namely the group
consisting only of the identity or ‘do nothing symmetry.”
The more
“symmetric” a figure the more elements in its symmetry group. In Section 6.1
we saw that the (non square) rectangle had four symmetries; namely rotations
14
Section 6.2
Introduction to Groups
of 0 and 180 degrees, and a horizontal and vertical flip about the midlines,
which constitute the Klein 4-group. On the other hand, the more “symmetric”
square has 8 symmetries in its symmetry group. (Can you find them?) Some
figures have both rotational and flip symmetries.
A polygon is called regular if all its sides have the same length and all its
angles are equal. An equilateral triangle is a regular 3-gon, a square is a
regular 4-gon, a pentagon is a regular 5-gon and so on. The symmetry group
of a regular n -gon, which has n rotational and n flip symmetries, for a total
of 2n symmetries, is called the dihedral group of the n -gon and denoted by
Dn Can you find the 10 symmetries of the dihedral group D5 of the pentagon
drawn in Figure 5?
Find the Symmetric Group D5
Figure 5
We are getting ahead of ourselves, but in addition to the complete dihedral
group of 10 symmetries of a pentagon, there is also a “smaller” group of five
rotation symmetries , called a subgroup,
subgroup which is a group in its own right, of
the larger group of 10 symmetries as well as a subgroup of the 5 flip
symmetries. Figure 6 shows commercial figures whose symmetry groups are
the dihedral groups D1 − D5 .
D1 one rotation (0 degrees), one vertical
flip
2 symmetries
D2 two rotations, two flips (horizontal
and vertical axes)
4 symmetries
15
Section 6.2
Introduction to Groups
D3 three rotations, three flips
6 symmetries
D4 four rotations, four flips
8 symmetries
D5 five rotations, five flips
10
symmetries
Figure with Dihedral Symmetry Groups
Figure 6
16
Section 6.2
Introduction to Groups
Problems
1. Do the following sets with given binary operations form a group? If it
does, give the identity element and the inverse of each element. If it does not
form a group, say why.
a)
b)
All even numbers, addition
{−1,1 } , multiplication
c)
d)
e)
All positive real numbers, multiplication
All nonzero real numbers, division
All 2 × 2 real matrices, matrix addition
f)
the four numbers 1, −1, i, −i where i = −1 is the unit
complex number, the binary operation is ordinary multiplication.
g)
{a, b, c}
with operation ∗ defined by the Cayley table
a
b
a
c
∗
a
b
c
c
a
c
b
b
c
b
a
2. (Finish the Group) Complete the following Cayley table for a group of
order three.
e
e
a
b
∗
e
a
b
a
a
b
b
3.
(Finish the Group) Complete the following Cayley table for a group of
order four without looking at the Cayley tables of the Klein 4- group or the
cyclic group of order 4 in the text.
∗
e
a
b
c
e
e
a
b
c
a
a
b
b
c
c
4. (Verification of a Group) Do the nonzero integers with the operation of
multiplication form a group?
17
Section 6.2
5.
Introduction to Groups
(Group You are Well Familiar) Show that {, +} is a group (i.e. the
integers with the operation of addition) is a group.
6.
(Property of a Group) Verify that for all elements a, b in a group the
identity
( ab )
−1
= b −1a −1 holds. Hint: Show that ( ab ) ( a −1b −1 ) = e .
General Properties of Groups
7.
8.
Show that a group has exactly one identity.
Show that every element in a group has no more than one inverse.
9. Show that in a group the identity
( ( ( ab ) c ) d ) = ( ab )( cd )
holds.
10. Let a, b, c are members of a set with a binary operation ∗ on the set. If
a = b , then the multiplication rule says ca = cb .
a) Show that in a group we can cancel the c .
b) Given an example of elements in the set 6 = {0,1, 2,3, 4,5} with
addition modulo 6, where cancellation does not hold.
11. (Cyclic Group) The cyclic group of order 6 describes the rotational
symmetries of a regular hexagon. Its Cayley table is shown in Table 4.
For notational simplicity the group elements are the number of degrees
required to map the hexagon back onto itself.
⊕
0
60
120
180
240
300
0
0
60
120
180
240
300
60
60
120
180
240
300
0
120
120
180
240
300
0
60
180
180
240
300
0
60
120
240
240
300
0
60
120
180
300
300
0
60
120
Cayley Table for 6
180
240
Table 4
a) What is the inverse of each element of the group?
b) The order of an element of a group is defined as the (smallest)
number of repeated operations on itself that results in the group identity.
What is the order of each element of the group?
18
Section 6.2
Introduction to Groups
c) Show that by taking repeated operations with itself of the element
240 the set of elements obtained is itself a group. Construct the Cayley
table of this group.
12. (Affine Group) The set G of all transformations from the plane to the p
lane of the form
x′ = ax + by + c
y′ = dx + ey + f
where a, b, c, d , e, and f are real numbers satisfying ad − bc ≠ 0 , is a group if we
define the group operation of performing one operation after the other, this
forms a group called the affine group.
group
a) What is the identity of the affine group? That is, what are the values
of a, b, c, d , e, f ?
b) What is the inverse of ( 0, 0 ) ?
13.. (Mod 5 Multiplication) Create the multiplication table for the integers
0,1, 2, 3, 4 where multiplication defined as mod ( 5) arithmetic. Show this defines
a group.
14.
(Mod 4 Multiplication) Create the multiplication table for the integers
0,1, 2,3 for modular arithmetic mod ( 4 ) and show that this does not define a
group.
In other that the numbers
0,1, 2,..., n − 1 forms a group under
mod ( n ) multiplication, it must be true that n is a prime number.
15.
(Subgroups of the Dihedral Group D4 )
A subgroup of a group is a subset
of the elements of a group which itself a group using the group operation of the
larger group. The Hasse diagram for the subgroups of the symmetries of a
square (i.e. the dihedral group ) is shown in Figure 6. The letter " F "
represents the identity element, the other letters represent rotations and
reflections of F . Interpret the rotations in the subgroups and make a Cayley
table for them.
16. (Subgroups of the Octic Group) Make a Cayley table for the subgroups of
the octic group.
{e, v}
b) {e, h}
c) {e, d }
a)
19
Section 6.2
Introduction to Groups
d) {e, a}
e) {e, R180 }
f) {e, R180 , v, h}
g) {e, R180 , d , a}
Hasse diagram for the Subgroups of D4
Figure 6
17. (Isomorphic Groups) Sometime two groups appear different but are really
the same group. The two groups in Figures 7, called Group A and Group B
look different, but are really the same, or what are called isomorphic groups.
Convince yourself the two groups are the same by making the substitution, or
isomorphism
⊕ → ⊗, 0 → i, 1 → a, 2 → b, 3 → c
that sends Group A into Group B.
20
Section 6.2
⊕
0
1
2
3
⊗
i
a
b
c
0
0
1
2
3
i
i
a
b
c
Introduction to Groups
1
1
2
3
0
Group A
2
2
3
0
1
a
a
b
c
i
b
b
c
i
a
3
3
0
1
2
c
c
i
a
b
Group B
18. (Harder to See Isomorphic Groups) Show that Group C and Group D are
isomorphic (the same group) by making the substitution
⊕ → ⊗, 0 → 1, 1 → 2, 2 → 4, 3 → 3
in Group C, and then interchanging the 3rd and 4th columns, followed by the 3rd
and 4th rows of the resulting table.
⊕
0
1
2
3
⊗
1
2
3
4
0
0
1
2
3
1
1
2
3
0
Group C
2
2
3
0
1
3
3
0
1
2
1
1
2
3
4
2
2
4
1
3
Group D
3
3
1
4
2
4
4
3
2
1