Download Document

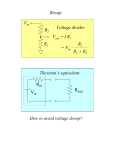
1
Chapter 5. Additional analysis
techniques
EMLAB
Contents
2
1. Introduction
2. Superposition
3. Thevenin’s and Norton’s theorems
4. Maximum power transfer
5. Application Examples
EMLAB
1. Introduction
3
Examples of equivalent circuits
To simply solution procedures, the
number of nodes or loops should be
minimized by replacing the original
circuits with equivalent ones.
EMLAB
Linearity
4
1 (t )
i1 (t )
Linear system
L
i2 (t )
Linear system
L
 2 (t )
Linear system
L
A1 (t )  B 2 (t )
Ai1 (t )  Bi2 (t )
A system satisfying the above statements is called as a linear system. Resistors,
Capacitors, Inductors are all linear systems. An independent source is not a linear
system.
All the circuits in the circuit theory class are linear systems!
EMLAB
5
Example of linear system
R1
output
Resistor
 1 (t ) -
1k
R1
i1 (t )
1k
1 (t )  i1 (t )  R1
input
  2 (t ) -
Capacitor
C1
1n
C1
i2 (t )
1n
1
 2 (t ) 
C
t
i
2
( ) d
0
EMLAB
6
Example 5.1
For the circuit shown in the figure, determine the output voltage Vout using linearity.
First, arbitrarily assume that the output voltage is Vout = 1 [V].
Vout  V2  1 [V ]
I1 
V1
 1 [mA]
3k
I2 
V2
 0.5 [mA]
2k
I 0  I1  I 2  1.5 [mA]
V1  4k  I 2  V2  3 [V ]
Vo  2k  I o  V1  6 [V ]
For the arbitrary assumption that Vout = 1 [V], the source voltage Vo should be 6 V.
Then from linearity, the actual output voltage should satisfy the following relation.
actual
actual
Vo : Vout  12 : Vout
 6 : 1  Vout
 2 [V ]
EMLAB
7
2. Superposition
Source superposition
VS
VS

VL

IS
I L,2
I L ,1
IL
Circuit
Circuit with voltage source
set to zero (Short circuited)
=
Circuit

VL ,1

Circuit with current source
set to zero(Open circuited)
+
Circuit

VL , 2

IS
I L  I L ,1  I L , 2
VL  VL ,1  VL , 2
•
•
•
Superposition is utilized to simplify the original linear circuits.
If a voltage source is eliminated, it is replaced by a short circuit connected
to the original terminals.
If a current source is eliminated, it is replaced by an open circuit.
EMLAB
Example 5.2
8
To provide motivation for this subject, let us examine the simple circuit below, in
which two sources contribute to the current in the network. The actual values of the
sources are left unspecified so that we can examine the concept of superposition.
=
 1  3k  i1  3k  (i1  i2 )  0
3k  (i2  i1 )  6k  i2   2  0
 6k
 3k

i 
1
 1 
i2  15k
+
 1  3k  i1  3k  (i1  i2 )  0
3k  (i2  i1 )  6k  i2  0
 6k
 3k

 3k   i1   1 

9k  i2    2 
3 1  1 
1

1 2    15k

 2 
 31   2 
  2 
2
 1
 3k   i1  1 

9k  i2   0 
i 
1
 1 
i2  15k
31 
 
 1
3k  i1  3k  (i1  i2 )  0
3k  (i2  i1 )  6k  i2   2  0
 6k
 3k

 3k   i1   0 

9k  i2    2 
i 
1
 1 
i2  15k
  2 
 2 
2

EMLAB
Example 5.3
9
Let us use superposition to find Vo in the circuit in Fig. 5.3a.
=
+
Io 
1
6k
 2 [mA] 
1
1

3k 6k
Vo  I o  6k  4 [V ]
2
[mA]
3
Vo 
6k
 3 [V ]  2 [V ]
3k  6k
Vo  Vo  Vo  6 [V ]
To verify the solution, we can apply the loop analysis technique.
I1  2 [mA]
1k  ( I1  I 2 )  2k  ( I1  I 2 )  3  6k  I 2  0
 I 2  1 [mA], Vo  6 [V ]
EMLAB
Example 5.4
10
Consider now the network in Fig. 5.4a. Let us use superposition to find Vo’.
+
=
 8k 


3   24 [V ]
V1  6
 8k  2k  7
 3

 6k  18
Vo  V1 
  [V ]
 6k  2 k  7
30
 10

Vo   k || 6k   2 [mA] 
[V ]
7
 3

Vo  Vo  Vo 
48
[V ]
7
EMLAB
Thevenin’s and Norton’s theorems
11
i
a
RV
+
-
VS
b


a

b
RI
IS
Single port network
  f (i )
  Ai  B  RThi  VTh
1. To find B, measure voltage with
i=0. (open circuit voltage)
2. To find A, measure the variation
of υ with i changing. (impedance)
i  g (i )
i  C  D  YNor  I Nor
1. To find D, measure current with υ =
0. (short circuit current)
2. To find C, measure the variation of
i with υ changing. (admittance)
EMLAB
How to construct Thevenin’s equivalent circuit
12
(1) Measure open circuit voltage (VOC) with a volt meter.
VS
I 0

VOC
Circuit
Input resistance of a
voltmeter is infinite.
RTH
V

=
IS

VOC

(2) Measure resistance (RTH) with sources suppressed. →Voltage
sources short circuited and current sources open circuited.
short
Circuit
Ω
Ohm meter
open
EMLAB
How to construct Norton’s equivalent circuit
13
(1) Measure short circuited current (ISH).
VS
Input resistance of an
ammeter is zero.
I SH
Circuit
A
=
IS
I SH
RTH
(2) Measure resistance (RTH) with sources suppressed.
→Voltage sources short circuited and current sources open circuited.
short
Circuit
Ω
Ohm meter
open
EMLAB
14
Example 5.6
Let us use Thévenin’s and Norton’s theorems to find Vo in the network below.
Vo 
Vo 
1
1
1

3k 6k
6k
 9  6 [V ]
3k  6k
 3 [mA]  6 [V ]
EMLAB
15
Example 5.7
Let us use Thévenin’s theorem to find Vo in the network in Fig. 5.9a.
VOC1 
6k
 12 [V ]  8 [V ]
3k  6k
VOC2  8  4k  2 [mA]  16 [V ]
VO 
RTh1  2k 
3k  6k
 4 [ k ]
3k  6k
RTh1  4 [k]
8k
 16  8 [V ]
16k
EMLAB
Example 5.9 : Circuits containing only dependent sources
16
→ Apply an external voltage or current source between the terminals.
Determine the Thévenin equivalent of the network in Fig. 5.11a at the terminals A-B.
V1 V1  2Vx V1  1


0
1k
2k
1k
V1 
Vx  1  V1
 Io 
5V1  2(1  V1 )  2  0
4
3
, Vx 
7
7
Vx 1  2Vx 1
3
3 15




 [mA]
1k
1k
2k 2k 7k 14
 RTh 
1 [V ] 14
 [ k ]
Io
15
EMLAB
17
Example 5.10
Let us determine at the terminals A-B for the network in Fig. 5.12a.
V1  2000 I x V1 V1  V2
 
0
2k
1k
3k
V2  V1 V2

 1m  0
3k
2k
Ix 
V1
1k
 3V1  6V1  2V1  2V2  5V1  2V2  0
2V2  2V1  3V2  6  2V1  5V2  6  0
V2 
10
V
10
[V ]  RTh  2  [k]
7
1m 7
EMLAB
Example 5.11 : Circuits containing both independent and dependent sources
18
In these types of circuits we must calculate both the open-circuit voltage
and short-circuit current to calculate the Thévenin equivalent resistance.
Let us use Thévenin’s theorem to find Vo in the network in Fig. 5.13a.
KCL for the super-node around the
12-V source is
VOC  12  2000 I x VOC  12 VOC


0
1k
2k
2k
V
I x  OC
2k
I x  0
4VOC  24  VOC  12  VOC  6VOC  36  0
I SC  
Vo 
12
2
[ k ]
3
1k
 18 [mA]
1
1k  1k  k
3
( 6 ) 
RTh 
VOC  6 [V ]
VOC
1
  [ k ]
I SC
3
3
18
 ( 6)   [V ]
7
7
EMLAB
19
Example 5.12
Let us find Vo in the network in Fig. 5.14a using Thévenin’s theorem.
I 2  2 [mA]
I1 
Vx
2000
Vx  4k  ( I1  I 2 )
Vx  2Vx  8  Vx  8 [V ]
VOC  2k  I1  3  11 [V ]
V  

 V 

 3  2k   I SC  x   0, Vx  4k   x  2m 
2000 

 2000

Vx  8 [V ]
I SC 
RTh 
Vo 
Vx
3
11

 4m  1.5m  [mA]
2000 2k
2
VOC
11

 2 [ k ]
I Sc 11 [mA]
2
6k
33
 11 
[V ]
6k  2 k
4
EMLAB
20
Example 5.14
Determine Vo in the circuit in Fig. 5.16a using the repeated application of
source transformation.
I SC 
12
3k  6k
 4 [mA], RTh 
 2k
3k
3k  6k
VOC  4m  2k  8 [V ], RTh  2k  2k  4k
I SC 
8
 2 [mA], RTh  4k
4k
VOC  4m  4k  16 [V ], RTh  4k
VO 
8k
 16k  8 [V ]
4k  4k  8k
EMLAB
21
4. Maximum Power Transfer
RS
PL  i 2 RL , i 
 PL 
Equivalent circuit of
a signal source

RS  RL
 2 RL
( RS  RL ) 2
We want to determine the value of RL that maximizes
this quantity. Hence, we differentiate this expression
with respect to RL and equate the derivative to zero.
2
PL
2 ( RS  RL )  2 RL ( RS  RL )

RL
( RS  RL ) 4
2
Maximum power transfer condition :
( RS  RL )
0
( RS  RL )3
RL  RS
EMLAB
22
Example 5.16
Let us find the value of RL for maximum power transfer in the network in Fig. 5.20a
and the maximum power that can be transferred to this load.
RL  RTh  4k 
6k  3k
 6k 
6k  3k
3k  ( I 2  I1 )  6k  I 2  3  0, I1  2m
I2 
1
[mA]
3
VOC  4k  I1  6k  I 2  8  2  10 [V ]
2
 10 
 PL  
 6k  4.17 [mW ]
 12k 
EMLAB
23
Example 5.17
Let us find RL for maximum power transfer and the maximum power transferred
to this load in the circuit in Fig. 5.21a.
VOC  2000 I x
V
V
 4m  OC  0, I x  OC
4k
2k
2k
VOC  8 [V ]
I x  0 x  I SC  4 [mA]
RTh 
VOC
 2 k
I SC
2
 8 
 PL  
 6k  2.67 [mW ]
 12k 
EMLAB