Download The Making of Quantum Theory

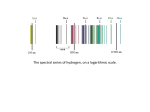
Max Planck (1858 – 1947)




Founder of the quantum theory
Proposed that radiation is emitted in discreet packets called quanta
(singular quantum)
Energies associated with these quanta are proportional to the
frequencies of the emitted radiation.
He formulated the following equation: E = hf
Where E is the energy of radiation
h is Planck’s constant (6.626 x 10-34 Js)
f is the frequency of the radiation.
Albert Einstein (1879 – 1955)


Theory of relativity
Theory of the photoelectric effect – Noble prize in 1921
The photoelectric effect
Einstein viewed electromagnetic radiation as beams of photons – each photon
is a little packet of energy with the value E = h f. Frequency is equal to the
speed of light divided by the wavelength of the radiation in question and
thus this equation can be rearranged to read:
E=hc

Using this equation he set about trying to explain why high frequencies of
photons, whereas they caused more electrons to be ejected from the
surface of the solid, did not change the energy each electron possessed.
This equation, which uses the principle of the law of conservation of energy,
won Einstein his noble prize.
Note: The theories of Planck and Einstein were the first steps in the
development of the quantum theory.
Louis DeBroglie


French physicist
Received the Nobel Prize in physics in 1929.
Louis de Broglie proposed the wave-particle duality of light. This simply put,
is the phenomenon that waves behave both like a particle and as a wave. De
Broglie proposed that both light and matter obey the equation:
 = h
mv
Where: λ is the de Broglie wavelength
m is the mass which when multiplied by velocity is momentum
h is Planck’s constant
Sample problem:
Calculate the de Broglie wavelength of an electron traveling at a speed of
3.0 x 106 m/s ( 1 % the speed of light).
v = 3.0 x 106 m/s
m = 9.11 x 10-31 Kg
h = 6.626 x 10-34 J s
Note: The wavelength of the electron falls in the X-ray region of the
electromagnetic spectrum. (1 x 10-9 m = 1 nanometer)
Neils Bohr 1885 - 1962




Danish physicist
First quantum model of the atom
Formulated a description of the hydrogen atom that explained its
light spectra
Using Einstein’s work and Planck’s work – Bohr related the colour of
hydrogen’s spectra to wavelength and then wavelength to energy.
Bohr postulated that the colours of the Hydrogen spectra were discreet
bands of colour – the photons causing the electrons to be released when
excited electrons drop back from higher energy levels at which they exist.
Bohr showed that electrons are quantized. He demonstrated that the only
possible energies of electrons in his orbital/energy levels would be given by
the equation:
En =
- 1311 KJ/mol
n2
The En values given by this equation corresponds to the energy states of
electrons in a hydrogen atom.
These stationary states/energy levels are known as the ground state and
excited states.
The Hydrogen Spectrum of Light
When an electron makes a transition form a higher energy state to a lower
energy state each transition is accompanied by the emission of a photon
having a wavelength that corresponds with the electromagnetic spectrum.
Radio waves, microwaves, infrared light, visible light, ultraviolet light, X-rays
and gamma rays are all forms of electromagnetic radiation.
When electrons are passed through a gas, radiation is emitted at discreet
wavelengths. This is called a line spectrum. If we are examining a gas
consisting of individual atoms then we call the spectra atomic emission
spectra.
In 1885 Johann Balmer – an amateur Swiss scientist – developed a
mathematical relationship that could explain and predict the visible
spectrum of hydrogen. Johannes Rydberg – a Swedish physicist – using the
work of Balmer developed an equation that related all the wavelengths of
lines produced in the electromagnetic spectrum of Hydrogen. The equation
is as follows:
1 = (1.097 x 107 m-1) ( 1 –

n12
1)
n22
Where 1.097 x 107 is the Rydberg constant = RH
n1 is the series type
n2 is the energy level the electron is transitioning from.
Using the Rydberg equation, we can look at the Balmer series and determine
the wavelength of visible light emitted by Hydrogen.
As mentioned earlier: The hydrogen electron has a variety of transitions
from different energy levels. The line spectra that we see is only visible in
the visible region of the electromagnetic spectrum. However, there are
transitions that occur in ultra violet and infrared region of the spectrum.
Series type n1
n1 = 1
n1 = 2
n1 = 3
n1 = 4
Series Name
Lyman series
Balmer series
Paschen series
Brackett series
Region of spectrum
Ultra-violet light
Visible spectra of hydrogen
Infrared light
Infrared light
THE BALMER SERIES
COLOUR
Red
Green
Blue
Indigo
Violet
n2
3
4
5
6
7
TRANSITION
3 2
4 2
52
62
72
WAVELENGHT
656.2 nm
489.1 nm
434.0 nm
410.1 nm
369.6 nm
It is possible to calculate the transitions for other series (Lyman, Paschen,
Brackette) using the general Rydberg equation:
1 = RH ( 1
–
2

n1
1)
n22
Sample problem:
Calculate the frequency and wavelength of transition between n3 and n2 in
the Balmer series.
n1 = 2 ; n2 = 3
Homework:
Calculate the rest of the wavelengths for the light emitted in the Balmer
series.
Calculate at least one transition in each of the Lyman and Paschen series.
Note: Lyman series: any level  ground state
Paschen series: any level  level 3
THE HYDROGEN SPECTRUM ( E = -1311 kJ/mol/n2)
-36.4
-52.4
-81.94
-145.67
-327.75
-1311
A continuous spectrum is produced when white light is passed through a
prism. The result is line a rainbow, where ROYGBIV can be seen.
Absorption Spectra:
In order to excite an electron a certain amount of energy is required (at a
particular wavelength) corresponding to the differences between the energy
levels. For example, an object that absorbs blue, green and yellow light will
appear red when viewed under white light.
Uses: to identify elements present in a gas or liquid, for example elements in
stars and other gaseous objects which cannot be measured directly.
Emission Line Spectra:
This is the opposite of absorption line spectra. The energy released when an
electron falls back down to the ground state (at a particular wavelength)
corresponding to the difference between the energy levels.
Source: http://www.daviddarling.info/encyclopedia/C/contspec.html
NEILS BOHR’ S ATOMIC MODEL
There were two main improvements to the historical atomic model.
1.
The number of electrons at each principle energy level became known:
# electrons = 2n2 where n is the principle energy level
evidence/reasoning - ascertained from the intensity of the spectral
lines of hydrogen.
2. Electrons must be located in levels of specific and fixed energies
(orbits). For the hydrogen the energy at each level can be calculated
using the equation given above.
Evidence/Reasoning – given that hydrogen gave off four very distinct
bands in the spectrum he used Einstein’s and Planck’s work that related
first colour to wavelength and then wavelength to Energy, i.e. If the
colours were discreet bands of colour the photons must have discreet
amounts of energy, since this energy was released when excited electrons
dropped from higher energy to lower energy, the electrons must have
specific energy levels at which they must exist and not in between.
Although Bohr’s model did much to further the understanding of the
atom and energies there would be other discoveries that would
necessitate change in his model. The wave-particle duality of electron
would change the nature of an atom forever… do stay tuned.
BOHR MODEL'S LIMITATIONS
1. The electron is a particle whose position and motion can be
specified at a given time.
2. An electron moves in an orbit having a fixed radius.
3. Bohr's experimental evidence only agrees with an one-electron
atom (Hydrogen)
… in addition to this, studies reveal that:
Electrons behave as particles in some experiments while in other
experiments they behave as WAVES
In order to describe the motion of an electron in an atom, both the
electron's wave and particle nature must be taken into account.
HEISENBERG UNCERTAINTY PRINCIPLE states that due
to the dual nature of the electron it is impossible to determine both
its position and energy at the same time.
ORBITALS
Erwin Schrodinger, 1926, used wave equations and calculations
that predict the CHANCE of an electron showing up in a particular
region of space around the nucleus. This calculated region of
space is called an Orbital. Electrons are moving about like bees
within the orbital.
SOME IMPORTANT DEFINITIONS
AUFBAU PRINCIPLE – electrons go into the lowest energy level
and fill them in order of increasing energy.
PAULI EXCLUSION PRINCIPLE – an orbital can hold a
maximum of two electrons. But an orbital can be empty or have
one electron. (0,1,2)
HUND'S RULE – electrons in the same sublevel or orbitals will
not pair up until all the orbitals of the sublevel are at least halffilled.
ELECTRONIC CONFIGURATION – distribution of electrons
among the various orbitals.
Energy Level Diagram
n=4
n=3
n=2
n=1
Nucleus