Download Review - Liberty High School

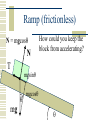
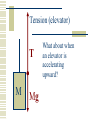
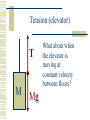
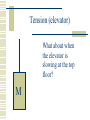
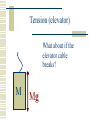
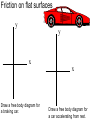
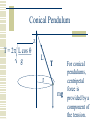
Newton’s Laws
What is Force?
 A push or pull on an object.
 Unbalanced forces cause an object to
accelerate…



To speed up
To slow down
To change direction
 Force is a vector!
Types of Forces
 Contact forces: involve contact between
bodies.

Normal, Friction
 Field forces: act without necessity of contact.

Gravity, Electromagnetic, Strong, Weak
 Question: Is there really any such thing as a
contact force?
Forces and Equilibrium
 If the net force on a body is zero, it is in
equilibrium.
 An object in equilibrium may be moving
relative to us (dynamic equilibrium).
 An object in equilibrium may appear to be at
rest (static equilibrium).
Galileo’s Thought Experiment
Galileo’s Thought Experiment
This thought experiment lead to
Newton’s First Law.
Newton’s First Law
 The Law of Inertia.
 A body in motion stays in motion in a
straight line unless acted upon by an
external force.
 This law is commonly applied to the
horizontal component of velocity, which is
assumed not to change during the flight of a
projectile.
Newton’s Second Law
 A body accelerates when acted upon by a net
external force
 The acceleration is proportional to the net (or
resultant) force and is in the direction which
the net force acts.
 This law is commonly applied to the vertical
component of velocity.
 SF = ma
Newton’s Third Law
 For every action there exists an equal and
opposite reaction.
 If A exerts a force F on B, then B exerts a
force of -F on A.
Commonly Confused Terms
 Inertia: or the resistance of an object to being
accelerated
 Mass: the same thing as inertia (to a physicist).
 Weight: gravitational attraction
inertia = mass  weight
Sample Problem – 1st Law
 Two forces, F1 = (4i – 6j + k) N and F2 = (i – 2j - 8k) N, act
upon a body of mass 3.0 kg as it is moving at constant speed.
What do you know must be true?
Sample Problem – 2nd Law
 Two forces, F1 = (4i – 6j + k) N and F2 = (i – 2j - 8k) N, act
upon a body of mass 3.0 kg. No other forces act upon the body
at this time. What do you know must be true?
Sample Problem – 3rd Law
 A tug-of-war team ties a rope to a tree and pulls hard
horizontally to create a tension of 30,000 N in the rope. Suppose
the team pulls equally hard when, instead of a tree, the other end
of the rope is being pulled by another tug-of-war team such that
no movement occurs. What is the tension in the rope in the
second case?
Working a
nd
2
Law Problem
 Working Newton’s 2nd Law Problems is best
accomplished in a systematic fashion.
 The more complicated the problem, the more
important it is to have a general procedure to
follow in working it.
nd
2
Law Procedure
1. Identify the body to be analyzed.
2. Select a reference frame, stationary or moving, but
not accelerating
3. Draw a force or free body diagram.
4. Set up ΣF = ma equations for each dimension.
5. Use kinematics or calculus where necessary to
obtain acceleration.
6. Substitute known quantities.
7. Calculate the unknown quantities.
Sample Problem
 A 5.00-g bullet leaves the muzzle of a rifle with a speed of 320
m/s. The bullet is accelerated by expanding gases while it travels
down the 0.820 m long barrel. Assuming constant acceleration
and negligible friction, what is the force on the bullet?
Sample Problem
 A 3.00 kg mass undergoes an acceleration given by a =
(2.50i + 4.10j) m/s2. Find the resultant force F and its
magnitude.
Normal force
 The force that keeps one object from
invading another object.
 Our weight is the force of attraction of our
body for the center of the planet.
 We don’t fall to the center of the planet.
 The normal force keeps us up.
Normal Force
on Flat surface
Normal Force
on Flat surface
N
mg
N = mg for objects
resting on horizontal
surfaces.
Ramp (frictionless)

Ramp (frictionless)
N = mgcos
N
mgsin

mg
The normal force is
perpendicular to angled
ramps as well. It’s usually
equal to the component
of weight perpendicular
to the surface.
mgcos

Ramp (frictionless)
What will acceleration
be in this situation?
N
SF= ma
mgsin = ma
mgsin gsin = a
N = mgcos

mg
mgcos

Ramp (frictionless)
N = mgcos
N
How could you keep the
block from accelerating?
T
mgsin

mg
mgcos

Tension
 A pulling force.
 Generally exists in a rope, string, or
cable.
 Arises at the molecular level, when a
rope, string, or cable resists being pulled
apart.
Tension (static 2D)
The horizontal and vertical components of the
tension are equal to zero if the system is not
accelerating.
30o
45o
1
2
3
15 kg
Tension (static 2D)
The horizontal and vertical components of the
tension are equal to zero if the system is not
accelerating.
30o
T3
mg
45o
1
2
3
15 kg
SFx =
T1 0
T2
SFy =
T3 0
Tension (elevator)
What about when
an elevator is
accelerating
upward?
M
Tension (elevator)
T
M
Mg
What about when
an elevator is
accelerating
upward?
Tension (elevator)
M
What about when
the elevator is
moving at
constant velocity
between floors?
Tension (elevator)
T
M
Mg
What about when
the elevator is
moving at
constant velocity
between floors?
Tension (elevator)
What about when
the elevator is
slowing at the top
floor?
M
Tension (elevator)
T
M
Mg
What about when
the elevator is
slowing at the top
floor?
Tension (elevator)
What about if the
elevator cable
breaks?
M
Tension (elevator)
What about if the
elevator cable
breaks?
M
Mg
Pulley problems
Magic pulleys simply bend the coordinate system.
m1
m2
Pulley problems
Magic pulleys simply bend the coordinate system.
N
T
T
m1g
-x
m1
SF = ma
m2g
= (m1+m2)a
m2g
m2
x
Pulley problems
All problems should be started from a force
diagram.

m2
Pulley problems
Tension is determined by examining one block
SF2 = m2a
or the other
m2g - T = m2a
T
T
N
m1g

m2
SF1 = m1a
T-m1gsin = m1a
m2g
Atwood machine
m2
m1
 A device for measuring g.
 If m1 and m2 are nearly the same,
slows down freefall such that
acceleration can be measured.
 Then, g can be measured.
Atwood machine
T
m2
T
 A device for measuring g.
 If m1 and m2 are nearly the same,
slows down freefall such that
acceleration can be measured.
 Then, g can be measured.
m1
m1g
m2g
SF = ma
m2g-m1g = (m2+m1)a
Easy Problem
How fast will the block be sliding at the bottom of the
frictionless ramp?
5.0 kg
20o
L = 12 m
Easy Problem
How high up the frictionless ramp will the block slide?
v = 12.0 m/s
5.0 kg
20o
Problem
Describe accelerationModerate
of the 5 kg block.
Table and pulley are
magic and frictionless.
1.0 kg
20o
Friction
 Friction opposes a sliding motion.
 Static friction exists before sliding
occurs
 (fs  sN).
 Kinetic friction exists after sliding
occurs
 fk = kN
Friction on flat surfaces
y
y
x
Draw a free body diagram for
a braking car.
x
Draw a free body diagram for
a car accelerating from rest.
Test this hypothesis
 Hypothesis: Static friction is, in general, greater
than kinetic friction for the same two surfaces.
 In your lab groups, use a labquest and force
sensor to prove or disprove this hypothesis.
 Calculate the coefficients of static and kinetic
friction between the two surfaces you use in
your experiment.
 When you have demonstrated success to me,
plan your demonstration for next class.
Friction on a ramp

Sliding down

Sliding up
Friction is always parallel to surfaces….
A 1.00 kg book is held against
a wall by pressing it against the
wall with a force of 50.00 N.
What must be the minimum
coefficient of friction between
the book and the wall, such that
the book does not slide down
the wall?
f
F
N
W
(0.20)
Problem #1
Assume a coefficient of static friction of 1.0 between tires and
road. What is the minimum length of time it would take to
accelerate a car from 0 to 60 mph?
Problem #2
Assume a coefficient of static friction of 1.0 between tires and road and a
coefficient of kinetic friction of 0.80 between tires and road. How far
would a car travel after the driver applies the brakes if it skids to a stop?
Centripetal Force
 Inwardly directed force which causes a body
to turn; perpendicular to velocity.
 Centripetal force always arises from other
forces, and is not a unique kind of force.

Sources include gravity, friction, tension,
electromagnetic, normal.
 ΣF = ma
 a = v2/r
 ΣF = m v2/r
Highway Curves
z
R
Friction turns the vehicle
N
r
mg
Normal force turns the vehicle
Conical Pendulum
z
T = 2p L cos 
g
L
r
T
For conical
pendulums,
centripetal
force is
mg provided by a
component of
the tension.
Sample problem
• Find the minimum safe turning radius for a car traveling
at 60 mph on a flat roadway, assuming a coefficient of
static friction of 0.70.
Sample problem
• Derive the expression for the period of a conical
pendulum with respect to the string length and radius of
rotation.
Sample problem
• Derive the expression for the period best banking angle
of a roadway given the radius of curvature and the likely
speed of the vehicles.
Non-uniform Circular Motion
 Consider circular motion in which either speed of
the rotating object is changing, or the forces on the
rotating object are changing.
 If the speed changes, there is a tangential as well as
a centripetal component to the force.
 In some cases, the magnitude of the centripetal
force changes as the circular motion occurs.
Sample problem
You swing a 0.25-kg rock in a vertical circle on a 0.80 m long rope
at 2.0 Hz. What is the tension in the rope a) at the top and b) at
the bottom of your swing?
Sample problem
A 40.0 kg child sits in a swing supported by 3.00 m long chains. If
the tension in each chain at the lowest point is 350 N, find a) the
child’s speed at the lowest point and b) the force exerted by the
seat on the child at the lowest point.
Sample problem
A 900-kg automobile is traveling along a hilly road. If it is to
remain with its wheels on the road, what is the maximum speed it
can have as it tops a hill with a radius of curvature of 20.0 m?