Download Here

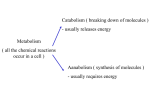
USSKAR-30-2 : Practice & Communication of Science
LDH Investigation: - Assay, Investigations & Analysis
Background
Lactate Dehydrogenase (LDH) is a ubiquitous enzyme that exists in various isoforms, depending on its overall role in the
metabolism of the cell in which it is expressed. Heart muscle LDH contains isoenzymes which are richer in H type
subunits, skeletal muscle contains LDH isoenzymes richer in M type subunits.
In this practical we shall be exploring issues such as differences between the H4 and the M4 isoenzymes in relation to
Km, pH-dependence and inhibition by other molecules.
It is worth considering whether any differences in behaviour between the isoenzymes represent an adaptation to serve
the way that particular tissue functions. To appreciate differences in the way pyruvate and lactate are metabolised by
different tissues let’s consider skeletal muscle, heart and brain. In skeletal muscle the reserves of glycogen are there
solely to power contraction, especially while the blood supply is still insufficient to support the aerobic oxidation of
glucose. Because anaerobic glycolysis gives a low yield of ATP, a relatively large amount of glucose carbons flow into the
pathway so concentration of pyruvate and lactate are high. Heart and brain by contrast are highly aerobic tissues which
are normally not allowed to become anaerobic. Aerobic glycolysis in heart muscle generates pyruvate which is
converted to acetyl CoA which then enters the citric acid cycle to be completely oxidised to CO 2 and water. Heart muscle
is also well able to utilise lactate, which has diffused into the blood from skeletal muscle, as fuel. The lactate is converted
back to pyruvate and then to acetyl CoA to be efficiently and completely oxidised as described above (liver on the other
hand also takes up lactate but converts most of it back to glucose via the gluconeogenesis pathway). Brain is an unusual
tissue in that it is normally only able to utilise glucose as fuel; this is converted to pyruvate through aerobic glycolysis
and then completely oxidised as in heart. In both heart and brain the conversion of pyruvate to lactate is a metabolic
‘dead end’, depriving the oxidative pathways of substrate and serving no useful function beyond regenerating NAD.
The Assay
The activity of LDH is assayed via the following reaction.
Pyruvate
Lactate
Lactate Dehydrogenase
NADH
NAD+
The oxidation of the NADH to NAD+ results in a decrease in absorbance at 340nm allowing the process to be followed
spectrophotometrically.
Basic Assay Method
Switch on the spectrophotometer, set the wavelength to 340nm. Place a blank, Tris-filled cuvette in the
spectrophotometer and zero using the CAL button. You just need to do this once.
a) For the assay, pipette the following into a cuvette:
 Tris buffer, 100mM pH 7.4
2.7 mL (may differ if adding inhibitors)
 NADH, 6mM
0.1 mL
 LDH purified from heart or skeletal muscle
0.1 mL
b) Mix well with a pastette and place in the spectrophotometer. Select start on the laptop.
c) Add to the cuvette 0.1ml, 30mM sodium pyruvate, pH 7.4; mix well immediately with a pastette and record for 3 min.
d) The easiest way to measure a rate from a recording is to note the absorbances at two points separated by one minute
(make sure the recording is linear over that section) then take one absorbance from the other to give Ab change/min.
Investigations
We have available to us…



Two LDH isoenzymes (bovine muscle and bovine heart)
Oxalic and oxamic acids (potential inhibitors of the enzyme)
Buffers of varying pH
Each group of 3 students will be assigned one of the following questions …
1.
2.
3.
4.
5.
6.
How do the Km values for muscle and heart compare?
How do the pH optima for muscle and heart compare?
Is oxalic acid an inhibitor of muscle LDH and, if so, what is its Ki?
Is oxalic acid an inhibitor of heart LDH and, if so, what is its Ki?
Is oxamic acid an inhibitor of muscle LDH and, if so, what is its Ki?
Is oxamic acid an inhibitor of heart LDH and, if so, what is its Ki?
Analysis
Rate calculations (all investigations)
In the reaction system used, a fixed amount of enzyme (typically 0.1 ml of stock) was followed in a fixed final volume (3
ml) and other factors affecting the rate of the reaction were varied (eg pH, substrate concentration, inhibitor
concentration). We are interested in relative changes in activity, so we can use a straightforward calculation of change in
absorbance rate directly from the recordings rather than anything fancy like µmoles substrate/mg enzyme.
There are two things to note. Firstly, the change in absorbance rate (for a suitably linear section of the recording) is
simply the difference in absorbance between two points divided by the time interval between them. The units will be
either Ab units/sec or Ab units/min, depending on your choice of time units (just be consistent). Secondly, in the current
assay, absorbance decreases with time (as the NADH is consumed); although this will mean that rates are negative, you
can just ignore the sign as it makes no difference to the analysis.
Basic Kinetics; Km (all except pH dependence)
Here is a typical saturation curve showing the relationship between substrate concentration and reaction rate…
There are two values that help define this curve; the maximum rate, Vmax, at which the enzyme can work under
conditions of ‘infinite’ substrate availability and the substrate concentration at which half this rate is achieved, the Km.
This can be quite difficult to estimate from a curve, so the data are transformed to make the relationship linear and
permit the straightforward estimation of Km and Vmax. A common transformation is the Lineweaver-Burk plot – a plot of
1/[S] vs 1/v.
You can download and use the kinetics spreadsheet from the website
(http://www.rags.profile.ac.uk/dl/UWE_KAR/exex/) to calculate the Km value for each ‘run’ of your experimental
procedure (if that is what you are investigating). Just make sure the substrate concentrations are correct (and the
correct way around) and type your rates into the corresponding green cells.
1.
How do the Km values for muscle and heart compare?
Assumption: You measured the rate of the enzymic reaction across a range of substrate concentrations for both heart
and muscle LDH. You did this several times for each enzyme (ie several experimental ‘repeats’).
Analysis: For each ‘repeat’ of one particular enzyme across the range of substrate concentrations, calculate its Km using
the above spreadsheet (you could use one of the Lineweaver-Burk plots to illustrate the poster). You can then calculate
the mean and SD for the two enzymes and perhaps plot them as a simple bar chart with error bars. For the statistical
analysis, use an unpaired t-test (since the muscle/heart ‘repeat’ estimations you carried out are not ‘paired’ in any
meaningful sense). The Null Hypothesis, of course, is that the Km values for each type of enzyme do not differ. What did
you find and how does it compare to previously published literature? Is there a theoretical basis for any significant
difference you found?
2.
How do the pH optima for muscle and heart compare?
Assumption: You measured the rate of the enzymic reaction across a range of buffer pH for both heart and muscle LDH.
You did this several times for each enzyme (ie several experimental ‘repeats’).
Analysis – is there a pH optimum for each enzyme? If you looked at the effect of pH on the reaction then we would
expect there to be a pH optimum provided a sufficient range of pH buffers was considered. This means that a plot of
rate (y) versus pH (x) would not be linear, so we cannot just do a regression analysis. Since you used discrete ‘categories’
of pH, an ANOVA might be the best approach.
In Minitab, either put all your rate data for one enzyme in one column with an adjacent column containing the pH or put
the rate data for each pH in separate columns; choose Stat > ANOVA > One-way, and choose the appropriate data layout
from the drop-down menu. Put the Responses (or Response/Factor combination) in the appropriate boxes to do the
analysis. Click the Comparisons… button and choose Tukey to test which, if any, pH values are significant (an alternative
approach would be to find the pH that gave the highest mean, then use this as the ‘control’ value and choose Dunnett
via the Comparisons… button).
The Null Hypothesis, of course, is that the rates found in different pH buffers (for a particular enzyme) do not differ.
What did you find and how does it compare to previously published literature? Is there a theoretical basis for any
significant difference you found?
Analysis – do the pH optima for the two enzymes differ? This probably requires a slightly different approach (unless
only one pH for each enzyme above stood out as significantly different, and this differed for each enzyme). Each repeat
of your experiment (ie one type of enzyme over a range of pH buffers) will identify the pH at which the maximum rate
was observed. You can note that pH for each repeat (noting the type of enzyme as well). You will end up with a set of,
say, five pH values for each enzyme (assuming you did the experiment five times). You could then carry out an unpaired
t-test (though there are probably a few assumptions being made here about how the data distribute). The Null
Hypothesis, of course, is that the pH optima for each type of enzyme do not differ. What did you find and how does it
compare to previously published literature? Is there a theoretical basis for any significant difference you found?
3-6. Is oxalic acid/oxamic acid an inhibitor of heart/muscle LDH?
Assumption: You measured the rate of the enzymic reaction across a range of substrate (pyruvate) concentrations in the
presence or absence of a concentration of potential inhibitor (oxalic acid or oxamic acid) for either heart and muscle
LDH. You will have done this several times (ie several experimental ‘repeats’).
Analysis : You need to determine the relationship between LDH activity and pyruvate concentration in the presence and
absence of the inhibitor. So, follow the guidance for Basic Kinetics; Km (all except pH dependence), above, determining
the Km and Vmax of the LDH for each ‘run’ using the ‘kinetics’ spreadsheet. You will then have a set of Km and Vmax values
in the absence of inhibitor and in the presence of inhibitor. You can then compare (using an unpaired t-test) the Km
values in the presence and absence of inhibitor, and then Vmax values in the presence and absence of inhibitor. You could
also get the mean (and SD) for each conc of pyruvate in the presence or absence of inhibitor and plot those as a
Lineweaver-Burk plot with appropriate lines of best fit (for the poster). From the results of the analysis and the shape of
the L-B plot you can a) determine if the potential inhibitor is significantly changing either (or both) Km and Vmax and b)
infer what sort of inhibition it is (competitive, non-competitive, uncompetitive, mixed).
(NB, the calculation of Ki - as suggested in the original question - is fairly involved, and varies according to the pattern of
inhibition. To be fair in terms of workload, we will not attempt this.)
What did you find and how does it compare to previously published literature? Is there a theoretical basis for any
significant difference you found?