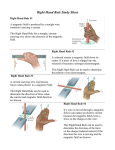
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Electrical resistance and conductance wikipedia , lookup
Electrostatics wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Magnetic monopole wikipedia , lookup
Magnetic field wikipedia , lookup
Field (physics) wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromagnetism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Superconductivity wikipedia , lookup
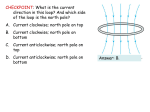
Physics 11b Lecture #12 Sources of the Magnetic Field S&J Chapter 30 What We Did Last Time b Lorentz force on current FB = I ∫ ds × B a Simplifies to FB = IL × B if the B field is uniform Torque on a current loop in a B field τ = IA × B Current loop looks like a magnetic dipole µ = IA 1 nq RH IB Hall effect ∆VH = t Magnetic fields are created by electric current RH ≡ µ0 Ids × rˆ Biot-Savart Law dB = 4π r 2 µ0 I B field by an infinite straight-line current B = 2π a Today’s Goals Continue with Biot-Savart law Calculate B field created by a straight-line current Force between two currents Ampère’s Law Integral form of Biot-Savart law Useful in solving magnetic field problems Examples: thick wire, infinite current sheet, solenoid Magnetic flux and Gauss’s law of magnetism Magnetism in matter Biot-Savart Law B field due to current in a short piece of wire is given by the Biot-Savart Law dB I µ0 Ids × rˆ dB = 4π r 2 ds dB is perpendicular to both ds and r Size of dB depends on the angle between ds and r Ids sin θ 2 r Ids r2 θ I ds dB = 0 r Straight-Line Current Current I flows in an infinitely-long straight wire B field at distance a from the wire? y µ0 Ids × rˆ µ0 Idx sin θ dB = zˆ dB = 2 2 4π r 4π r We move ds from x = −∞ to +∞ r a r and θ changes as we go θ r 2 = a2 + x2 a a sin θ = tan θ = − r x x I z ds We can integrate with x, r, or θ Æ which one is the easiest? Straight-Line Current Easiest to integrate if switch from dx to dθ adθ a y x=− dx = tan θ sin 2 θ dB a Also r = sin θ a µ0 Idx sin θ dB = 4π r2 µ0 I sin θ dθ I = z a 4π µ0 I π µ0 I µ0 I π sin θ dθ = B= [ − cos θ ]0 = ∫ 0 4π a 4π a 2π a r θ x ds B field goes around the wire and decrease as 1/a B Field Around Current B field circles around (infinitely-long) current Direction of B follows right-hand rule Magnitude B decreases as µ0 I B= 2π r cf. E field created by infinitely-long linear charge distribution was λ charge E= density (C/m) 2πε 0 r Similar, but E points outward, B rotates around B r I Force Between Currents Run two straight wires in parallel I1 I2 µ0 I1 B= 2π a F feels the force a Parallel currents attract each other I2 creates rotating B field µ0 I1 I 2 A F = I 2L × B = 2π a I1 If I1 and I2 flow in opposite directions, they repel each other For I1 = I 2 = 1A and a = A = 1m µ0 (1A) 2 (1m) F= = 2 × 10−7 N 2π (1m) This is in fact how Ampere is defined A Ampère’s Law µ0 I The denominator of B = looks like the circumference 2π r of a circle ds If we draw a circle around the current and line-integrate r µ0 I v∫ B ⋅ ds = v∫ 2π r ds = µ0 I This is generalized to Ampère’s Law For any closed path, the line integral of the magnetic field is v∫ B ⋅ ds = µ I 0 where I is the total current passing through any surface bounded by the closed path Ampère’s Law Ampère’s Law follows Biot-Savart Law Same way as Gauss’s Law follows Coulomb’s Law It’s useful when a symmetry of the problem helps us to predict at least the direction of the B field Example: long wire with finite thickness Current I flows uniformly through a cylindrical wire R I What’s the B field outside and inside of the wire? Thick Wire Inside the wire Circle with radius r1 < R encircles current π r 2 Ir 2 I 1 2 = 12 πR R Ampère’s Law µ0 I Ir12 B= r 2 1 v∫ B ⋅ ds = 2π r1B = µ0 R 2 2π R R r1 r2 Outside the wire Circle with radius r2 > R encircles I Ampère’s Law µ0 I = B v∫ B ⋅ ds = 2π r2 B = µ0 I 2π r2 Same result as a thin wire Thick Wire Combining, we find ⎧ µ0 I ⎪⎪ 2π R 2 r r ≤ R B=⎨ ⎪ µ0 I r>R ⎪⎩ 2π r R r1 B(r ) r2 µ0 I 2π R B∝ B∝r R 1 r This part is same as thin wires r Infinite Current Sheet Infinite sheet carries current density Js A/m B fields are parallel to the sheet opposite directions above and below Draw a rectangle and apply Ampère v∫ B ⋅ ds = 2BA = µ I A 0 s B B= µ0 I s 2 Uniform B field is created B A Two Infinite Current Sheets What if we had two current sheets? B= Each sheet makes uniform B fields above and below Add up Æ Uniform B field only between the sheets 2 This looks similar to a capacitor Charged sheet makes E fields above and below Two oppositely-charged sheets make uniform E field between µ0 I s Infinite current sheet is less practical to make… B=0 B = µ0 I s B=0 Solenoid Bend the infinite current sheet into a tube Current flows around the tube Uniform B field inside? We can make this by winding a long wire around a cylinder Suppose the winding is dense i.e. large N n= A Turns of winding Solenoid length Also suppose the solenoid is very long Use Ampère’s Law to find out B Solenoid Field B field is parallel to the solenoid’s axis Also, if you go far away, B Æ 0 Apply Ampère to the rectangular path B=0 v∫ B ⋅ ds = BA = µ InA 0 B = µ0 nI Line integral doesn’t change as long as the top and bottom sides of the rectangle remain outside and inside Æ B field is uniform B A Magnetic Flux We can define magnetic flux just like the electric flux Φ B = ∫ B ⋅ dA Φ E = ∫ E ⋅ dA Integral is taken over a given surface area “How many magnetic field lines go through this area?” Units are T·m2 = N·m/A for magnetic flux V·m for electric flux Main use of the electric flux was Gauss’s Law What happens to it with magnetic field? Gauss’s Law With electric flux, we had Φ E = v∫ E ⋅ dA = qin ε0 But there is no magnetic “charge” Gauss’s Law in magnetism: Φ B = v∫ B ⋅ dA = 0 i.e., magnetic flux through any closed surface is zero Not as useful (in solving problems) as the electric version But we’ve got Ampère’s Law instead Magnetic flux is a critical ingredient for Faraday’s Law We’ll get to that next week Magnetism in Matter Different materials react differently to magnetic field Read textbook 30.8 Some (e.g. iron) stick and others don’t Things get a bit encylopedic Three types of magnetism Ferromagnetism – strongly attracted to magnets Paramagnetism – weakly attracted to magnets Iron (ferrrum), cobalt, nickel, etc. Ferromagnetic metals turn paramagnetic at high temperature Diamagnetism – weakly repelled by magnets Majority of materials Special case: superconductors are strongly diamagnetic Summary Applied Biot-Savart law to linear current B = µ0 I 2π r B field rotates around the current µ0 I1 I 2 A Parallel wires attract each other by F = Ampère’s Law 2π a Definition of Ampere v∫ B ⋅ ds = µ I 0 Applies to any boundary that encircle current I Examples: thick wire, infinite current sheet Solenoid field B = µ0 nI v∫ B ⋅ dA = 0 Gauss’s Law Φ B = Ferro-/para-/diamagnetism in matter