* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Genetic Basis for the plasticity of growth and survival in Crassostrea
Survey
Document related concepts
Transcript
Bruno Ernande, NMA Course, Bergen
On the Evolution
of Phenotypic Plasticity
In Spatially Structured Environments
Bruno Ernande
Fisheries Department
IFREMER
Port-en-Bessin, France
Bruno Ernande, NMA Course, Bergen
Definitions
Phenotype z
∎ Phenotypic plasticity
g1
degree of
plasticity
Phenotype = Genotype + Environment
zij = gi + Ej
a single genotype can produce
different phenotypes according to the
environment where it develops and
lives
this holds for both spatial and
temporal environmental variation
∎ Reaction norm
g2
Environment E
the systematic profile of phenotypes zij
expressed by a single genotype gi in
response to a given range of
environments Ej
∎ Phenotypic plasticity may be an active
process allowing short term
adaptation. Can it be selected for?
Bruno Ernande, NMA Course, Bergen
Prerequisites for phenotypic plasticity to evolve
∎ To be selected for, phenotypic plasticity needs to
Ve
Phenotype z
enhance fitness of plastic genotypes relative to non-plastic ones
be under genetic control
exhibit sufficient additive genetic variance in the population
g1
g2
Vp V
g
g1
Ve
Environment E
Vp = Vg + Ve
g2
Environment E
Vp = Vg + VE + VgE
∎ Requirements are met in both plants and animals: Schlichting 1986; Sultan 1987;
Scheiner 1993; Pigliucci 1996
Bruno Ernande, NMA Course, Bergen
How to represent reaction norms in models?
z
z
gi
zi5
zi4
zi3
zi2
zi1
gi
Slope, s
zi0
intercept
1
2
3
4
5 E
∎ Character-state reaction norm
{zi1, zi2, zi3, zi4, zi5}: the different
character-states are evolving under
the constraints imposed by
correlations across environments
Falconer 60’s, Via and Lande 1985,
Kawecki and Stearns 1993
E0
E
∎ Polynomial reaction norm
{zi0 , s}: intercept and slope are
considered as the evolving traits.
Gavrilets and Scheiner 1993a,b
Bruno Ernande, NMA Course, Bergen
How to represent reaction norms in models?
z
gi
zi(E)
E
∎ Reaction norm as a functional trait
zi(E): reaction norm is represented by a flexible function which can evolve like a
trait
Gomulkiewicz & Kirkpatrick 1992
This of course the most flexible way to model a reaction norm
Bruno Ernande, NMA Course, Bergen
Previous models of phenotypic plasticity evolution
∎ Optimality Theory: Ecologically oriented models
Geared toward identifying the selective pressures favouring or preventing the
evolutionary emergence of phenotypic plasticity
― from explicit ecological scenarios and
― a priori trade-offs
Based on population dynamics, no genetics: phenotypic evolution
Long-term evolution but no evolutionary transients, only evolutionary equilibria
No density- nor frequency-dependent populations: interactions between individuals
are not accounted for
Stearns and Koella 1986; Houston and McNamara 1992; Kawecki and Stearns 1993;
Sasaki & de Jong, 1999
Bruno Ernande, NMA Course, Bergen
Previous models of phenotypic plasticity evolution
∎ Quantitative genetics: Genetically oriented models
Aim at identifying the implications of the underlying genetics for the evolutionary
emergence of phenotypic plasticity, focusing mainly on genetic constraints such as
― the lack of additive genetic variance or
― genetic correlations
Based on a statistical description of the population, no detailed ecology
Evolutionary transients together with equilibria, but short term evolution (constant
additive genetic (co-)variance matrix)
No density- nor frequency-dependent populations: interactions between individuals
are not accounted for
Via and Lande 1985, 1987; Van Tienderen 1991, 1997;Gomulkiewicz and Kirkpatrick
1992; Gavrilets and Scheiner 1993
Bruno Ernande, NMA Course, Bergen
Under-investigated aspects
∎ Density-dependent population dynamics and frequency-dependent selection
Would allow to account for phenotypic plasticity triggered by interactions between
individuals such as competition for food resources or mates, predation,…
∎ Accounting for different types of costs of phenotypic plasticity
Maintenance costs: expenses incurred by maintaining the potential for being plastic
Production costs: costs paid by a plastic genotype actually producing a given
phenotype in excess to those incurred by a fixed genotype producing the same
phenotype
∎ The consequence of alternative distribution patterns
Are individuals distributed randomly across environments or do they select it?
∎ The evolutionary implications of a precise environmental setting
Frequency of the different environments, the quality of the resource they offer…
How these factors are driving the potential evolution of phenotypic plasticity,
how do they interact and what is their relative importance?
Bruno Ernande, NMA Course, Bergen
The modelling approach
∎ We use adaptive dynamics theory (Metz et al. 1992; Dieckmann & Law 1996; Metz
et al. 1996; Geritz et al. 1998) and its recent extension to function-valued traits
∎ Properties and assumptions:
Selection gradient derived from explicit ecological scenarios
Phenotypic model (clonal model), no genetics
Long term evolution of phenotypic plasticity: mutation driven (slow mutation rate,
small mutational steps)
Describes adaptive transient states together with evolutionary equilibria
Allows to account for interactions between individuals
― density-dependent population dynamics and
― frequency-dependent selection
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
The basics
∎ Individuals are living across a range of environments e that can represent:
abiotic parameters (temperature, salinity, amount of nitrates…)
biotic characteristics (species or densities of preys, of predators, types of
competitors )
∎ The phenotype p can vary across environmental types e according to a function
p(e) which is a reaction norm
∎ Determinants of environmental heterogeneity:
How frequent are the different environmental types? Frequency of occurence o(e)
What is the quality of the different environments? Intrinsic carrying capacity k(e)
How sensitive to phenotypic variation is the performance of organisms in each type
of environment? Sensitivity to maladaptation s(e)
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
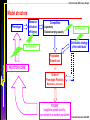
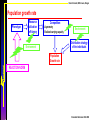
Model structure
Phenotype
Resource
utilization
efficiency
Competition:
-Asymmetry
-Realized carrying capacity
Environment
Distribution strategy
of the individuals
Environment
Population
Growth rate
REACTION NORM
+
Costs of
Phenotypic Plasticity
Maintenance, production
FITNESS
Long term growth rate of a
rare mutant in a resident population
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
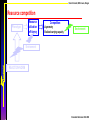
Resource utilization efficiency
Phenotype
Resource
utilization
efficiency
Environment
REACTION NORM
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Resource utilization efficiency
∎ In each environment e, a matching phenotype m(e) maximizes efficiency of
resource utilization Ep(e) (harvesting, handling, digestibility,…)
along an
environmental gradient
Efficiency, Ep(e)
in a given
environment e
1
sensitivity
s(e)
s(e)
0
p(e) m(e)
Phenotype, p(e)
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Resource competition
Phenotype
Resource
utilization
efficiency
Competition:
-Asymmetry
-Realized carrying capacity
Environment
Environment
REACTION NORM
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Resource competition
∎ Competition for resources
logistic density-dependence with a coefficient of competition A(E) and a realized
carrying capacity kp(e), both depending on the resource utilization efficiency.
Competition coefficient, A(E)
2
k(e)
a=0
a<1
E>0
a=1
1
E<0
a>1
degree of
asymmetry
0
0
0
Difference in efficiency, E
0
Efficiency, Ep(e)
1
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
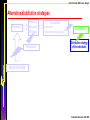
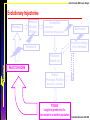
Alternative distribution strategies
Phenotype
Resource
utilization
efficiency
Environment
Competition:
-Asymmetry
-Realized carrying capacity
Environment
Distribution strategy
of the individuals
REACTION NORM
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Alternative distribution strategies
Occurrence, o(e)
Quality, k(e)
Efficiency, Ep(e)
∎ Random Distribution:
No selective control over local habitat
Distribution, dp(e)
Environment, e
Occurrence, o(e)
Quality, k(e)
Efficiency, Ep(e)
Distribution, dp(e)
Occurrence, o(e)
Quality, k(e)
Efficiency, Ep(e)
Distribution, dp(e)
∎ Ideal Free Distribution:
Individuals can detect intrinsic quality of the
different environments
∎ Optimal Foraging:
Individuals can both detect intrinsic quality
of the different environments and distribute
according to their efficiency.
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Population growth rate
Phenotype
Resource
utilization
efficiency
Competition:
-Asymmetry
-Realized carrying capacity
Environment
Distribution strategy
of the individuals
Environment
Population
Growth rate
REACTION NORM
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
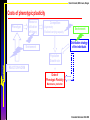
Costs of phenotypic plasticity
Phenotype
Resource
utilization
efficiency
Competition:
-Asymmetry
-Realized carrying capacity
Environment
Distribution strategy
of the individuals
Environment
Population
Growth rate
REACTION NORM
+
Costs of
Phenotypic Plasticity
Maintenance, production
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Costs of phenotypic plasticity
∎ Costs increase with departure from
the developmental base-line.
Phenotype, p(e)
The total costs of the reaction norm
are proportional to its variance
around the developmental base-line.
Environment, e
Distribution, dp(e)
Maintenance
Production
∎ Three types of costs
maintenance costs independent of
the distribution of the individuals
production costs depending fully on
the distribution
mixed cost
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
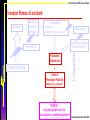
Invasion fitness of a mutant
Phenotype
Resource
utilization
efficiency
Competition:
-Asymmetry
-Realized carrying capacity
Environment
Distribution strategy
of the individuals
Environment
Population
Growth rate
REACTION NORM
+
Costs of
Phenotypic Plasticity
Maintenance, production
FITNESS
Long term growth rate of a
rare mutant in a resident population
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Canonical equation
∎ Fitness of a rare mutant p’ in a resident population p:
f p, p Growth rate p, p Costs p, p
frequency-dependence
∎ Adaptive dynamics of a function valued trait p are are given by:
d
1
p(e) nˆ p p 2 (e, e) g p (e) de
dt
2
with
Dieckmann & Heino 2001
p(e,e’): the mutational variance-covariance function,
gp(e): the selection gradient in environmental type e is the functional
derivative of the fitness function f(p’,p) at trait p’ = p.
g p e lim
0
f p e , p f p, p
f p e , p
0
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Evolutionary trajectories
Phenotype
Resource
utilization
efficiency
Competition:
-Asymmetry
-Realized carrying capacity
Environment
Distribution strategy
of the individuals
Environment
Population
Growth rate
REACTION NORM
+
Costs of
Phenotypic Plasticity
Maintenance, production
FITNESS
Long term growth rate of a
rare mutant in a resident population
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Evolutionary equilibria
∎ Evolutionary equilibria p* or evolutionary singularities are attained when:
p*
2
(e, e) g p* (e) de 0
∎ This is possible when
the selection gradient vanishes at p*, gp*(e’) = 0
Selection induced-equilibria.
the mutational variance-covariance function p*2(e,e’) is singular at p*
Covariance induced equilibria.
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Selection-induced equilibria
∎ Evolutionary singularities are characterized by a balance between two opposing
forces:
one toward the matching phenotype m(e) with a weight m
the other toward the cost-free generalist phenotype p with a weight g
p * (e) [m (e)m(e) g (e) p*] /[m (e) g (e)]
∎ The weights of the two forces depend on the distribution strategy of the
individuals:
R.D.
m (e) (1 2a)r wx w(e)s(e)
g (e) c w / KE p* wx (e) K (e)
I.F.D.
m (e) (1 2a)r wx K x w(e) K (e) s(e)
g (e) c wK / E p* wx (e) K x (e)
O.F.
m (e) (1 2a)r wx K x E px* w(e) K (e) s(e)
g (e) c wKE p* wx (e) K x (e)
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Evolutionary effect of the different types of costs
∎ As costs are shifting from
maintenance to production type (i.e.
increases), the effects of:
p
the frequency of occurence o(e) of
the different environmental types in
case of all distribution strategies,
the intrinsic carrying capacity k(e) in
case of Ideal Free Distribution and
Optimal Foraging.
∎ on the shape of the reaction norm
disappear.
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Evolutionary effect of the distribution strategies
∎ The effect of carrying capacity differs
according to the kind of distribution
strategy considered:
p
in case of Random Distribution,
better matching evolve in poor
environments
in of Ideal Free Distribution and
Optimal Foraging, better matching
evolves in good environmental types
Ernande & Dieckmann 2004 JEB
Bruno Ernande, NMA Course, Bergen
Evolutionary branching of reaction norms
∎ If costs of plasticity and sensitivity
are higher
1. Directional selection
monomorphic maladapted reaction
norm
2. Selection turns disruptive
evolutionarily non-stable
Monomorphic
Dimorphic1
Dimorphic 2
3. Protected dimorphism in reaction
norm:
Evolution of Trophic Specialization.
Bruno Ernande, NMA Course, Bergen
Conclusions
∎ Evolution of phenotypic plasticity can be driven by frequency-dependent
interaction between conspecifics allow for branching of reaction norms and
apparition of polymorphism in the degree of phenotypic plasticity.
∎ Considering different type of costs of phenotypic plasticity have a drastic effect
on the shape of reaction norm: interact in an intricate manner with the
environmenal setting;
∎ Distribution strategy of the individuals is a crucial factor: changes the effect of
the quality of the environments and the susceptibility for branching in reaction
norms
∎ Promising developments:
the systematic exploration of branching points in reaction norms,
the evolutionary competition between generalist, specialist and “plasticist”: the
coevolution between distribution patterns and phenotypic plasticity,
development of a model in case of a temporally fluctuating environment.