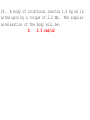Download Lecture23 - Purdue Physics

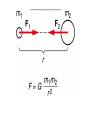
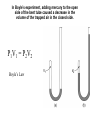
Fig. 5.4
Centripetal Acceleration:
a = v2/r
Directed inwards, towards the center.
A lever is used to lift a rock. A small force F1
generates a larger force F2 to lift the rock, but
F1 acts through a larger distance d1 than does F2.
In other words, the work you do equals the work done on
the rock. (Conservation of energy.)
A crate is moved a distance d across a concrete floor
under the influence of a constant horizontal force F.
WORK = Force times Distance
Can work be negative?
The work done on an object by the net force acting on the
object results in an increase in the object’s kinetic energy.
What about friction?
Important concepts
1. Work = force x distance
2. Kinetic energy KE = (1/2)mv2
3. Total work done = change in KE
4. Potential energy from gravity PE = mgh
5. Energy is conserved:
E = KE + PE = constant! (Some restrictions apply!!)
Conservation of mechanical energy:
If there are no forces doing work on a system, the total
mechanical energy of the system remains constant.
If W=0,
E = PE + KE = constant.
Momentum is a vector:
Magnitude = mass times speed = mv
Direction = same as velocity
(To be more precise, this is the linear momentum.)
If the net external force acting on a system of
objects is zero, the total momentum of the
system is conserved.
We also want to know about changes in momentum.
Notation:
initial momentum pi
final momentum
change in momentum
pf
Dp = pf - pi
There is a close resemblance between quantities
used to describe linear motion and those
used to describe rotational motion.
Figure 8.15
Expressions for the rotational inertia of
several objects, each with a uniform distribution
of mass over its volume. The letter m is used to
represent the total mass of the object.
Physics of Angular Motion
1. If the total torque on an object is zero, then
it does not rotate, or it rotates at a constant
angular velocity.
Physics of Angular Motion
2. The net torque on an object is proportional
to its angular acceleration. The constant of
proportionality is the moment of inertia.

(vectors)
Physics of Angular Motion
3. If the net torque on a system is zero, the
total angular momentum of the system is
conserved.
L=I
(vectors)
CONCEPT
Linear Motion
Rotational
Inertia
m
I
Second Law
F=ma

Momentum
P=mv
L=I
conservation
P=constant,
if F=0.
KE=1/2mv2
L=constant,
if 
KE=1/22
Kinetic energy
A woman’s high heels sink into the soft ground,
but the larger shoes of the much bigger man do not.
Pressure = force/area
Pascal’s Principle:
Any change in the pressure of a fluid is
transmitted uniformly in all directions
throughout the fluid.
In Boyle’s experiment, adding mercury to the open
side of the bent tube caused a decrease in the
volume of the trapped air in the closed side.
P1V1 = P2V2
Boyle’s Law
Archimedes’ Principle:
The buoyant force acting on an
object fully or partially submerged
in a fluid is equal to the weight of
the fluid displaced by the object.
What is heat?
It is the energy that flows from a hot
object to a cooler one.
Will adding heat to a body always
raise its temperature?
No, there can be a change of phase.
It takes 0.49 cal to raise 1 gram of ice
from -1 C to 0 C.
But, it takes another 80 cal to go from ice
at 0 C to water at 0 C.
Similarly, it takes 540 cal to go from 1
gram of water at 100 C to one gram of
steam at 100 C.
An object can get hotter by
• adding heat to it
• doing work on it!
Total energy is conserved. Heat is another form of energy.
1.
When an ice skater twirling on the
point of a skate draws her arms in she
ends up whirling faster. This is because -A.
B.
C.
D.
rotational energy is conserved.
angular momentum is conserved.
linear momentum is conserved.
a net torque acts on the skater.
1.
When an ice skater twirling on the
point of a skate draws her arms in she
ends up whirling faster. This is because -B.
angular momentum is conserved.
2.
Suppose water is boiled in a vessel
open to the atmosphere. Compare the internal
energy of 1 gram of steam at the boiling point to
the internal energy of 1 gram of water at the
same temperature.
A.
The internal energy of the water and steam
are the same.
B.
The internal energy of the water will be
higher.
C.
The internal energy of the steam will be
higher.
2.
Suppose water is boiled in a vessel
open to the atmosphere. Compare the internal
energy of 1 gram of steam at the boiling point to
the internal energy of 1 gram of water at the
same temperature.
C.
The internal energy of the steam will be
higher.
3.
A bullet is fired into a wall and comes to
rest. Considering the bullet as the system we can
say that -A.
the total mechanical energy is
conserved.
B.
the momentum is conserved.
C.
both total mechanical energy and
momentum are conserved.
D.
neither total mechanical energy nor
momentum are conserved.
3.
A bullet is fired into a wall and comes to
rest. Considering the bullet as the system we can
say that -D.
neither total mechanical energy nor
momentum are conserved.
4.
Anthea exerts a force of 500 N against a
100-kg desk which does not move. Campaspe
exerts a force of 400 N against a 60-kg desk
which moves 2 m in the direction of the push.
Fiorinda exerts a force of 200 N against a 50kg desk which moves 4 m in the direction of the
push. The most work is done by
A.
Anthea.
B.
Campaspe.
C.
Fiorinda.
D.
Campaspe and Fiorinda, who do equal
amounts of work.
4.
Anthea exerts a force of 500 N against a
100-kg desk which does not move. Campaspe
exerts a force of 400 N against a 60-kg desk
which moves 2 m in the direction of the push.
Fiorinda exerts a force of 200 N against a 50kg desk which moves 4 m in the direction of the
push. The most work is done by
D.
Campaspe and Fiorinda, who do equal
amounts of work.
5.
free
with
of 5
A truck of mass 4000 kg is at rest but
to roll with no resistance. If you push
a force of 500 N, the momentum at the end
s of pushing will be
A.
zero.
B.
500 N.
C.
800 kg/s.
D.
2500 kg m/s.
5.
free
with
of 5
A truck of mass 4000 kg is at rest but
to roll with no resistance. If you push
a force of 500 N, the momentum at the end
s of pushing will be
D.
2500 kg m/s.
6.
A merry-go-round is set in motion by
students applying a a force of 500 N
tangential to the rim of the wheel having a
radius of 2.0 m. The merry-go round reaches a
rotational velocity of 2.0 rad/s after 10
seconds, starting from rest. The rotational
inertia of the merry-go-round is
A.
1.0 x 105 kg m2
B.
5.0 x 103 kg m2
C.
5.0 x 104 kg m2
D.
5.0 x 105 kg m2
E.
1.0 x 104 kg m2
6.
A merry-go-round is set in motion by
students applying a a force of 500 N
tangential to the rim of the wheel having a
radius of 2.0 m. The merry-go round reaches a
rotational velocity of 2.0 rad/s after 10
seconds, starting from rest. The rotational
inertia of the merry-go-round is
B.
5.0 x 103 kg m2
7.
A hard rubber ball is thrown against a
wall and rebounds with nearly the same speed
that it had initially. A tomato of the same
mass is thrown against the wall with the same
speed, splatters and hardly rebounds. The
impulse exerted by the wall on each object-A.
is larger for the tomato
B.
is the same for both and not zero
C.
is zero for both
D.
is larger for the ball.
7.
A hard rubber ball is thrown against a
wall and rebounds with nearly the same speed
that it had initially. A tomato of the same
mass is thrown against the wall with the same
speed, splatters and hardly rebounds. The
impulse exerted by the wall on each object-D.
is larger for the ball.
8.
In using a long steel rod as a lever to move
a large rock, where should the fulcrum be placed?
A.
B.
C.
D.
Halfway between the rock and the applied
force.
Close to the rock.
Close the point where the force is applied.
Anywhere in between -- it makes no
difference.
8.
In using a long steel rod as a lever to move
a large rock, where should the fulcrum be placed?
B.
Close to the rock.
9.
A ball at the end of a string is started
swinging as a simple pendulum. Assuming no
loss in energy due to friction we can say for
the ball that
A.
the potential energy is maximum at
the center of motion.
B.
the potential energy is maximum
where the kinetic energy is a
minimum.
C.
the potential energy is maximum
where the kinetic energy is maximum.
D.
the kinetic energy is maximum at
each end of the motion.
9.
A ball at the end of a string is started
swinging as a simple pendulum. Assuming no
loss in energy due to friction we can say for
the ball that
B.
the potential energy is maximum
where the kinetic energy is a
minimum.
10. A penny, a quarter and a silver dollar lie
at the bottom of a wishing well filled with
water. The coin experiencing the largest
downward force due to the water pressure is:
A.
penny
B.
quarter
C.
silver dollar
D.
all the same
10. A penny, a quarter and a silver dollar lie
at the bottom of a wishing well filled with
water. The coin experiencing the largest
downward force due to the water pressure is:
C.
silver dollar
11. An ice cube of mass 100 g and at 0 C is
dropped into a styrofoam cup containing 200 g
of water at 25 C. The heat of fusion of ice
is 80 cal/g and the specific heat capacity of
water is 1.0 cal/g C. Assuming the cup
doesn't exchange any heat, the final
temperature of the system will be which of the
following?
A.
-10 C
B.
0 C
C.
+10 C
D.
+2.5 C
E.
+5.0 C
11. An ice cube of mass 100 g and at 0 C is
dropped into a styrofoam cup containing 200 g
of water at 25 C. The heat of fusion of ice
is 80 cal/g and the specific heat capacity of
water is 1.0 cal/g C. Assuming the cup
doesn't exchange any heat, the final
temperature of the system will be which of the
following?
B.
0 C
12. A piece of aluminum has a mass of 0.25 kg
and a density of 2700 kg/m3. The buoyant
force exerted on this body when completely
submerged in water of density 1000 kg/m3 is
approximately:
A.
2.4 N
B.
1.2 N
C.
0.91 N
D.
0.093 N
E.
2.45 x 10-3 N
12. A piece of aluminum has a mass of 0.25 kg
and a density of 2700 kg/m3. The buoyant
force exerted on this body when completely
submerged in water of density 1000 kg/m3 is
approximately:
C.
0.91 N
13. A painter of mass 80 kg climbs 3.0 m up a
ladder. The painter has gained potential
energy in amount of -A.
240 J
B.
784 J
C.
2352 J
D.
261 J
E.
1284 J
13. A painter of mass 80 kg climbs 3.0 m up a
ladder. The painter has gained potential
energy in amount of -C.
2352 J
14. A body of rotational inertia 1.0 kg m2 is
acted upon by a torque of 2.0 Nm. The angular
acceleration of the body will be:
A.
0.50 rad/s2
B.
0.5 rev/s2
C.
1.0 rad/s2
D.
2.0 rad/s2
E.
2.0 rev/s2
14. A body of rotational inertia 1.0 kg m2 is
acted upon by a torque of 2.0 Nm. The angular
acceleration of the body will be:
D.
2.0 rad/s2
15. A box is moved 10 m across by a floor a
force of 20 N acting along the direction of
motion. The work done is
A.
2.0 J
B.
20 J
C.
30 J
D.
100 J
E.
200 J
15. A box is moved 10 m across by a floor a
force of 20 N acting along the direction of
motion. The work done is
E.
200 J
16. An object of mass 1.0 kg with a velocity
of 4.0 m/s strikes head-on a second object of
mass 2.0 kg at rest. After the collision the
first body moves backward at 1.0 m/s and the
struck body moves forward with a velocity of
2.5 m/s. In this collision -A.
momentum is conserved but kinetic energy
is not
B.
kinetic energy is conserved but momentum
is not
C.
momentum and kinetic energy are conserved
D.
neither momentum nor kinetic energy are
conserved.
16. An object of mass 1.0 kg with a velocity
of 4.0 m/s strikes head-on a second object of
mass 2.0 kg at rest. After the collision the
first body moves backward at 1.0 m/s and the
struck body moves forward with a velocity of
2.5 m/s. In this collision -A.
momentum is conserved but kinetic energy
is not.