* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download MEL 417 Lubrication Minor I
Coandă effect wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Sir George Stokes, 1st Baronet wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Hemodynamics wikipedia , lookup
Boundary layer wikipedia , lookup
Accretion disk wikipedia , lookup
Aerodynamics wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Reynolds number wikipedia , lookup
Hemorheology wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Fluid dynamics wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
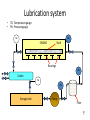
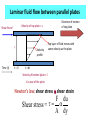
MEL 417 Lubrication Minor I Date: Tuesday, 08/02/2011 Time: 4 – 5 pm. Venue: Bl. V, 419 Extreme Pressure Boundary Lubrication • Active chemicals, such as chlorine, sulfur, and phosphorus form inorganic film of low shear strength (chlorides, sulfides, phosphides). – EP additives react with sliding surfaces under severe conditions in contact zone to give compound with low shear strength, thus forming a lubricating film at precisely a location where it is needed. 2 Boundary vs. EP lubrication • BL is restricted to those systems where there is thermodynamic reversibility. A small change in temperature or concentration, up or down, brought about a related change in film coverage. • If lubricant reacts chemically with metal, then lubrication should properly be considered a type of extreme pressure lubrication, which is considered in next slide. – EP lubricants are inorganic molecules that provide good lubrication at elevated temperature & pressure – Reaction of E.P. additive does not occur rapidly at low temp. 3 Extreme Pressure Lubricants Lubricant containing chlorine forming CuCl or CuCl2 on surface, providing protection against adhesive wear. .. 800C. Iron Chloride649°C Sulfur and phosphorus are common additives for iron and steel. Films have relatively high melting point Iron sulphide- 1,170°C • Major difficulty - carcinogenic nature, environmental pollutant. – Removal of sulfur compound present in small amounts in petroleum based lubricants requires elaborate and expensive refining techniques. 4 Hydrodynamic and sqeeze film lubrication SQUEEZE FILM LUBRICATION HYDRODYNAMIC LUBRICATION Load Load PRESSURE DISTRIBUTION 10-50 mm Relative movement of bearing surfaces Relative movement of bearing surfaces Elastohydrodynamic lubrication RIGID BEARINGS Pressure distribution Load Pressure distribution Load Squeeze film Rolling Thin fluid film, high pressures DEFORMABLE BEARINGS (Elastohydrodynamic) Pressure distribution Load Pressure distribution Load Squeeze film Rolling Larger area, low pressures Weeping lubrication in bone joints When the cartilage tissue on both sides come in contact, fluid is squeezed out into the joint space cartilage cartilage Space filled with a layer of fluid 7 Lubrication Mechanisms hmin • Boundary lubrication, 2 2 <1 Rrms R ,a rms,b • Hydrodynamic • Dimensionless film lubrication, >5 parameter (“Specific film • Mixed lubrication, thickness”) 1<<3 • Elastohydrodynamic, 3<<5 8 Streibeck curve Left of a- boundary lubrication Coefficient of friction m Between a and c- mixed film lubrication Mixed film friction/lubrication Right of c- fluid film lubrication b- Minimum coefficient of friction Fluid film friction/lubrication a b Boundary friction/lubrication c Viscosity velocity Load Lubrication system • • TG- Temperature gauge PG- Pressure gauge PG TG ENGINE Shaft Bearings PG Cooler TG PG Storage tank Pump Filter 10 10 Viscosity Ideal fluid (Pascalian) • Frictionless • Incompressible • Experience only normal force and no drag force • Does not adhere to a solid surface • Relative tangential velocity with surface is known as slip Real fluid • Experience both tangential and normal force during motion • Attaches to a solid boundary in contact (no slip) • There is resistance to flow between molecules of the fluid and is known as “internal friction” • Viscosity is a measure of the internal friction • Also known as viscous fluids Viscosity • The property characterizing internal resistance to fluid flow • Defines the frictional force between layers of the fluid Direction of flow Fluid layers Resistance to flow Solid surface Laminar fluid flow between parallel plates Velocity of top plate = u Shear force F y Time (t) t=0 Velocity profile Direction of motion of top plate Top layer of fluid moves with same velocity as the plate t = dt Velocity of bottom plate = 0 A is area of the plate Newton’s law: shear stress shear strain F du Shear stress = A dy Fluid element subject to shear stress du.dt Velocity = u + du dy Fluid element Velocity = u t=0 d Fluid element t = dt For slow viscous flow, tan(d) ~ d du.dt tan( d) dy or strain rate d du dt dy Newton’s hypothesis of viscosity • Shear force is proportional to area • Shear force is proportional to velocity • Shear force is inversely proportional to film thickness Therefore shear force F • A is the surface area of fluid layer • du is the velocity • dy is the film thickness A.du dy Coefficient of dynamic viscosity • Therefore Shear stress = or F du A dy du h dy h is the coefficient of dynamic viscosity or absolute viscosity Coeff. of dynamic viscosity (units) F dy h . A du In F.P.S system In C.G.S system In S.I. units lb . sec h reyn 2 in . (Named after Reynolds) dyne . sec h poise 2 cm. (Named after Poiseuille) h pressure . sec . pascal. sec pa.s Coefficient of kinematic viscosity • The ratio of absolute viscosity to density Coefficient of kinematic viscosity h Used when flow of fluid is influenced by gravity (as density influences weight) The units in C.G.S is the stoke or centistoke (1/100 stokes) Effect of temperature on viscosity • Viscosity decreases with rise in temperature • Amount of decrease depends upon source of oil, refining and blending procedures and the presence of additives • Temperature-viscosity relationship is important as viscosity determines the load bearing capacity • Walther’s formula: log (+C) = A/Rm A and m are constants, R is the temperature in degree Rankine, C ranges from 0.6 to 0.8 ASTM (American Society for Testing Materials) viscosity equation Log.[log( + C)] = log(A) – m.log(T) A and m are constants is the kinematic viscosity T is the temperature in Kelvin C is a function of ASTM chart for viscosity Log[log( + C)] P1 P1 and P2 obtained from experiment, P obtained from chart P P1 T1 T2 Log T Viscosity index (number indicating change in viscosity with temperature) L- viscosity of low-grade oil at 40 oC (Dean and L Davis method) V- viscosity of test, low grade, and high grade oils at 100 oC (same and known) Viscosity VI is basically calculated using a scale of 0 to 100. The value can come to above 100 H- viscosity of high-grade oil at 40 oC U- viscosity of test oil at 40 oC U H V High grade: Less viscosity change with temperature change Low grade: More viscosity change with temperature change 40 oC Temperature T 100 oC Viscosity index calculation L U L-U V V .100 .100 Viscosity index (VI) = L H L-H V V L is the viscosity of low grade oil H is the viscosity of high grade oil U is the viscosity of test oil VI of high grade oil is taken as 100 VI of low grade oil is taken as 0 Therefore above formula gives VI of the test oil on a scale of 0 to 100 Viscosity index calculation (contd.) • If the viscosity is lower than H at 40 oC, the VI > 100 • In such cases, the ASTM equation for viscosity calculation is 10 - 1 VI 100 0.00715 N log H - log U N log U Pressure effect on viscosity • Viscosity increases with pressure as h h0 e p ho is the dynamic viscosity at atmospheric pressure (Ns/m2) h is the dynamic viscosity at pressure p (Ns/m2) is the pressure viscosity coefficient (m2/N) Newtonian fluid • Fluids obeying Newton’s law of viscous flow • Viscosity is independent of shear rate and shear stress • Shear strain under action of shear stress linearly increases with time • Strain is not recovered when the shear stress is withdrawn • Linear stress-shear relationship is for a particular temperature and pressure under laminar flow Shear rate Newtonian fluid: shear stress-shear strain relationship du h dy du dy •Linear dependence •Slope is 1/h Shear stress Non-Newtonian Fluids • Do not behave like Newtonian fluids • E.g. Slurries, greases, jams, toothpaste • Deformation and flow behavior varies Bingham plastics Shear rate • Do not flow unless shear stress exceeds a minimum value • Behave like Newtonian fluids beyond this value • E.g. lubricating greases, pastes, waxy crude du dy o Shear stress Bingham plastics (contd.) • Below a shear stress value (shown o) it behaves like an elastic solid (deformation is finite and disappears when shear stress is withdrawn) • Below this value of shear stress, it behaves as Newtonian • If shear stress is withdrawn, the deformation is reduced showing partly plastic behavior u h 0 y u 0 y If > 0 If < 0 Pseudoplastic fluids • E.g. dripless paint, paper pulp, cutting oils, polymeric solutions • Viscosity decreases with increase in shear rate • Due to shear thinning (orientation and formation of polymeric molecules) • Due to rupture of ingredients Shear rate Pseudoplastic: Shear stress-shear rate curve du dy Shear stress Governing equation: (A, B, are constants, B < 1) u A y B-1 u . y Dilatant fluids Governing equation same as for pseudoplastics (A, B, are constants, B > 1) Shear rate • E.g. pastes, inks, butter • Increase in viscosity with rate of shear (shear thickening) du dy u A y Shear stress B-1 u . y Boltzmann (thixotropic) fluids • Time dependent behavior • E.g. heavy oils, asphalts, greases, ice cream, chocolates • Decrease in viscosity over time under the action of a constant shear stress • When shearing is stopped, the thixotropic substance may recover its viscosity with time Boltzman fluids Viscosity (h) recovery du dy constant du dy Time (t) removed