* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Operations with Complex Numbers
Bra–ket notation wikipedia , lookup
Eisenstein's criterion wikipedia , lookup
History of algebra wikipedia , lookup
Cubic function wikipedia , lookup
Elementary algebra wikipedia , lookup
Quadratic form wikipedia , lookup
System of polynomial equations wikipedia , lookup
Factorization wikipedia , lookup
Quadratic equation wikipedia , lookup
Real number wikipedia , lookup
Exponentiation wikipedia , lookup
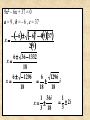
Complex Numbers, p. 126-130 (1.5) OBJECTIVES •Use the imaginary unit i to write complex numbers •Add, subtract, and multiply complex numbers •Use quadratic formula to find complex solutions of quadratic equations Consider the quadratic equation x2 + 1 = 0. What is the discriminant ? a = 1 , b = 0 , c = 1 therefore the discriminant is 02 – 4 (1)(1) = – 4 If the discriminant is negative, then the quadratic equation has no real solution. (p. 114) Solving for x , gives x2 = – 1 x 1 2 x 1 We make the following definition: i 1 Note that squaring both sides yields i 2 1 Real numbers and imaginary numbers are subsets of the set of complex numbers. Real Numbers Imaginary Numbers Complex Numbers Definition of a Complex Number p. 126 If a and b are real numbers, the number a + bi is a complex number written in standard form. If b = 0, the number a + bi = a is a real number. If b 0, the number a + bi is called an imaginary number. A number of the form bi, where b 0 , is called a pure imaginary number. Write the complex number in standard form 1 8 1 i 8 1 i 4 2 1 2i 2 Try p. 131 # 5-16 Equality of Complex Numbers p. 126 Two complex numbers a + bi and c + di, are equal to each other if and only if a = c and b = d a bi c di Find real numbers a and b such that the equation ( a + 6 ) + 2bi = 6 –5i . a+6=6 2b = – 5 a=0 b = –5/2 p. 131 # 1-4 Addition and Subtraction of Complex Numbers, p. 127 If a + bi and c +di are two complex numbers written in standard form, their sum and difference are defined as follows. Sum: (a bi) (c di) (a c) (b d )i Difference: (a bi ) (c di ) (a c) (b d )i Perform the subtraction and write the answer in standard form. #20 ( 3 + 2i ) – ( 6 + 13i ) 3 + 2i – 6 – 13i –3 – 11i #22 8 18 4 3i 2 8 i 9 2 4 3i 2 8 3i 2 4 3i 2 4 Try p. 131 # 17-26 Properties for Complex Numbers p.126 Associative Properties of Addition and Multiplication Commutative Properties of Addition and Multiplication Distributive Property of Multiplication Multiplying complex numbers is similar to multiplying polynomials and combining like terms. #28 Perform the operation and write the result in standard form. ( 6 – 2i )( 2 – 3i ) F O I L 12 – 18i – 4i + 6i2 12 – 22i + 6 ( -1 ) 6 – 22i Consider ( 3 + 2i )( 3 – 2i ) 9 – 6i + 6i – 4i2 9 – 4( -1 ) 9+4 13 This is a real number. The product of two complex numbers can be a real number. Complex Conjugates and Division p. 129 Complex conjugates-a pair of complex numbers of the form a + bi and a – bi where a and b are real numbers. ( a + bi )( a – bi ) a 2 – abi + abi – b 2 i 2 a 2 – b 2( -1 ) a2+b2 The product of a complex conjugate pair is a positive real number. To find the quotient of two complex numbers multiply the numerator and denominator by the conjugate of the denominator. a bi c di a bi c di c di c di ac adi bci bdi 2 2 c d 2 ac bd bc ad i 2 2 c d p. 131 # 50 Perform the operation and write the result in standard form. (Try p.131 #45-54) 6 7i 1 2i 6 7i 1 2i 1 2i 1 2i 6 14 5i 6 12i 7i 14i 2 2 1 4 1 2 2 20 5i 5 20 5i 5 5 4 i Principle Square Root of a Negative Number, p. 130 If a is a positive number, the principle square root of the negative number –a is defined as a ai i a . p.128 #66 Use the Quadratic Formula to solve the quadratic equation. 9x2 – 6x + 37 = 0 a = 9 , b = - 6 , c = 37 What is the discriminant? ( - 6 ) 2 – 4 ( 9 )( 37 ) 36 – 1332 -1296 Therefore, the equation has no real solution. 9x2 – 6x + 37 = 0 a = 9 , b = - 6 , c = 37 x 6 6 4937 29 2 6 36 1332 x 18 6 1296 6 1296 x i 18 18 18 1 36i x 3 18 1 2i 3 HOMEWORK Work: p. 131-132 # 1-54, 1-82, 93-103 alt. odd Read p. 189-196 (2.2) PRE QUIZ (2.2) Office hours: MWF 9:00-10:15 or by appointment. Tutoring Walker 206: M-Th 4:30-6:30 pm