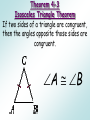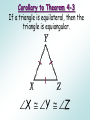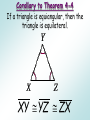* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 4 Lesson 5
History of geometry wikipedia , lookup
Golden ratio wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Euler angles wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Noether's theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Four color theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
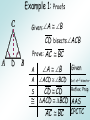
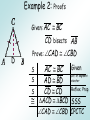
Chapter 4 Lesson 5 Objective: To use and apply properties of isosceles triangles. The congruent sides of an isosceles triangle are its legs. The third side is the base. The two congruent sides form the vertex angle. The other two angles are the base angles. Theorem 4-3 Isosceles Triangle Theorem If two sides of a triangle are congruent, then the angles opposite those sides are congruent. A B Theorem 4-4 Converse of Isosceles Triangle Theorem If two angles of a triangle are congruent, then the sides opposite the angles are congruent. AC BC Theorem 4-5 The bisector of the vertex angle of an isosceles triangle is the perpendicular bisector of the base. CD AB and CD bisects AB . Example 1: Proofs Given: A B CD bisects ACB D Prove: A A S AC BC A B Given ACD BCD Def. of bisector CD CD Reflex. Prop. ACD BCD AAS AC BC CPCTC Example 2: Proofs Given: AC D BC CD bisects AB Prove: CAD CBD S S S AC BC AD BD CD CD Given Def. of segment bisector Reflex. Prop. ACD BCD SSS CAD CBD CPCTC Example 3: Using Algebra Find the values of x and y. By Theorem 4-5, you know thatMO LN, so x = 90. ∆M L N is isosceles, so L N and mN 63. Corollary to Theorem 4-3 If a triangle is equilateral, then the triangle is equiangular. X Y Z Corollary to Theorem 4-4 If a triangle is equiangular, then the triangle is equilateral. XY YZ ZX Assignment Pg. 213 #1-2;7-16; 21-24