Download Chapter 7

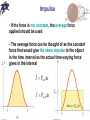
Chapter 7
Impulse and Momentum
Linear momentum
• Linear momentum (or, simply momentum)
point-like object (particle) is

p
of a


p  mv
• SI unit of linear momentum is kg*m/s
• Momentum is a vector, its direction coincides with
the direction of velocity
Newton’s Second Law revisited
• Originally, Newton formulated his Second Law in a
more general form


p
Fnet  lim
t 0 t
• The rate of change of the momentum of an object is
equal to the net force acting on the object
• For a constant mass




p

 (mv )
v
Fnet  lim

lim

m
lim

m
a
t 0 t
t  0
t 0 t
t
Linear momentum for a system of
particles
• We define a total momentum of a system as:



P   pi   mi vi
i
i
• The system includes all the objects interacting with
each other
• Can be generalized to any number of objects
Conservation of linear momentum
• From the Newton’s Second Law


P
Fnet  lim
t 0 t
• If the net force acting on a system is zero, then

P
lim
0
t 0 t

P  const
• If no net external force acts on a system of particles,
the total linear momentum of the system is conserved
(constant)
• This rule applies independently to all components
Fnet , x  0  Px  const
Chapter 7
Problem 25
By accident, a large plate is dropped and breaks into three pieces. The pieces
fly apart parallel to the floor. As the plate falls, its momentum has only a
vertical component and no component parallel to the floor. After the collision,
the component of the total momentum parallel to the floor must remain zero,
since the net external force acting on the plate has no component parallel to
the floor. Using the data shown in the drawing, find the masses of pieces 1 and
2.
Impulse
• During a collision, an object is acted upon by a
force exerted on it by other objects participating in

the collision

Fnet
p
 lim
t 0 t
• For a constant force:



p p
Fnet  lim

t 0 t
t
•We define impulse as:
 
p  Fnet t
 
I  Fnet t
• Then (momentum-impulse theorem)

 
p f  pi  I
Impulse
• If the force is not constant, the average force
applied should be used
• The average force can be thought of as the constant
force that would give the same impulse to the object
in the time interval as the actual time-varying force
gives in the interval
 
I  Fnet t
 
I  Favg t
Impulse
• In the most general case, the impulse imparted by a
force during the time interval Δt is equal to the area
under the force-time graph from the beginning to the
end of the time interval
 
I  Fnet t
 
I  Favg t
Chapter 7
Problem 12
A golf ball strikes a hard, smooth floor at an angle of 30.0° and rebounds at the
same angle. The mass of the ball is 0.047 kg, and its speed is 45 m/s just before
and after striking the floor. What is the magnitude of the impulse applied to the
golf ball by the floor?
Collisions
• A collision is the result of physical contact between
two objects
• Momentum in an isolated system in which a collision
occurs is conserved
• An isolated system will have no external forces and
only internal forces are acting during the collision
• During a collision, the total linear momentum is always
conserved if the system is isolated (no external force)
Elastic and inelastic collisions
• It may not necessarily apply to the total kinetic energy
• If the total kinetic energy is conserved during the
collision, then such a collision is called elastic
• If the total kinetic energy is not conserved during the
collision, then such a collision is called inelastic
• If the total kinetic energy loss during the collision is a
maximum (the objects stick together), then such a
collision is called perfectly inelastic
Elastic collision in 1D
P  const
K  const
2
2
m1v12i m2 v22i m1v1 f m2 v2 f



2
2
2
2
m1v1i  m2 v2i  m1v1 f  m2v2 f
m1 (v1i  v1 f )(v1i  v1 f ) 
m1 (v1i  v1 f )  m2 (v2i  v2 f )
 m2 (v2i  v2 f )(v2i  v2 f )
(m1  m2 )
2m2
v1 f 
v1i 
v2 i
(m1  m2 )
(m1  m2 )
v2 f
2m1
(m2  m1 )

v1i 
v2 i
(m1  m2 )
(m1  m2 )
Elastic collision in 1D: stationary target
(m1  m2 )
2m2
v1 f 
v1i 
v2 i
(m1  m2 )
(m1  m2 )
2m1
(m2  m1 )
v2 f 
v1i 
v2 i
(m1  m2 )
(m1  m2 )
• Stationary target: v2i = 0
• Then
(m1  m2 )
v1 f 
v1i
(m1  m2 )
2m1
v2 f 
v1i
(m1  m2 )
Perfectly inelastic collision in 1D
P  const
m1v1i  m2 v2i  (m1  m2 )v f
m1v1i  m2 v2i
vf 
m1  m2
Chapter 7
Problem 38
A ball is attached to one end of a wire, the other end being fastened to the
ceiling. The wire is held horizontal, and the ball is released from rest (see the
drawing). It swings downward and strikes a block initially at rest on a
horizontal frictionless surface. Air resistance is negligible, and the collision is
elastic. The masses of the ball and block are, respectively, 1.60 kg and 2.40 kg,
and the length of the wire is 1.20 m. Find the velocity (magnitude and direction)
of the ball (a) just before the collision, and (b) just after the collision.
Collisions in 2D

P  const
Px  const
Py  const
Questions?