Download SHM - MACscience

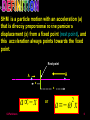
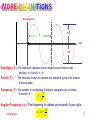
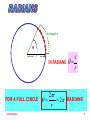
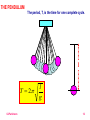
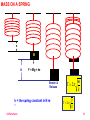
©JParkinson
1
©JParkinson
2
©JParkinson
3
ALL INVOLVE
SIMPLE HARMONIC MOTION
©JParkinson
4
A body will undergo SIMPLE HARMONIC MOTION when the
force that tries to restore the object to its REST POSITION is
PROPORTIONAL TO the DISPLACEMENT of the object.
A pendulum and a mass on a spring both undergo this type of
motion which can be described by a SINE WAVE or a COSINE
WAVE depending upon the start position.
Displacement x
+A
Time t
-A
x  A cos 2ft
©JParkinson
5
SHM is a particle motion with an acceleration (a)
that is directly proportional to the particle’s
displacement (x) from a fixed point (rest point), and
this acceleration always points towards the fixed
point.
Rest point
A
A
x
x
a x
©JParkinson
or
a   x
2
6
Displacement x
+A
T
time
-A
Amplitude ( A ): The maximum distance that an object moves from its rest
position. x = A and x = - A .
Period ( T ):
The time that it takes to execute one complete cycle of its motion.
Units seconds,
Frequency ( f ): The number or oscillations the object completes per unit time.
Units Hz = s-1 .
f 
1
T
Angular Frequency ( ω ): The frequency in radians per second, 2π per cycle.
©JParkinson
  2f 
2
T
7
Arc length s
θ
r
IN RADIANS
FOR A FULL CIRCLE
©JParkinson
2r

 2
r
s

r
RADIANS
8
a   2 x
EQUATION OF SHM
Acceleration – Displacement graph
y m x
a
Gradient = - ω2
+A
x
-A
MAXIMUM ACCELERATION = ± ω2 A
©JParkinson
= ( 2πf )2 A
9
EQUATION FOR VARIATION OF
VELOCITY WITH DISPLACEMENT
v
+x
x
v   2f
A2  x 2
Maximum velocity, v = ± 2 π f A
Maximum Kinetic Energy, EK = ½ mv2 = ½ m ( 2 π f A )2
©JParkinson
10
Displacement x
x  A cos 2ft
t
Velocity v
Velocity = gradient of displacement- time graph
t
Maximum velocity in the middle
of the motion
v 
x
t
ZERO velocity at the end of the
motion
Acceleration = gradient of velocity - time graph
Acceleration a
a 
t
Maximum acceleration at the
end of the motion – where the
restoring force is greatest!
v
t
ZERO acceleration in the middle
of the motion!
©JParkinson
11
THE PENDULUM
The period, T, is the time for one complete cycle.
l
T  2
©JParkinson
l
g
12
MASS ON A SPRING
e
M
A
F = Mg = ke
Stretch &
Release
k = the spring constant in N m1
©JParkinson
m
T  2
k
T  2
e
g
13
The link below enables you to
look at the factors that influence
the period of a pendulum and
the period of a mass on a spring
http://www.explorelearning.com/index.cfm?method
=cResource.dspView&ResourceID=44
©JParkinson
14
ENERGY IN SHM
PENDULUM
SPRING
M
M
potential
EP
Kinetic
EK
Potential
EP
M
potential
kinetic
potential
If damping is negligible, the total energy will be constant
ETOTAL = Ep + EK
©JParkinson
15
Energy in SHM
velocity v   2f
A2  x 2
Maximum velocity, v = ± 2 π f A
Maximum Kinetic Energy, EK = ½ m ( 2 π f A )2 = 2π2 m f2 A2
Hence TOTAL ENERGY = 2π2 m f2 A2
= MAXIMUM POTENTIAL ENERGY!
For a spring, energy stored = ½ Fx = ½ kx2, [as F=kx]
m
F m
x=A
x=0
MAXIMUM POTENTIAL ENERGY = TOTAL ENERGY = ½ kA2
©JParkinson
16
Energy in SHM
= kinetic
= potential
= TOTAL ENERGY, E
energy
Energy Change with POSITION
-A
Energy Change with TIME
E
+A
0
energy
x
E
N.B. Both the kinetic and the
potential energies reach a
maximum TWICE in on cycle.
time
T/2
©JParkinson
T
17
DAMPING
DISPLACEMENT
INITIAL AMPLITUDE
time
THE AMPLITUDE DECAYS EXPONENTIALLY WITH TIME
©JParkinson
18