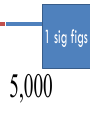Download significant figures

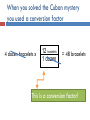
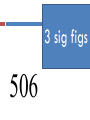
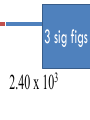
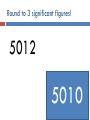
Today’s Do Now 8/11/2014

1) Five different individuals measured the volume of a
sample of sulfuric acid. Their data is in the table to the
right:
Individual Measurement
1
2
3
4
5
2.85
2.87
2.84
2.85
2.86
Today’s Do Now 8/11/2014

Write each of the following numbers in scientific notation:
2. 1,490,000,000
3. 0.00000832

1.49 x 109
8.32 x 10-6
Write the following number in standard notation.
4. 5.36 x 10-2
0.0536
Our first objective…
By the middle of this class period, I will be
able to…
convert between units of measure using
dimensional analysis.
Take a minute…
Mark Cuban has decided that he
wants to leave his position as
general manager and open a
bracelet shop. Before he leaves,
he needs to confiscate 4 dozen
bracelets from his players to start
his shop. How many bracelets
total is Mr. Cuban going to
confiscate?
Dimensional Analysis


Dimensional Analysis: a problem solving
method used to convert between units.
To change from one unit to another we will use
a conversion factor.
Unit1 x conversion factor = Unit2
When you solved the Cuban mystery
you used a conversion factor
4 dozen bracelets x
12 bracelets
1 dozen
= 48 bracelets
This is a conversion factor!
Equivalence statement

Equivalence statement: two
measurements with the exact same
value
Example:
1 dozen = 12
Conversion factor

Conversion factor: ratio of the two parts
of an equivalence statement
Example:
1 dozen = 12
2 Possible conversion factors:
12
OR
1 dozen
1 dozen
12
GaGa for Dimensional Analysis

Example problem: Lady GaGa’s hat
for her meat dress is 10.5 inches
long. What is the length in
centimeters?
Step 1 and 2
1) Identify your given. Circle it in the problem and
write it down.
2) Identify your unknown. Circle it in the problem and
write it down.
Example problem: Lady GaGa’s hat for her
raw meat dress is 10.5 inches long. What is
the length in centimeters?
Step 3
3) Find the equivalence statement(s) that
relates the two units.
1
inch = 2.54 cm
Step 4
4) Choose the correct conversion factor
based upon your given and unknown.

( 1 inch/2.54 cm) OR (2.54cm/1 inch)
Step 5
5) Multiply your given by your
conversion factor; cross off the units
that cancel!
Step 6
6) Round your answer to the correct number of
significant figures
Way to
go!!

The lizard Mr. Pope found was 5.62 cm long. What
was the length of the lizard in inches?
What are the steps?
1.
2.
3.
4.
Identify given and unknown
Find an equivalence statement to relate
the two
The denominator’s units must match the
given.
The numerator’s units must match the
unknown.
Next objective:
By the end of this class period, I will be able
to…
determine the number of significant figures in
an integer to perform calculations reporting the
correct number of significant figures.
UNCERTAINTY IN
MEASUREMENT
Because Nothing in chemistry
is ever certain…
Measuring Volume in the Lab

Volume is measured
from the bottom of
the meniscus
Uncertainty in Measurement
Any measurement involves an
estimate and thus is uncertain
to some extent

Let’s get up and move…
There are 6 graduated cylinders
around the room. Go find at least 2
and take the measurement you think
a scientist would take.
 YOU HAVE 1 MINUTE.

Were you correct?
Number
1
2
3
4
5
6
Volume
Certain vs. Uncertain Numbers


Certain numbers are all of the numbers that can be
said for sure. They will be the same even if 5
different people made a measurement.
Uncertain numbers are any numbers that require an
estimate.
Rules for counting Significant Figures
Rules for counting Significant Figures
1.
Nonzero numbers always count
Ex: 1457 has 4 sig figs
Rules for counting Significant Figures
1.
2.
Nonzero numbers always count
Leading zeros never count
Ex: 0.0025 has 2 sig figs
5 sig figs
15,677
3 sig figs
0.0391
Rules for counting Significant Figures
1.
2.
3.
Nonzero numbers always count
Leading zeros never count
Captive zeros always count
Ex: 1.008 has 4 sig figs
3 sig figs
506
4 sig figs
0.06002
Rules for counting Significant Figures
1.
2.
3.
4.
Nonzero numbers always count
Leading zeros never count
Captive zeros always count
Trailing zeros only count if the number
contains a decimal point
Ex: 100 has only 1 sig fig
100. has 3 sig figs
4 sig figs
0.4700
3 sig figs
2.40 x
3
10
1 sig figs
5,000
Rules for counting Significant Figures
1.
2.
3.
4.
5.
Nonzero numbers always count
Leading zeros never count
Captive zeros always count
Trailing zeros only count if the number
contains a decimal point
Exact numbers (have an unlimited
number)
What is an exact number??

Numbers that are determined by counting:
 10
experiments
 8 molecules

Definitions
1
inch = 2.54 cm
Significant Figures and Rounding

If the digit to be removed:
 A.
is less than 5, the preceding digit stays the
same (1.33 1.3)
 B.
is equal to or greater than 5, the preceding
digit is increased by 1 (1.36  1.4)
Round to 3 significant figures!
0.02345
0.023
5
Round to 3 significant figures!
5012
5010
Round to 3 significant figures!
0.07415
0.074
2
Round to 3 significant figures!
10,001
1.00 x
4
10
Round to 3 significant figures!
567.8
568
Bonus Practice!

Use your number cards to decide
how many significant figures each
number has
1,000.1
5 sig figs
0.004050
4 sig figs
0.000405
3 sig figs
Last Step … back to your notes
Significant Figures in Calculations

For multiplication & division
 The limiting term is the one with the
smallest number of significant figures
4.56 x 1.4 = 6.384
3 sig
figs
2 sig
figs
Round to
6.4
2 sig
figs
Significant Figures in Calculations

Multiplication & Division

Smallest number of significant figures
Work it Out! Swivel Style

Work out the following 4 problems with your lab
partner on the back of your notes sheet:
8.6
0.027
x 0.000556
155
9 x 0.0998 x 286
1.
2.45 x 3.5
2.
8.315 ÷ 298
3.
135 x 246
4.
(3.60 x 10-3) x (8.123) ÷ 4.3
0.0068
Significant Figures in Calculations

For addition & subtraction
 The limiting term is the one with the
smallest number of decimal places
12.161 + 3.12 = 15.281
3 decimal
places
2 decimal
places
Round to
15.28
2 decimal
places
Significant Figures in Calculations

Addition & Subtraction

Smallest number of decimal places
Work it Out! Swivel Style

Work out the following 4 problems with your lab
partner on the back of your notes sheet:
31.1
1.
12.11 + 18.0 + 1.013 =
2.
29.63 + 24.798 + 1.263 =
3.
1081 – 7.25 =
55.69
1074
8.44 x
4. 8.445 x 105 – 9.44 x 102 =
5
10