* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Slide - faculty.ucmerced.edu
Euclidean geometry wikipedia , lookup
Lorentz transformation wikipedia , lookup
Plane of rotation wikipedia , lookup
Line (geometry) wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Rotation matrix wikipedia , lookup
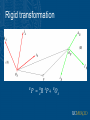
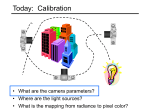
EECS 274 Computer Vision Geometric Camera Models Geometric Camera Models • • • • Elements of Euclidean geometry Intrinsic camera parameters Extrinsic camera parameters General form of perspective projection • Reading: Chapter 1 of FP, Chapter 2 of S Geometric camera calibration Euclidean Geometry Euclidean coordinate system x OP.i x y y OP . j OP x i y j z k P z OP.k z Planes AP n 0 OP n OA n 0 P [ x, y, z ]T , n [a, b, c]T , OA n d ax by cz d 0 Π P 0 where a b Π c d and x y P z 1 homogenous coordinate Pure translation OBP = OBOA + OAP , BP = BOA+ AP AP: point P in frame A Pure rotation 1st column: iA in the basis of (iB, jB, kB) 3rd row: kB in the basis of (iA, jA, kA) i A .i B i .j B R A A B i A .k B j A .i B j A .jB j A .k B k A .i B A i TB k A .jB A jTB k A .k B A k TB B iA B jA B kA Rotation about z axis cos sin B R A 0 sin cos 0 0 0 1 Rotation matrix Elementary rotation R=R x R y R z , described by three angles Properties of rotation matrix • Its inverse is equal to its transpose, R-1=RT , and • Its determinant is equal to 1. Or equivalently: • Its rows (or columns) form a right-handed orthonormal coordinate system. Rotation group and SO(3) • Rotation group: the set of rotation matrices, with matrix product – Closure, associativity, identity, invertibility • SO(3): the rotation group in Euclidean space R3 whose determinant is 1 – Preserve length of vectors – Preserve angles between two vectors – Preserve orientation of space Pure rotations OP i A jA P R P B B A A A x A k A y i B Az jB B x B k B y Bz Rigid transformation B P R P OA B A A B Block matrix manipulation A11 A A21 A12 A22 B11 B B21 B12 B22 What is AB ? A11B11 A12 B21 AB A21B11 A22 B21 A11B12 A12 B22 A21B12 A22 B22 Homogeneous Representation of Rigid Transformations B P AB R T 1 0 B O A A P AB R AP BO A B A P AT 1 1 1 1 Rigid transformations as mappings Rotation about the k Axis Affine transformation • Images are subject to geometric distortion introduced by perspective projection • Alter the apparent dimensions of the scene geometry Affine transformation • In Euclidean space, preserve – Collinearity relation between points • 3 points lie on a line continue to be collinear – Ratio of distance along a line • |p2-p1|/|p3-p2| is preserved Shear matrix Horizontal shear Vertical shear 2D planar transformations See Szeliski Chapter 2 2D planar transformations 2D planar transformations 3D transformation Pinhole Perspective Equation x x ' f ' z y' f ' y z Idealized coordinate system Camera parameters • Intrinsic: relate camera’s coordinate system to the idealized coordinated system • Extrinsic: relate the camera’s coordinate system to a fix world coordinate system • Ignore the lens and nonlinear aberrations for the moment Intrinsic camera parameters Units: k,l : pixel/m f :m (See EXIF tags) a,b: pixel Physical Image Coordinates (f ≠1) Normalized Image Coordinates Scale parameters: k, l (image sensor may not be square) Offset: u0, v0 Manufacturing error: θ Intrinsic camera parameters Calibration matrix κ P ( x, y , z ,1)T The perspective projection Equation In reality • Physical size of pixel and skew are always fixed for a given camera, and in principal known during manufacturing • Some parameters often available in EXIF tag • Focal length may vary for zoom lenses when optical axis is not perpendicular to image plane • Change focus affects the magnification factor • From now on, assume camera is focused at infinity Extrinsic camera parameters Explicit form of projection Matrix riT denotes the i-th row of R, t , t , t , are the coordinates of t x y z T ri can be written in terms of the corresponding angles R can be written as a product of three elementary rotations, and described by three angles M is 3 × 4 matrix with 11 parameters 5 intrinsic parameters: α, β, u0, v0, θ 6 extrinsic parameters: 3 angles defining R and 3 for t Explicit form of projection Matrix Note: M is only defined up to scale in this setting!! riT : i-th row of R Theorem (Faugeras, 1993) Camera parameters A camera is described by several parameters • • • Translation T of the optical center from the origin of world coords Rotation R of the image plane focal length f, principle point (x’c, y’c), pixel size (sx, sy) • blue parameters are called “extrinsics,” red are “intrinsics” Projection equation sx * * * * x sy * * * * s * * * * • • The projection matrix models the cumulative effect of all parameters Useful to decompose into a series of operations identity matrix fsx Π 0 0 0 fsy 0 intrinsics • X Y ΠX Z 1 x'c 1 0 0 0 R y'c 0 1 0 0 3 x 3 0 1 0 0 1 0 1x 3 projection rotation 03 x1 I 3 x 3 1 01x 3 1 T 3 x1 translation Definitions are not completely standardized – especially intrinsics—varies from one book to another Camera calibration toolbox • Matlab toolbox by Jean-Yves Bouguet http://www.vision.caltech.edu/bouguetj/calib_doc/ • Extract corner points from checkerboard