CHAPTER 1 Unit 1: Transformations, Congruence and Similarity
... and y−coordinates changed. Unlike a translation or reflection, a rotation can change both of the coordinates in an ordered pair. Now look closely. One of the points remained exactly the same! We say that we rotated the figure about this point. Imagine you put your finger on this corner of the rectangle ...
... and y−coordinates changed. Unlike a translation or reflection, a rotation can change both of the coordinates in an ordered pair. Now look closely. One of the points remained exactly the same! We say that we rotated the figure about this point. Imagine you put your finger on this corner of the rectangle ...
Applications of Singular-Value Decomposition (SVD)
... f (x) = c1 + c2 x + c3 x2 + · · · + cn xn−1 to some data points {(xi , yi )}, i = 1, . . . , m, where n < m. Compare this with interpolation where we choose the degree n − 1 of the polynomial high enough to pass through all the points; to wit, n = m. A further generalization of the linear least-squa ...
... f (x) = c1 + c2 x + c3 x2 + · · · + cn xn−1 to some data points {(xi , yi )}, i = 1, . . . , m, where n < m. Compare this with interpolation where we choose the degree n − 1 of the polynomial high enough to pass through all the points; to wit, n = m. A further generalization of the linear least-squa ...
Mathematics Essential Curriculum - Eighth Grade Geometry
... leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. Understand similarity in terms of similarity transformations. G.SRT.A.2 Given two figures, use the definition of similarity in terms of similarity transf ...
... leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. Understand similarity in terms of similarity transformations. G.SRT.A.2 Given two figures, use the definition of similarity in terms of similarity transf ...
Mathematics Essential Curriculum - Geometry/Geometry
... line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. Understand similarity in terms of similarity transformations. G.SRT.A.2 Given two figures, use the definition of similarity in terms of similar ...
... line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. Understand similarity in terms of similarity transformations. G.SRT.A.2 Given two figures, use the definition of similarity in terms of similar ...
Unit 1 – Transformations Terms and Definitions
... glossary to be developed during the module. Terms, definitions, and conjectures which arise during the module can be added to the glossary. The activity, which should take no longer than 30 minutes, can be divided up so that each group defines a different set of terms. The terms have been grouped fo ...
... glossary to be developed during the module. Terms, definitions, and conjectures which arise during the module can be added to the glossary. The activity, which should take no longer than 30 minutes, can be divided up so that each group defines a different set of terms. The terms have been grouped fo ...
Transformation geometry
... x As a separate topic in Grade 9, sometimes linked to co-ordinate geometry. Much of this work on transformations has, however, been restricted to the perceptual level, that is, pupils have been given opportunities to physically manipulate figures using cut-outs, paper folding, geoboards, tracings, e ...
... x As a separate topic in Grade 9, sometimes linked to co-ordinate geometry. Much of this work on transformations has, however, been restricted to the perceptual level, that is, pupils have been given opportunities to physically manipulate figures using cut-outs, paper folding, geoboards, tracings, e ...
Geometry Module 2, Topic C, Lesson 12: Teacher
... these concepts via transformations, allowing one to accommodate not only polygonal figures, but also curvilinear figures, in one stroke. Students begin Topic C with an understanding of what similarity transformations are and what it means for figures to be similar. They should see how similarity tra ...
... these concepts via transformations, allowing one to accommodate not only polygonal figures, but also curvilinear figures, in one stroke. Students begin Topic C with an understanding of what similarity transformations are and what it means for figures to be similar. They should see how similarity tra ...
Geometry: Similar Triangles - Math GR. 9-12
... Similar triangles Similar triangles have the same shape, but the size may be different. Two triangles are similar if: • two pairs of corresponding angles are congruent (therefore the third pair of corresponding angles are also congruent). OR • the three pairs of corresponding sides are proportional ...
... Similar triangles Similar triangles have the same shape, but the size may be different. Two triangles are similar if: • two pairs of corresponding angles are congruent (therefore the third pair of corresponding angles are also congruent). OR • the three pairs of corresponding sides are proportional ...
presentation source
... – Safety: avoid writing pixels that aren’t there – Efficiency: save computation cost of rasterizing primitives outside the field of view ...
... – Safety: avoid writing pixels that aren’t there – Efficiency: save computation cost of rasterizing primitives outside the field of view ...
Perspective Nonrigid Shape and Motion Recovery
... that iterative schemes are often very sensitive to initialization. In the rigid case the projective depths can be initialized using algebraic methods based on two-view geometry. In the nonrigid case, the situation is obviously not as straightforward, and hence the method of [12] simply assumes the i ...
... that iterative schemes are often very sensitive to initialization. In the rigid case the projective depths can be initialized using algebraic methods based on two-view geometry. In the nonrigid case, the situation is obviously not as straightforward, and hence the method of [12] simply assumes the i ...
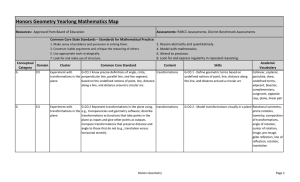
Honors Geometry Yearlong Curriculum Map
... the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. Find arc lengths and G-C.5 Derive using similarity the fact that the length of areas of sectors of the arc interc ...
... the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. Find arc lengths and G-C.5 Derive using similarity the fact that the length of areas of sectors of the arc interc ...