Geometry – Unit One
... G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G.CO.2 Represent transformations in the plane using, e.g., transparencies and geometry sof ...
... G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G.CO.2 Represent transformations in the plane using, e.g., transparencies and geometry sof ...
remarks on the topologies for minkowski space-time
... The conditions that should be satisfied by any topology for Minkowski spacetime were formulated in [6], and they are: (1) The causal order can be deduced from the considered topology, and (2) The group of homeomorphisms of the considered topology is generated by the inhomogeneous Lorentz group and d ...
... The conditions that should be satisfied by any topology for Minkowski spacetime were formulated in [6], and they are: (1) The causal order can be deduced from the considered topology, and (2) The group of homeomorphisms of the considered topology is generated by the inhomogeneous Lorentz group and d ...
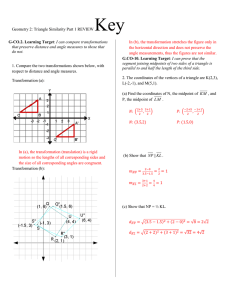
Geometry 2: Triangle Similarity Part 1 REVIEW Key G
... segment joining midpoints of two sides of a triangle is parallel to and half the length of the third side. 2. The coordinates of the vertices of a triangle are K(2,3), L(-2,-1), and M(5,1). (a) Find the coordinates of N, the midpoint of KM , and P, the midpoint of LM . ...
... segment joining midpoints of two sides of a triangle is parallel to and half the length of the third side. 2. The coordinates of the vertices of a triangle are K(2,3), L(-2,-1), and M(5,1). (a) Find the coordinates of N, the midpoint of KM , and P, the midpoint of LM . ...
Hamilton`s principle
... whenever the transformations can be written in terms of some F, then the Hamilton’s equations hold for new coordinates and momenta with the new Hamiltonian! F is the generator of the canonical transformation (in practice, not easy to determine if such a function exists) ...
... whenever the transformations can be written in terms of some F, then the Hamilton’s equations hold for new coordinates and momenta with the new Hamiltonian! F is the generator of the canonical transformation (in practice, not easy to determine if such a function exists) ...
Week 8 2.20.17-2.24.17 - GSE ANALYTIC GEOMETRY
... Georgia Performance Standards: • know that rigid transformations preserve size and shape or distance and angle; use this fact to connect the idea of congruency and develop the definition of congruent • use the definition of congruence, based on rigid motion, to show two triangles are congruent if an ...
... Georgia Performance Standards: • know that rigid transformations preserve size and shape or distance and angle; use this fact to connect the idea of congruency and develop the definition of congruent • use the definition of congruence, based on rigid motion, to show two triangles are congruent if an ...
Document
... We will consider effect of uniform motion on different quantities & laws of physics. We will establish a relationship between the space & time coordinates in two inertial frames of reference. The basic relations were obtained by Galileo & are known as Galilean Transformation Equations. allow us to d ...
... We will consider effect of uniform motion on different quantities & laws of physics. We will establish a relationship between the space & time coordinates in two inertial frames of reference. The basic relations were obtained by Galileo & are known as Galilean Transformation Equations. allow us to d ...
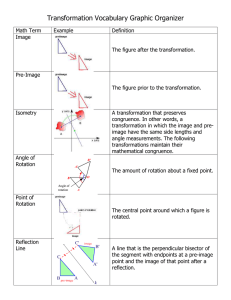
transformations vocabulary review
... A fixed point in the plane about which all points are expanded or contracted. It is the only invariant point under a dilation. A dilation of scalar factor k whose center of dilation is the origin may be written: Dk (x, y) = (kx, ky). If the scale factor, k, is greater than 1, the image is an enlarge ...
... A fixed point in the plane about which all points are expanded or contracted. It is the only invariant point under a dilation. A dilation of scalar factor k whose center of dilation is the origin may be written: Dk (x, y) = (kx, ky). If the scale factor, k, is greater than 1, the image is an enlarge ...
Slide - faculty.ucmerced.edu
... • Focal length may vary for zoom lenses when optical axis is not perpendicular to image plane • Change focus affects the magnification factor • From now on, assume camera is focused at infinity ...
... • Focal length may vary for zoom lenses when optical axis is not perpendicular to image plane • Change focus affects the magnification factor • From now on, assume camera is focused at infinity ...
Transformations
... Common square matrices: Zero matrix: a square matrix with all 0’s. Identity matrix: all 0’s, except elements along the main diagonal which are 1’s. The diagonal of a square matrix: ...
... Common square matrices: Zero matrix: a square matrix with all 0’s. Identity matrix: all 0’s, except elements along the main diagonal which are 1’s. The diagonal of a square matrix: ...
File
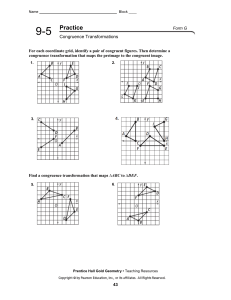
... 8.G ─ Understand congruence and similarity using physical models, transparencies, or geometry software. 2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figu ...
... 8.G ─ Understand congruence and similarity using physical models, transparencies, or geometry software. 2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figu ...
Sect. 7.4 - TTU Physics
... • It’s conventional now to consider the mass m as the same as it is in Newtonian mechanics; as an invariant, intrinsic property of a body. So, the mass m in (1) is same as Newtonian mass and it is the MOMENTUM which is Relativistic! • Using the definition (1) of Relativistic Momentum, it can be show ...
... • It’s conventional now to consider the mass m as the same as it is in Newtonian mechanics; as an invariant, intrinsic property of a body. So, the mass m in (1) is same as Newtonian mass and it is the MOMENTUM which is Relativistic! • Using the definition (1) of Relativistic Momentum, it can be show ...
CMP2: Kaleidoscopes, Hubcaps, and Mirrors (8th) Goals
... Make figures with specified symmetries. Identify a basic design element that can be used with a transformation to replicate a given design. Perform symmetry transformations of figures, including reflections, translations, and rotations. Examine and describe the symmetries of a design made from a fig ...
... Make figures with specified symmetries. Identify a basic design element that can be used with a transformation to replicate a given design. Perform symmetry transformations of figures, including reflections, translations, and rotations. Examine and describe the symmetries of a design made from a fig ...
Document
... For column matrix representation of coordinate positions, we form composite transformations by multiplying matrices in order from right to left. That is, each successive transformation matrix premultiplies the product of the ...
... For column matrix representation of coordinate positions, we form composite transformations by multiplying matrices in order from right to left. That is, each successive transformation matrix premultiplies the product of the ...
Unit 5
... polygon that carry it onto itself Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines and line segments Given a geometric figure and a rotation, reflection or translation, draw the transformed figure-specify a sequence of t ...
... polygon that carry it onto itself Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines and line segments Given a geometric figure and a rotation, reflection or translation, draw the transformed figure-specify a sequence of t ...