Roselle School District Grade 7 Pre-Algebra Honors Curriculum Unit
... and transform it using all three basic transformations Create their geometric figures with rulers and pencils on graph paper using an x, y coordinate grid (interval is to be determined by student) 2. Students will begin using the n-sided figure to perform basic transformations All transformations ...
... and transform it using all three basic transformations Create their geometric figures with rulers and pencils on graph paper using an x, y coordinate grid (interval is to be determined by student) 2. Students will begin using the n-sided figure to perform basic transformations All transformations ...
- Alpine Secondary Math CCSS Resources
... based on the undefined notions of point, line, distance along a line, and distance around a circular arc. line and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G.CO.2 Represent transformations in the plane using, e.g., transp ...
... based on the undefined notions of point, line, distance along a line, and distance around a circular arc. line and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G.CO.2 Represent transformations in the plane using, e.g., transp ...
1. What is meant by spacetime?
... a circle of radius r is 2πr. Open: Angles in a triangle add up to less than 180 degrees. Parallel lines diverge. The circumference of a circle of radius r is less than 2πr. Closed: Angles in a trainagle add up to more than 180 degrees. Parallel lines converge. The circumference of a circle of radius ...
... a circle of radius r is 2πr. Open: Angles in a triangle add up to less than 180 degrees. Parallel lines diverge. The circumference of a circle of radius r is less than 2πr. Closed: Angles in a trainagle add up to more than 180 degrees. Parallel lines converge. The circumference of a circle of radius ...
8-5: Butterflies, Pinwheels, and Wallpaper
... 1. How would you explain what it means for two geometric shapes to be similar using 1a. everyday words that most people could understand? 1b. technical terms of mathematics? ...
... 1. How would you explain what it means for two geometric shapes to be similar using 1a. everyday words that most people could understand? 1b. technical terms of mathematics? ...
view solutions for these.
... Solution. (a) S cannot be a basis for V because it is not independent: v3 = v1 − v2 . (b) Discard the vector v3 . The new set {v1 , v2 } is easily seen to be independent (we know from trigonometry that neither of these functions is a scalar multiple of the other). Moreover it has the same span as th ...
... Solution. (a) S cannot be a basis for V because it is not independent: v3 = v1 − v2 . (b) Discard the vector v3 . The new set {v1 , v2 } is easily seen to be independent (we know from trigonometry that neither of these functions is a scalar multiple of the other). Moreover it has the same span as th ...
x and y - Ninova
... and H, point c, and free vector a. Intuitively, it is helpful to think of a as being attached to the point c. This notion may be formalized by defining yet another entity, called an applied vector, which consists of a pair (p, x), where p is a point and x a free vector. Equivalently, we can define a ...
... and H, point c, and free vector a. Intuitively, it is helpful to think of a as being attached to the point c. This notion may be formalized by defining yet another entity, called an applied vector, which consists of a pair (p, x), where p is a point and x a free vector. Equivalently, we can define a ...
Topics in Applied Mathematics I
... (b) Two sides of the triangle are ~u = (−2, 2, 0)−(0, 0, 5) = (−2, 2, −5) and ~v = (3, −4, 0) − (0, 0, 5) = (3, −4, −5). Then 12 ~v × ~u, which equals (15, 25/2, −1), is a vector perpendicular to the triangle with length equal to the area of the triangle. The flux of air through the triangle equals ...
... (b) Two sides of the triangle are ~u = (−2, 2, 0)−(0, 0, 5) = (−2, 2, −5) and ~v = (3, −4, 0) − (0, 0, 5) = (3, −4, −5). Then 12 ~v × ~u, which equals (15, 25/2, −1), is a vector perpendicular to the triangle with length equal to the area of the triangle. The flux of air through the triangle equals ...
Geometry Unit 2 Overview Sheet Basic Definitions and Rigid Motion
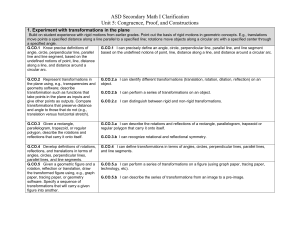
... G.CO.1. Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. I can define angle, circle, perpendicular line, parallel line, and line segment. I can und ...
... G.CO.1. Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. I can define angle, circle, perpendicular line, parallel line, and line segment. I can und ...
Secondary I, 2015-2016 Pacing Guide: Instructional Block 4, 30
... G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G.CO.2: Represent transformations in the plane using, e.g., transparencies and geometry so ...
... G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G.CO.2: Represent transformations in the plane using, e.g., transparencies and geometry so ...
Common Core Geometry
... Undefined termsLay out the basic elements of geometry - the undefined terms of point, line and plane. Introductory DefinitionsDefine bisector, vertex, polygons, and the relationships of parallel and perpendicular. Basic ConstructionsPerform the basic constructions using a variety of tools such as: c ...
... Undefined termsLay out the basic elements of geometry - the undefined terms of point, line and plane. Introductory DefinitionsDefine bisector, vertex, polygons, and the relationships of parallel and perpendicular. Basic ConstructionsPerform the basic constructions using a variety of tools such as: c ...
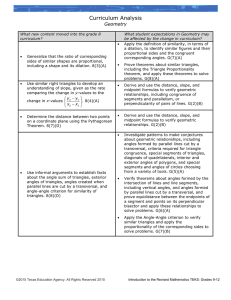
Curriculum Analysis
... about the angle sum of triangles, exterior angles of triangles, angles created when parallel lines are cut by a transversal, and angle-angle criterion for similarity of triangles. 8(8)(D) ...
... about the angle sum of triangles, exterior angles of triangles, angles created when parallel lines are cut by a transversal, and angle-angle criterion for similarity of triangles. 8(8)(D) ...
Transformation rules and matrices
... A transformation rule is a description of a transformation that tells how to get the output point for any given input point. The following notation is typically used: (x, y) stands for the input point. (x′, y′) stands for the output point, also called the image. One way to give a transformation rule ...
... A transformation rule is a description of a transformation that tells how to get the output point for any given input point. The following notation is typically used: (x, y) stands for the input point. (x′, y′) stands for the output point, also called the image. One way to give a transformation rule ...
Content Area
... Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation v ...
... Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation v ...