* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
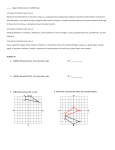
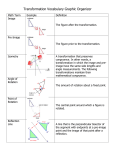
Download GSE Geometry Unit 1: Transformations in the Coordinate Plane
Projective plane wikipedia , lookup
Analytic geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of geometry wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Rotation matrix wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Multilateration wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
Möbius transformation wikipedia , lookup
Lie sphere geometry wikipedia , lookup
Euler angles wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
Lorentz transformation wikipedia , lookup
Plane of rotation wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Rotation group SO(3) wikipedia , lookup