Download Use the Quadratic Formula - Gloucester Township Public Schools

Over Lesson 9–4
Over Lesson 9–4
Solving Quadratic
Equations Using the
Quadratic Formula
Lesson 9-5
• Understand how to solve quadratic
equations by using the Quadratic
Formula.
• Understand how to use the
discriminant to determine the
number of solutions of a quadratic
equation.
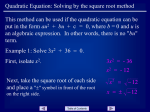
Use the Quadratic Formula
Solve x2 – 2x = 35 by using the Quadratic Formula.
Step 1 Rewrite the equation in standard form.
x2 – 2x = 35
x2 – 2x – 35 = 0
Original equation
Subtract 35 from each side.
Use the Quadratic Formula
Step 2 Apply the Quadratic Formula to find the
solutions.
Quadratic Formula
a = 1, b = –2,
and c = –35
Multiply.
Use the Quadratic Formula
Add.
Simplify.
Separate the
solutions.
or
=7
= –5
Answer: The solutions are –5 and 7.
Solve x2 + x – 30 = 0. Round to the nearest tenth if
necessary.
A. {6, –5}
B. {–6, 5}
C. {6, 5}
D. Ø
Use the Quadratic Formula
A. Solve 2x2 – 2x – 5 = 0 by using the Quadratic
Formula. Round to the nearest tenth if necessary.
For the equation, a = 2, b = –2, and c = –5.
Quadratic Formula
a = 2, b = –2, c = –5
Multiply.
Use the Quadratic Formula
Add and simplify.
or x
x
≈ 2.2
Separate the solutions.
≈ –1.2
Simplify.
Answer: The solutions are about 2.2 and –1.2
Use the Quadratic Formula
B. Solve 5x2 – 8x = 4 by using the Quadratic
Formula. Round to the nearest tenth if necessary.
Step 1
Rewrite equation in standard form.
5x2 – 8x = 4
5x2 – 8x – 4 = 0
Step 2
Original equation
Subtract 4 from each
side.
Apply the Quadratic Formula to find the
solutions.
Quadratic Formula
Use the Quadratic Formula
a = 5, b = –8, c = –4
Multiply.
or
Add and simplify.
or x
x
=2
Separate the solutions.
= –0.4
Simplify.
Answer: The solutions are 2 and –0.4.
A. Solve 5x2 + 3x – 8. Round to the nearest tenth if
necessary.
A. 1, –1.6
B. –0.5, 1.2
C. 0.6, 1.8
D. –1, 1.4
B. Solve 3x2 – 6x + 2. Round to the nearest tenth if
necessary.
A. –0.1, 0.9
B. –0.5, 1.2
C. 0.6, 1.8
D. 0.4, 1.6
Solve Quadratic Equations Using Different
Methods
Solve 3x2 – 5x = 12.
Method 1
Graphing
Rewrite the equation in standard form.
3x2 – 5x = 12
3x2 – 5x – 12 = 0
Original equation
Subtract 12 from
each side.
Solve Quadratic Equations Using Different
Methods
Graph the related function.
f(x) = 3x2 – 5x – 12
Locate the x-intercepts of the
graph.
4.
The solutions are 3 and – __
3
Solve Quadratic Equations Using Different
Methods
Method 2
Factoring
3x2 – 5x = 12
Original equation
3x2 – 5x – 12 = 0
Subtract 12 from
each side.
(x – 3)(3x + 4) = 0
Factor.
x – 3 = 0 or 3x + 4 = 0
x =3
4
x = – __
3
Zero Product
Property
Solve for x.
Solve Quadratic Equations Using Different
Methods
Method 3
Completing the Square
3x2 – 5x = 12
Original equation
Divide each side
by 3.
Simplify.
Solve Quadratic Equations Using Different
Methods
Take the square
root of each side.
Separate the
solutions.
=3
4
= – __
3
Simplify.
Solve Quadratic Equations Using Different
Methods
Method 4
Quadratic Formula
From Method 1, the standard form of the equation is
3x2 – 5x – 12 = 0.
Quadratic Formula
a = 3, b = –5,
c = –12
Multiply.
Solve Quadratic Equations Using Different
Methods
Add and simplify.
x
Separate the
solutions.
x
=3
4
= – __
3
Simplify.
4.
Answer: The solutions are 3 and – __
3
Solve 6x2 + x = 2 by any method.
A. –0.8, 1.4
1
2 , __
B. – __
3 2
4 ,1
C. – __
3
D. 0.6, 2.2
Use the Discriminant
State the value of the discriminant for
3x2 + 10x = 12. Then determine the number of
real solutions of the equation.
Step 1
Rewrite the equation in standard form.
3x2 + 10x = 12
Original equation
3x2 + 10x – 12 = 12 – 12
Subtract 12 from each
side.
3x2 + 10x – 12 = 0
Simplify.
Use the Discriminant
Step 2
Find the discriminant.
b2 – 4ac = (10)2 – 4(3)(–12)
= 244
a = 3, b = 10, and
c = –12
Simplify.
Answer: The discriminant is 244. Since the discriminant
is positive, the equation has two real solutions.
State the value of the discriminant for the equation
x2 + 2x + 2 = 0. Then determine the number of real
solutions of the equation.
A. –4; no real solutions
B. 4; 2 real solutions
C. 0; 1 real solutions
D. cannot be determined
Homework
Page 587 #17-49 odd