![arXiv:1510.01797v3 [math.CT] 21 Apr 2016 - Mathematik, Uni](http://s1.studyres.com/store/data/003897650_1-5601c13b5f003f1ac843965b9f00c683-300x300.png)
The Proof Complexity of Polynomial Identities
... known about the complexity of propositional Frege proofs. The Frege proof system for propositional logic can be seen as a straightforward extension of the equational proof system considered in this paper, when taken over the field F2 . Thus, a progress in understanding the latter system can potentia ...
... known about the complexity of propositional Frege proofs. The Frege proof system for propositional logic can be seen as a straightforward extension of the equational proof system considered in this paper, when taken over the field F2 . Thus, a progress in understanding the latter system can potentia ...
Polynomial Size Proofs for the Propositional Pigeonhole Principle
... Case 2 A is a formula A1 ∨ A2 . a. If τ (A) = 1, then the induction hypothesis states that either B1 , . . . , Bn ` A1 or B1 , . . . , Bn ` A2 . If the first is the case, we can use Axiom 3 to get B1 , . . . , Bn ` A1 ∨ A2 . In the latter case, we can use Axiom 4 to get B1 , . . . , Bn ` A1 ∨ A2 . ...
... Case 2 A is a formula A1 ∨ A2 . a. If τ (A) = 1, then the induction hypothesis states that either B1 , . . . , Bn ` A1 or B1 , . . . , Bn ` A2 . If the first is the case, we can use Axiom 3 to get B1 , . . . , Bn ` A1 ∨ A2 . In the latter case, we can use Axiom 4 to get B1 , . . . , Bn ` A1 ∨ A2 . ...
Universal enveloping algebras and some applications in physics
... to motivate the introduction of enveloping algebras. The Baker-CampbellHaussdorff formula is presented since it is used in the second section where the definitions and main elementary results on universal enveloping algebras (such as the Poincaré-Birkhoff-Witt) are reviewed in details. Explicit for ...
... to motivate the introduction of enveloping algebras. The Baker-CampbellHaussdorff formula is presented since it is used in the second section where the definitions and main elementary results on universal enveloping algebras (such as the Poincaré-Birkhoff-Witt) are reviewed in details. Explicit for ...
on h1 of finite dimensional algebras
... a) The zero ideal is pre-generated whenever Q has no oriented cycles. b) Consider an admissible two-sided ideal which is either “full or zero” between each couple of vertices x and y. More precisely, either yIx = ykQx or yIx = 0. Then I is pre-generated. c) A quiver is said to be narrow if for any c ...
... a) The zero ideal is pre-generated whenever Q has no oriented cycles. b) Consider an admissible two-sided ideal which is either “full or zero” between each couple of vertices x and y. More precisely, either yIx = ykQx or yIx = 0. Then I is pre-generated. c) A quiver is said to be narrow if for any c ...
Acta Acad. Paed. Agriensis, Sectio Mathematicae 27 (2000) 25–38
... that the above triangle is right angled, so its R is equal to half of its hypothenuse. It is now clear that if k is an arbitrary positive integer which is a multiple of p, then there exists a Heron triangle of radius R = k. To see this, it suffices to consider the triangle which is similar to the tria ...
... that the above triangle is right angled, so its R is equal to half of its hypothenuse. It is now clear that if k is an arbitrary positive integer which is a multiple of p, then there exists a Heron triangle of radius R = k. To see this, it suffices to consider the triangle which is similar to the tria ...
BOOLEAN ALGEBRA Boolean algebra, or the algebra of logic, was
... Ω1×… × Ωn. Each subset X of this Cartesian product is correlated with a proposition PX concerning the state x of S, namely the assertion that the n-tuple of measured values of f1,...,fn lies in X when S in state x. X then has a representative X in Σ defined by X = {x∈Σ: (f1(x),...,fn(x)) ∈ X}. Thus ...
... Ω1×… × Ωn. Each subset X of this Cartesian product is correlated with a proposition PX concerning the state x of S, namely the assertion that the n-tuple of measured values of f1,...,fn lies in X when S in state x. X then has a representative X in Σ defined by X = {x∈Σ: (f1(x),...,fn(x)) ∈ X}. Thus ...
An efficient algorithm for computing the Baker–Campbell–Hausdorff
... may consider an approximation of the form ⌿h ⬅ exp共ha1A兲exp共hb1B兲 ¯ exp共hakA兲exp共hbkB兲 for the exact flow exp共h共A + B兲兲 of 共1.5兲 after a time step h. The idea now is to obtain the conditions to be satisfied by the coefficients ai, bi so that ⌿h共q兲 = u共h兲 + O共h p+1兲 as h → 0, and this can be done by ...
... may consider an approximation of the form ⌿h ⬅ exp共ha1A兲exp共hb1B兲 ¯ exp共hakA兲exp共hbkB兲 for the exact flow exp共h共A + B兲兲 of 共1.5兲 after a time step h. The idea now is to obtain the conditions to be satisfied by the coefficients ai, bi so that ⌿h共q兲 = u共h兲 + O共h p+1兲 as h → 0, and this can be done by ...
Math 112 Quadratics Notes
... of best fit for a quadratic always generates a curve that will have a maximum or minimum value. There are three ways of obtaining this maximum or minimum value: 1) Press Trace then move the “x” displayed on your graph left or right until it is centered over the max (or min) value. Read the coordinat ...
... of best fit for a quadratic always generates a curve that will have a maximum or minimum value. There are three ways of obtaining this maximum or minimum value: 1) Press Trace then move the “x” displayed on your graph left or right until it is centered over the max (or min) value. Read the coordinat ...
Transcript - MIT OpenCourseWare
... Now, the question asked you to compute this gradient at the particular point minus 1, 2. So we have gradient of f at the point minus 1, 2 is equal to-- well, we just put in x equal minus 1, y equal 2 into this formula. So at x equal minus 1, y equals 2, this is 2 times minus 1 times 2 plus 2 square ...
... Now, the question asked you to compute this gradient at the particular point minus 1, 2. So we have gradient of f at the point minus 1, 2 is equal to-- well, we just put in x equal minus 1, y equal 2 into this formula. So at x equal minus 1, y equals 2, this is 2 times minus 1 times 2 plus 2 square ...
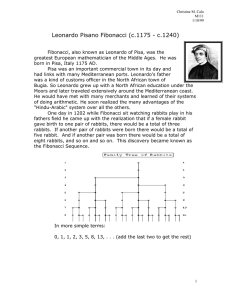
Leonardo Pisano Fibonacci (c.1175 - c.1240)
... Fib(n) = -----------------sqrt(5) If you don't like negative powers then we can use x-n=(1/x)n: Phin - (- 1/Phi)n Fib(n) = ------------------sqrt(5) If you also don't like taking reciprocals then we can use phi=1/Phi and the formula can be written as: Phin - (-phi)n Fib(n) = ---------------sqrt(5) H ...
... Fib(n) = -----------------sqrt(5) If you don't like negative powers then we can use x-n=(1/x)n: Phin - (- 1/Phi)n Fib(n) = ------------------sqrt(5) If you also don't like taking reciprocals then we can use phi=1/Phi and the formula can be written as: Phin - (-phi)n Fib(n) = ---------------sqrt(5) H ...
Automatic differentiation

In mathematics and computer algebra, automatic differentiation (AD), also called algorithmic differentiation or computational differentiation, is a set of techniques to numerically evaluate the derivative of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions (exp, log, sin, cos, etc.). By applying the chain rule repeatedly to these operations, derivatives of arbitrary order can be computed automatically, accurately to working precision, and using at most a small constant factor more arithmetic operations than the original program.Automatic differentiation is not: Symbolic differentiation, nor Numerical differentiation (the method of finite differences).These classical methods run into problems: symbolic differentiation leads to inefficient code (unless carefully done) and faces the difficulty of converting a computer program into a single expression, while numerical differentiation can introduce round-off errors in the discretization process and cancellation. Both classical methods have problems with calculating higher derivatives, where the complexity and errors increase. Finally, both classical methods are slow at computing the partial derivatives of a function with respect to many inputs, as is needed for gradient-based optimization algorithms. Automatic differentiation solves all of these problems.