* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Introduction to Op-Amp
Public address system wikipedia , lookup
Electrical ballast wikipedia , lookup
History of electric power transmission wikipedia , lookup
Flip-flop (electronics) wikipedia , lookup
Electrical substation wikipedia , lookup
Ground loop (electricity) wikipedia , lookup
Scattering parameters wikipedia , lookup
Audio power wikipedia , lookup
Dynamic range compression wikipedia , lookup
Power inverter wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Signal-flow graph wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Control system wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
Current source wikipedia , lookup
Surge protector wikipedia , lookup
Two-port network wikipedia , lookup
Alternating current wikipedia , lookup
Stray voltage wikipedia , lookup
Integrating ADC wikipedia , lookup
Power electronics wikipedia , lookup
Regenerative circuit wikipedia , lookup
Negative feedback wikipedia , lookup
Voltage optimisation wikipedia , lookup
Buck converter wikipedia , lookup
Mains electricity wikipedia , lookup
Voltage regulator wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Current mirror wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
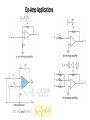
EE 174 Spring 2017 Operational Amplifiers Contents • Introduction • Brief of History • Fundamentals of Op-Amps • Basic operation • Gain • Offset • Applications Introduction • Operational Amplifier (Op-Amp) name comes from the fact that it was originally used to perform mathematical operations. • Op-Amp is an active circuit element which is basic component used to build analog circuits. • Op-Amp is a low cost integrating circuit consisting of transistors, resistors, diodes and capacitors. • Op-Amp amplify an input signal produces an output voltage equal to the difference between the two input terminals multiplied by the gain A. • Op-Amps are two-port networks in which the output voltage or current is directly proportional to either input voltage or current. Four different kind of amplifiers exits: • • • • Voltage amplifier: Av = Vo / Vi Current amplifier: Ai = Io / Ii Transconductance amplifier: Gm = Io / Vi Transresistance amplifier: Rm = Vo / Ii • The op-amp always “wants” both inputs (inverting and non-inverting) to be the same value. If they are not, the same value, the op amp output will go positive or negative saturation, depending on which input is higher than the other. • Op-Amps are commonly used for both linear and nonlinear applications: Inverting/Non-inverting Amplifiers, Variable Gains Amplifiers, Summers, Integrators/Differentiators, Filters (High, Low, Band Pass and Notch Filters), Schmitt trigger, Comparators, A/D converters. Brief History of Op-Amp Monolithic IC Op-Amp Vacuum Tube Op-Amps (1930’s-1940’s) Solid State Discrete Op-Amps Dual-supply voltage of +300/-300 V (1960’s) Output swing +/- 50 volts Open-loop voltage gain of 15,000 to 20,000, Slew rate of +/- 12 volts/µsecond Maximum output current of 1 mA George Philbrick Dual-supply voltage of +15/-15 V Output swing +/- 11 volts Open-loop voltage gain of 40,000, Slew rate of +/- 1.5 volts/µsecond Maximum output current of 2.2 mA • First created in 1963 μA702 by Fairchild Semiconductor • μA741 created in 1968, became widely used due to its ease of use 8 pin, dual in-line package (DIP) • Further advancements include use of field effects transistors (FET), greater precision, faster response, and smaller packaging Internal Op-Amp Circuits Op-Amp Ideal, Equivalent Circuit, Characteristics and Features Ideal Op-Amp Op-Amp Equivalent Circuit Op-Amp Characteristics Op-Amp Symbol 741 Op-Amp Features +V2: Non-inverting input -V1: Inverting input +Vs: Positive source PS -Vs: Negative source PS Vout: Output voltage ON: Offset Null NC: Not Connected The Ideal Op-Amp Assumptions vd = v+ - vvo = Avd = A(v+ – v-) Note: v+ = v2, v- = v1 1) The input impedance Ri is infinite - i.e. no current flows into either input. 2) The output impedance Ro is zero - i.e. the op-amp can drive any load impedance to any voltage. 3) The open-loop gain (A) is infinite. 4) The bandwidth is infinite. 5) The output voltage is zero when the input voltage difference is zero. 6) The slew rate is infinite Op-Amp Two Basic Operations The Inverting Op Amp The Non-inverting Op Amp The op-amp always “wants” both inputs (inverting and non-inverting) to be the same value. Op-Amp Gain Open loop gain: This form of gain is measured when no feedback is applied to the op amp. Closed loop gain: This form of gain is measured when the feedback loop is closed and the overall gain of the circuit is much reduced. It has two forms, signal gain and noise gain. The expression for the gain of a closed-loop amplifier involves the open-loop gain. If G is the actual gain, NG is the noise gain, and AVOL is the open-loop gain of the amplifier, then: G = NG 0 Since the open-loop gain AVOL is very high, the closed-loop gain of the circuit is simply the noise gain, G = NG. Loop gain: The difference between the open-loop gain and the closed-loop gain is known as the loop gain. This is useful information because it gives you the amount of negative feedback that can apply to the amplifier system. Signal Gain and Noise Gain Signal gain: This is the gain applied to the input signal, with the feedback loop connected. It can be inverting or non-inverting. It can even be less than unity for the inverting case. Signal gain is the gain that we are primarily interested in when designing circuits. Noise gain: Noise gain is the reciprocal of the attenuation from the output of an op amp (or any feedback loop) to the input. This is the gain applied to a noise source in series with an op amp input. It is also the gain applied to an offset voltage. It is the same for either an inverting or non-inverting stage. It is the noise gain that is used to determine stability. Summary of Signal Gain and Noise Gain Note: Voltage sources are grounded when calculating noise gain in op-amp. The attenuation is R1/(R1 + R2) The noise gain is (R2 + R1)/R1 Op-Amp Gain and Bandwidth The Voltage Gain (A) of the operational amplifier can be found using the following formula: and in Decibels or (dB) is given as: Gain versus Bandwidth Applying feedback will reduce the gain but increase the bandwidth. Gain Bandwidth Product (GBP) Gain-bandwidth (GBW) product is defined as the op-amp gain multiplied by the bandwidth. The GBW product can be used to calculate the closedloop gain bandwidth. GBW = A x BW where A is in ratio (not in dB) GBW/closed-loop gain = closed-loop BW Closed-loop BW = GBW / A Examples: The GBW @ unity gain (from graph) GBW = 1 x 10 MHz = 10 MHz The GBW @ closed-loop gain A = 100 GBW = 100 x 100 KHz = 10 MHz BW = 1 MHz, closed-loop gain? A = GBW / BW = 10 MHz / 1MHz = 10 Closed loop gain 70 dB. Closed-loop BW? Gain: 20 log A = 70 dB log A = 70/20 = 3.5 or A = 103.5 = 3162 Closed-loop BW = 10 MHz / 3162 = 3163 Hz Bode Plot Example Given a transfer function: H(s) = = 100 100 = 𝑠 𝑠+30 30 (30 +1) 100 1 1 = 3.3 𝑠 𝑠 30 ( +1) ( +1) 30 30 Constant gain = 3.3 Gain in dB = 20 log (3.3) ≈ 10 dB Pole at 30 rad/sec Phase = 45o at 30 rad/sec Op-Amp Saturation The op amp has three distinct regions of operation: • Linear region: −Vsat_L- < Vo < Vsat_L+ • Positive saturation: Vo > Vsat_L+ • Negative saturation: Vo < −Vsat_LThe output voltage of a practical amplifier cannot exceed certain threshold value is called saturation. A voltage amplifier behaves linearly, i.e., Vo/Vi = Av = constant as long as the output voltage remains below the “saturation” voltage, −Vsat_L- < Vo < Vsat_L+ Note that the saturation voltage, in general, is not symmetric. For an amplifier with a given gain, Av, the above range of Vo translate into a certain range for Vi − Vsat_L- < Vo < Vsat_L+ − Vsat_L- < Av Vi < Vsat_L+ − Vsat_L- / Av < Vi < Vsat_L+ / Av Any amplifier will enter its saturation region if Vi is raised above certain limit. The figure shows how the amplifier output clips when amplifier is not in the linear region. Vsat_L+ Vsat_L- Example: For Av = 105, Vsat_L- = -12V, Vsat_L+ = +15V, find range of input Vi to prevent saturation. Solution: -12V / 105 < Vi < 15V / 105 or -0.12mV < Vi < 0.15mV Maximum Output Voltage Swing The maximum output voltage, VOM±, is defined as “the maximum positive or negative peak output voltage that can be obtained without wave form clipping when quiescent DC output voltage is zero”. VOM± is limited by the output impedance of the amplifier, the saturation voltage of the output transistors, and the power supply voltages. Note that VOM± depends on the output load. The maximum value that VBQ6 can be is +VCC, therefore VO ≤ +VCC – VR1 – VBEQ6 – VSATQ6. The minimum value that Vi can be is –VEE, therefore VO ≥ –VEE + VR2 + VBEQ7 + VSATQ7. This emitter follower structure cannot drive the output voltage to either rail. Rail to rail output op amps use a common emitter (bipolar) or common source (CMOS) output stage. With these structures, the output voltage swing is only limited by the saturation voltage (bipolar) or the on resistance (CMOS) of the output transistors, and the load being driven. Op-Amp slew rate basics Square Wave: The slew rate (SR)of an op amp is the rate of change in the output voltage caused by a step change on the input. It is measured as a voltage change in a given time - typically V / µs. The slew rate may be very important in many applications. For the given graph, it takes 2 µs to swing 10 V so SR = 5V/ µs. Sine Waves: The maximum rate of change for a sine wave occurs at the zero crossing and may derived as follows: Given vo = VP sin(2π f t) Slew Rate (SR) = V/µs = 2π f VP cos(2π f t) = max = 2π f VP t=0 SR = 2π fmax VP Example: Slew rate S0 = 1 V/μs; input voltage vin (t) = sin(2π × 105t); closed loop gain AV =10. 1) Sketch the theoretically correct output and the actual output of the amplifier in the same graph. 2) What is the maximum frequency that will not violating the given slew rate? Solutions: 1) With the closed-loop voltage gain of 10 vo(t) = 10 sin(2π × 105t) = Aω = A x 2π x f = 10 × 2π × 105 = 6.28 V/μs max 2) fmax = SR / (A x 2π) = 1 x 106 / (10 x 2π) = 15.9 kHz Op-Amp Offset Parameters Another practical concern for op-amp performance is voltage offset. A perfect op-amp would output exactly zero volts with both its inputs shorted together and grounded. However, most op-amps off the shelf will drive their outputs to a saturated level, either negative or positive even if the op-amp in question has zero common-mode gain (infinite CMRR). This deviation from zero is called offset. In the example shown above, the output voltage is saturated at a value of positive 14.7 volts, just a bit less than +V (+15 volts) due to the positive saturation limit of this particular op-amp. Unlike common-mode gain, there are usually provisions made by the manufacturer to trim the offset of a packaged op-amp. Usually, two extra terminals on the op-amp package are reserved for connecting an external “trim” potentiometer. These connection points are labeled offset null and are used in this general way: 741 OPAMP have offset voltage null capability by connecting 10 K ohm pot between pin 1 and pin 5. By varying the potentiometer, output offset voltage (with inputs grounded) can be reduced to zero volts. For the 741C the offset voltage adjustment range is ± 15 mV. Op-Amp Offset Example Example: Determine the output voltage in each of the following cases for the open loop differential amplifier shown below. (a) vin 1 = 5 µVdc, vin 2 = -7 µVdc (b) vin 1 = 10 mV rms, vin 2= 20 mV rms Specifications of the OPAMP are given below: A = 200,000, Ri = 2 MΩ , RO = 75Ω, + VCC = + 15 V, - VEE = - 15 V, and output voltage swing = ± 14V. Solution: (a). The output voltage of an OPAMP is given by Remember that vo = 2.4 V dc with the assumption that the dc output voltage is zero when the input signals are zero. (b). The output voltage equation is valid for both ac and dc input signals. The output voltage is given by Thus the theoretical value of output voltage vo = -2000 V rms. However, the OPAMP saturates at ± 14 V. Therefore, the actual output waveform will be clipped as shown fig. 5. This non-sinusoidal waveform is unacceptable in amplifier applications. Op-Amp Applications Differential Amplifier If R1 = R2 and R3 = R4 Op-Amp Applications Find i, if and vo. i=0A For the ideal op amp shown below, what should be the value of resistor Rf to obtain a gain of 5? Op-Amp Applications 1) Calculate all voltage drops and currents in this circuit, complete with arrows for current direction and polarity markings for voltage polarity. Then, calculate the overall voltage gain of this amplifier circuit (AV), both as a ratio and as a figure in units of decibels (dB): Solutions: Gain = AV = 1.468 = 3.335 dB 2) Given gain RF/RS = 100, GBW product = A0 ω0 = K = 4π × 106 . Determine the overall 3-dB bandwidth of the cascade amplifier Solutions: The 3-dB bandwidth for each amplifier is: below: Thus, the bandwidth of the cascade amplifier is 4π × 104, the cascade amplifier gain is A1A1= 100 × 100 = 104. To achieve the same gain with a single-stage amplifier having the same K, the bandwidth would be Op-Amp Applications Problem: Suppose that we need an amplifier with input resistance of 500 kΩ or greater and a voltage gain of -10. The feedback resistors are to be implemented in integrated form and have values of 10 kΩ or less to conserve chip area. Choose a suitable circuit configuration and specify the resistance values. Solution: Gain of -10 Use inverting Op-Amp where gain A = - R2/R1 = -10 To attain desired input resistance R1 = 500 kΩ R2 = 5MΩ. These values exceed the maximum values allowed. To attain large input resistance with moderate resistances for an inverting amplifier, we cascade a voltage follower with an inverter. To achieve the desired gain = - 10. Choose R1 = 1 kΩ R2 = 10 kΩ. R2 Op-Amp Applications For Rs = 10 kΩ, RL = 1 kΩ VL = 0.1 Vin Huge attenuation of the signal source. If voltage follower (buffer amplifier) is used. VL = Vout = Vin Active Filters, Integrators & Differentiators Consider the circuit shown. Various circuits can be made with different choices for Z1 and Z2. Following the inverting amplifier solution, we find: Active Filters, Integrators & Differentiators Active Filters, Integrators & Differentiators Integrator The Comparators • A comparator is a device with two input terminals, inverting and noninverting, and an output that usually swings from rail to rail. • A comparator has low offset, high gain, and high common-mode rejection. • A comparator has a logic output that indicates which of the two inputs is at a higher potential. If its output is TTL or CMOS compatible (and many comparators are), it is always intended to be at one rail or the other—or making a rapid transition between the two. • Comparators are designed to work as open-loop systems, to drive logic circuits, and to work at high speed, even when overdriven. The Comparators with and without Hysteresis Comparator without Hysteresis This configuration uses a voltage divider (Rx and Ry) to set up the threshold voltage. The comparator will compare the input signal (Vin) to the threshold voltage (Vth). The comparator input signal is applied to the inverting input, so the output will have an inverted polarity. When the Vin > Vth the output will drive to the negative supply (GND or logic low). When Vin < Vth the output will drive to the positive supply (Vcc = 5V or logic high). Comparator with Hysteresis A small change to the comparator circuit can be used to add hysteresis. Hysteresis uses two different threshold voltages to avoid the multiple transitions introduced in the previous circuit. For this inverting comparator, the input signal must exceed the upper threshold (VH) to transition low or below the lower threshold (VL) to transition high. The resistor Rh sets the hysteresis level. When the output is at a logic high (5V), Rh is in parallel with Rx. This drives more current into Ry, raising the threshold voltage (VH) to 2.7V. The input signal will have to drive above VH=2.7V to cause the output to transition to logic low (0V). When the output is at logic low (0V), Rh is in parallel with Ry. This reduces the current into Ry, reducing the threshold voltage to 2.3V. The input signal will have to drive below VL=2.3V to cause the output to transition to logic high (5V). Design of Hysteresis Comparator The design requirements are as follows: • Supply Voltage: +5 V • Input: 0V to 5V • VL (Lower Threshold) = 2.3V • VH (Upper Threshold) = 2.7V • VH - VL = 0.4V • Vth ± 0.2V = 2.5V ± 0.2V Equations (1) and (2) can be used to select the resistors needed to set the hysteresis threshold voltages VH and VL. One value (Rx) must be arbitrarily selected. In this example, Rx was set to 100kΩ to minimize current draw. Rh was calculated to be 575kΩ, so the closest standard value 576kΩ was used Op-amp Comparator Circuit Although op amps are not designed to be used as comparators, there are, nevertheless, many applications where the use of an op amp as a comparator is a proper engineering decision. WHY USE AN OP AMP AS A COMPARATOR? • Convenience • Economy • Low IB • Low VOS There are several reasons to use op amps as comparators. Some are technical, one is purely economic. It is economical to use the spare op amp in a quad as a comparator rather than buying an additional comparator, but this is not a good design practice. WHY NOT USE AN OP AMP AS A COMPARATOR? • Speed • Inconvenient input structures There are several reasons not to use op amps as comparators. First • Inconvenient logic structures and foremost is speed, but there are also output levels, stability (and • Stability/hysteresis hysteresis), and a number of input structure considerations. The Op-Amp Comparators References: • http://www.ume.gatech.edu/mechatronics_course/OpAmp_F08.ppt • http://www.allaboutcircuits.com/textbook/semiconductors/chpt-8/operational-amplifier-models/ • http://www.ti.com/lit/an/slaa068a/slaa068a.pdf • http://www.radio-electronics.com/info/circuits/opamp_basics/operational-amplifier-slew-rate.php • http://www.planetanalog.com/author.asp?section_id=483&doc_id=562347 • http://www-ferp.ucsd.edu/najmabadi/CLASS/ECE60L/02-S/NOTES/opamp.pdf • http://www-inst.eecs.berkeley.edu/~ee105/fa14/lectures/Lecture06-Non-ideal%20Op%20Amps%20(Offset-Slew%20rate).pdf • http://nptel.ac.in/courses/117107094//lecturers/lecture_6/lecture6_page1.htm • http://www.ti.com/ww/en/bobpease/assets/AN-31.pdf • http://www.cs.tut.fi/kurssit/TLT-8016/Chapter2.pdf • http://www.electronics-tutorials.ws/opamp/op-amp-comparator.html • http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/schmitt.html • http://lpsa.swarthmore.edu/Bode/BodeExamples.html • http://www.allaboutcircuits.com/worksheets/inverting-and-noninverting-opamp-voltage-amplifier-circuits/ • Fundamentals of Electrical Engineering, Giorgio Rizzoni, McGraw-Hill Higher Education • http://chrisgammell.com/how-does-an-op-amp-work-part-1/ • http://electronicdesign.com/analog/whats-all-noise-gain-stuff-anyhow • http://howtomechatronics.com/how-it-works/electrical-engineering/schmitt-trigger/ • http://www.analog.com/media/en/training-seminars/design-handbooks/Basic-Linear-Design/Chapter1.pdf • http://www.ti.com/lit/an/sloa011/sloa011.pdf • http://www.analog.com/media/en/technical-documentation/application-notes/AN-849.pdf • http://www.ti.com/lit/ug/tidu020a/tidu020a.pdf