Download Summer Work for Students Entering Physics

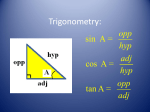
Summer Work for Students Entering Physics
2010-2011
All entering Physics students must be familiar with the following basic math skills, among others,
before the start of the school year. Read the given examples carefully and do all the problems. You
should show your work neatly for all problems throughout the packet. Write all of your final
answers on the answer sheet at the end of the packet. You may consult textbooks and other sources.
The packet will be collected on the first day of class and graded for accuracy.
A. Rounding
B. Multiplying fractions using the calculator
C. Areas of rectangles and volumes of rectangular blocks
D. Exponents
E. Cross multiplication & division
F. Simple Algebra problems
G. Literal equations in Algebra
H. Complex fractions
I. Unit conversion
J. Trigonometry and Geometry
1
A. Rounding
If the next digit is 5 or higher, then round up; if the digit is less than 5, then round down.
Round only once; do not round twice.
e.g.
If you want to round to whole number, then
a)
24.45 = 24
b)
23.67 = 24
c)
1.443 = 1
e.g.
If you want to round to 1 decimal place, then
a)
24.45 = 24.5
b)
23.67 = 23.7
c)
1.443 = 1.4
Do Problems:
1. Round the following numbers to 3 decimal places:
(i)
58.3382
(ii)
2.5546
(iii)
729.5005
(iv)
4.8898
B. Multiplying fractions using the calculator
The parentheses are often used to indicate multiplication.
e.g.
(2.5)(4.6)(6.7) means 2.5 is multiplied by 4.6, which is then multiplied by 6.7
For a fraction, multiply the value above the fraction line and divide the value below the fraction
line.
 1.2  3.4  5.6 
e.g.




 2.3  4.5  6.7 
= 0.33
(a) I suggest you solve the problem above by looking at one pair of parentheses at a time. So
on your calculator, press:
1.2  2.3 x 3.4 4.5 x 5.6  6.7
It is also correct to (b) multiply all the numbers above the fraction line first, then divide by all
the numbers below the fraction line; so on your calculator, press:
1.2 x 3.4 x 5.6  2.3  4.5  6.7
1.2 x 3.4 x 5.6 (2.3 x 4.5 x 6.7)
or (c) press:
(note: the parenthesis)
(d) when multiplying and/or dividing with scientific notation, use parenthesis, or treat each part
of the notation separately.
(4.25) (6.20 x 1012)
(3.42 x 106)
=
(4.25) (6.20) (1012)
(3.42) (106)
2
2. Use method (a) above and your calculator to evaluate the following expressions.
(i)
 8.09  3.23  8.55 




 3.44  4.50  6.73 
(ii)
(iii) (2.96 x 105) (4.3 x 102)
(8.58 x 103)
(iv)
 70.2  5.90  2.35  4.25  10.23 






 3.11  4.23  4.43  6.77  3.76 
(6.67 x 10-11) (423) (570)
(640 x 10-6)2
C. Areas of rectangles and volumes of rectangular blocks
Area of rectangle = length x width
Area of volume of a rectangular box = length x width x height
Note that the units multiply and divide also.
e.g.
If
then
length = 5.02 cm, width = 2.34 cm,
area = (5.02 cm)(2.34 cm)
= 11.7 cm 2
e.g.
If
then
length = 5.02 cm, width = 2.34 cm, height = 1.23 cm,
volume = (5.02 cm)(2.34 cm)(1.23 cm)
= 14.4 cm 3
3. If the length of a rectangle measures 35.6 cm and the width measures 2.30 cm, what is the
area? (Don’t forget to write the unit.) Show work (setup) clearly.
4. A box measures 12.5 cm in length, 8.67 cm in width, and 3.30 cm in height. What is the
volume? Show work (setup) clearly.
3
D. Exponents
a) The value of any power expression with exponent zero is equal to 1, i.e., a 0 =1.
e.g.
10 0 =1
110 =1
230 =1
etc.
b) To multiply two powers having the same base, add the exponents,
i.e.
(a m )(a n )  a mn
e.g.
(32 )(35 )  37
c) To divide one power by another having the same base, subtract the exponents,
am
38
38
mn
6
i.e.
e.g.1.
e.g.2.

a

3
 310
n
2
2
a
3
3
d) To evaluate the power to another power, multiply the exponents,
i.e.
(a m ) n  a mn
e.g.
(32 ) 5 = 310
5. Evaluate the following expressions:
(i)
(iii)
(v)
(53 )(510 )
(ii)
6 24
(iv)
63
10 23
(vi)
10  2
(5a 4 ) 3
10 23
10 11
 513  5 4 



 5 22  5 6 



e) Ten to a negative power gives a number less than 1. Therefore ten to a large negative
power will give a small decimal number.
10-12 < 10-9 < 10-3 < 1 < 103 < 109 < 1012
i.e.
10 6 
“<” sign means “less than”
1
= 0.000001
10 6
6. Which number is larger in each of the following?
(i) 10-8 or 10-5 ?
(ii) 10-4 or 0.1?
4
(iii) 10-3 or 0.01?
E. Cross multiplication & division
D
e.g.
M
V
If D = 3.42 g/mL and V = 12.2 mL, then upon substitution,
3.42
M
M

3.42 =
is the same as
1
12.2
12.2
thus: (1)M = (3.42) (12.2) = 41.7 g
The idea is to put the unknown on one side and everything else on the other side of the equal
sign. Cross multiply 3.42 and 12.2. This is the same as multiplying 12.2 on both sides and then
canceling.
M
3.42 =
12.2
(3.42) (12.2) = M
M = 41.7 g
e.g.
If D = 3.42 g/mL and M = 45.6 g, then upon substitution,
3.42 = 45.6
V

(3.42) V = 45.6

V = 45.6  V = 12.3g
3.42
7. If
M
n
V
and M = 2.1 and V = 3.8, calculate n.
8. If
M
n
V
and M = 2.1 and n = 5.5, calculate V.
5
F. Simple Algebra problems
e.g.
v = v0 + a t
If v = 15 m/s, v0 = 10 m/s, t = 8 s, then write
15 m/s = 10 m/s + a(8 s)
9. GPE = m g h
and
GPE = 450
 a = (15 -10) m/s
8s
m = 24
 a = 0.625 m/s2
g = 9.8
Solve for h. Don’t forget to check your units.
10. v = v0 + a t
and
v = 8 m/s
v0 = 2 m/s
a = 3.5 m/s2
Solve for t. Don’t forget to check your units.
G. Literal equations in Algebra
Express one variable in terms of other variables, without numbers.
e.g.
For the expression,
(a)
express F in terms of the other variables:
(b)
express m in terms of the other variables:
(c)
express v in terms of the other variables:
11. If M1V1  M 2 V2 , express
(i)
V2 in terms of the other variables.
(ii)
M1 in terms of the other variables.
6
Fd = (1/2) mv2
1 / 2mv 2
F
d
2 Fd
m= 2
v
v=
2 Fd
m
12. If M 
n
, express
V
(i)
n in terms of the other variables
(ii)
V in terms of the other variables
H. Complex fractions
The fraction line is a division line. Since
A
means A  B,
B
C
D

E
F
=
C
E

D
F
=
C F
x
D E
Do the same for units.
13. Evaluate the following expressions
(i)
8.566
2.35

15.90
9.33
(ii)
7
3.56
2.00

4.44
9.33
I. Unit conversion
Example 1: Change 26.2 miles to meters.
26.2 mi. x 1609 m
1 mi.
=
42155.8 m
Example 2: Change 4.75 liters to milliliters
4.75 liters x 1 milliliter = 4750 ml = 4.75 x 103 ml
.001 liter
Solve the following conversion problems using multiplication by conversion factors. Equivalent
measurements and metric prefixes can be found on the next page. Please show all of your work in
the space below or on a separate sheet of paper.
14.
45 cm =
?
inches
15.
100 yards =
?
meters
16.
1 mile =
?
kilometers
17.
180 pounds =
18.
1,000,000 newtons =
19.
2 liters =
20.
10 gallons =
21.
400 m =
?
km
22.
500  m =
?
cm
23.
65 kg =
?
grams
?
?
newtons
?
tons
quarts
?
liters
8
Equivalents and Conversion Factors
Metric Prefixes
Mega
kilo
deci
centi
milli
micro
nano
pico
femto
Length
Force
Volume
M
k
d
c
m

n
p
f
“million”
“thousand”
“tenth”
“hundredth”
“thousandth”
“millionth”
“billionth”
“trillionth”
“quadrillionth”
1 in = 2.54 cm
1 ft = 30.48 cm = .3048 m
1 yd = 91.44 cm = .9144 m
1 mi = 1609 m
1 pound = 4.45 newtons
1 ton = 8896 newtons
1 liter = 1000 ml = 1000 cm3
1 liter = 1.0576 quarts
1 gallon = 4 quarts
1 gallon = 3.79 liters
1 m3 = 1000 liters
9
1,000,000
1,000
.1
.01
.001
.000 001
.000 000 001
.000 000 000 001
.000 000 000 000 001
106
103
10-1
10-2
10-3
10-6
10-9
10-12
10-15
J. Trigonometry and Geometry
Sine, cosine and tangent functions are essential in the study of physics in two dimensions. Read
through the examples and complete all practice problems.
What do Sine, Cosine and Tangent mean?
Sin  
opposite
hypotenuse
SOH
adjacent
Cos  
hypotenuse
Tan  
opposite Sin 

adjacent Cos 
hypotenuse
(hyp)
CAH
opposite
(opp)

TOA
adjacent
(adj)
Pythagorean Theorem:
adj 2  opp 2  hyp 2
24. Using your calculator to evaluate the functions, complete the following table. Make sure your
calculator is set in degree mode (not radian mode).
θ = 30º
θ = 60º
θ = 45º
Sin 30º =
Sin 60º =
Sin 45º =
Cos 30º =
Cos 60º =
Cos 45º =
Tan 30º =
Tan 60º =
Tan 45º =
Using Sin, Cos and Tan to find the sides or angles of a triangle.
Example 1:
opp
20
opp  20 sin 30
sin 30 
opp  20 * 0.5  10
20
adj
cos 30 
20
adj  20 cos 30
adj  20 *
opp
30º
3
 10 * 3  17.3
2
adj
10
Example 2:
12
18
 12 
  sin 1    42 
 18 
sin  
18
12
12
adj
12
adj 
 13.4
tan 42
OR
tan 42 

adj
adj 2  12 2  18 2
adj  18 2  12 2  13.4
Solve for the unknown side lengths (x, y, and/or z) and angles (θ) in the following triangles. Show
your work. Write the answers on the line for that question on the answer sheet.
25.
26.
27.
6
z
9
y
5

y
60º
45º
x
8
28.
4.5
29.
30.
z
z
6.5
35º
3.6
y
2.3

1.8
x
11
18º
x
Answer Sheet – Physics Summer Work
1. (i)_________
(ii)_________
(iii)_________
(iv)_________
9. ____________
10.____________
11. (i)_________
24. _____ ______ _____
_____ ______ _____
_____ ______ _____
(ii)_________
2. (i)_________
(ii)_________
(iii)_________
(iv)_________
3. ____________
4. ____________
5. (i)_________
(ii)_________
(iii)_________
(iv)_________
(v)_________
(vi)_________
6. (i)_________
(ii)_________
(iii)_________
7. ____________
25. z =______ θ =______
12. (i)_________
(ii)_________
26. x =______ y =______
27. y = _________
13. (i)_________
(ii)_________
28. z =______ θ =______
29. x =______ z =______
14. ____________
15. ____________
16. ____________
17. ____________
18. ____________
19. ____________
20. ____________
21. ____________
22. ____________
23. ____________
8. ___________
12
30. x =______ y =______
13