* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Unit 3 Notes
Duality (projective geometry) wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Contour line wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Euler angles wikipedia , lookup
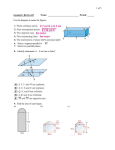
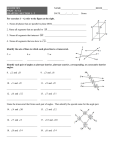
Chapter 3 Name ________________________ Geometry Block 3.1 identify Pairs of Lines and Angles Vocabulary: Parallel lines – two lines that do not intersect and are coplanar. The symbol // means “is parallel to.” Perpendicular lines – two lines that intersect to form a right angle. Skew lines – two lines that do not intersect and are not coplanar. Parallel planes – two planes that do not intersect. A transversal is a line that intersects two or more coplanar lines at different points. 3.1 identify Pairs of Lines and Angles Lines m and n are parallel lines . Symbol: m ǁ n k n T Lines m and k are skew lines. m U Lines k and n are intersecting lines, And there is a plane (not shown) containing them. Planes T and U are parallel planes. Symbol: T ǁ U Example 1 Identify relationships in space Think of each segment in the figure as part of a line. Which line(s) or plane(s) in the figure appear to fit the description? 1) Line(s) parallel to 𝐶𝐷 and containing point A. 2) Lines(s) skew to 𝐶𝐷 and containing point A. 3) Line(s) perpendicular to 𝐶𝐷 and containing point A. 4) Plane(s) parallel to plane EFG and containing point A. Parallel and Perpendicular Lines Parallel Postulate P • If there is a line and a point not on the line, then there is exactly one line through the Point parallel to the given line. l There is exactly one line through P parallel to l Perpendicular Postulate If there is a line and a point not on the line, Then there is exactly one line through the Point perpendicular to the given line. There is exactly one line through P perpendicular to l. P• l Example 2 Identify parallel and perpendicular lines Photography The given line markings show how the roads are related to one another. Angles and Transversals Corresponding angles - have corresponding positions on the lines and the transversal. Alternate Interior angles - lie between the two lines and opposite sides of the transversal. Consecutive Interior angles - lie between the two lines and on the same side of the transversals. Alternate Exterior angles - lie outside the two lines and opposite sides of the transversal. Example 3 Identify angle relationships Identify all pairs of angles of the given type. 1) Corresponding 2) Alternate Interior 3) Alternate Exterior 4) Consecutive Interior SOLUTION 3.2 Use Parallel Lines and Transversals Corresponding Angles Postulate If two parallel lines are cut by a transversal, then the pairs of corresponding angles are ≅. Alternate Interior Angles Theorem If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are ≅. Alternate Exterior Angles Theorem If two parallel lines are cut by a transversal, then the pairs alternate exterior angles are ≅. Consecutive Interior Angles Theorem If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are complementary (equal to 180⁰). Example 1 Identify congruent angles The measure of three of the numbered angles is 120°. Identify the angles. Explain your reasoning. SOLUTION Example 2 Use properties of parallel lines ALGEBRA SOLUTION Find the value of x. Example 3 Prove the Alternate Interior Angles Theorem Prove that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. SOLUTION Example 4 Solve real-world problem Science When sunlight enters a drop of rain, different colors of light leave the drop at different angles. This process is what makes a 0 rainbow. For violet light, m2 40 . What is m1 ? How do you know? 3.4 Prove Lines are Parallel How can you Prove that Lines are Parallel? Corresponding Angles Converse: If two lines are cut by a transversal so the corresponding angles are congruent (≅), then the lines are parallel. Examples: Find the value of x that will make line u and v parallel. a) b) Example 1 Prove that if two lines are cut by a transversal so the corresponding angles are congruent, then the lines are parallel. SOLUTION GIVEN : PROVE : 4 5 g h Alternate Interior Angles Converse: If two lines are cut by a transversal so the alternate interior angles are congruent (≅), then the lines are parallel. 2 6 Examples: Find the value of x that will make line u and v parallel. a) b) Example 2 Prove the Alternate Interior Angles Converse In the figure, Prove: p ⃦q SOLUTION 𝒓 ⃦𝒔 and 1 3 Alternate Exterior Angles Converse: If two lines are cut by a transversal so the alternate exterior angles are congruent (≅), then the lines are parallel. Examples: Find the value of x that will make line u and v parallel. a) b) Example 3 Prove the Alternate Exterior Angles Converse In the figure, 𝒓 ⃦𝒔 and 1 16 . Prove: r s p 1 p ⃦q q 8 16 Consecutive Interior Angles Converse: If two lines are cut by a transversal so the consecutive interior angles are supplementary (1800), then the lines are parallel. Examples: Find the value of x that will make line u and v parallel. a) b) Example 4 Prove the Consecutive Interior Angles Converse In the figure, 𝒓 ⃦𝒔 and 6 10 . Prove: r s 10 p ⃦q 4 6 12 p q Transitive Property of Parallel Lines p If two lines are parallel to the same line, then they are parallel to each other. q r If 𝑝 ⃦ 𝑞 and 𝑞 ⃦ 𝑟 , then 𝑝 ⃦ 𝑟. Example: U.S. Flag The flag of the United States has 13 alternating red and white stripes. Each stripe is parallel to the stripe immediately below it. Explain why the top stripe is parallel to the bottom stripe. 3.4 Find and Use Slopes of Lines Key Concepts: Slope the ratio of vertical change (rise) to horizontal change (run) between any two points on the line ‘m’ (lower case m) is the symbol used to represent the slope Change in y or y Rise y y1 m m 2 Change in x or x Run x2 x1 Negative slope falls from the left to the right Positive slope rises from left to right Zero slope (m = 0) horizontal (line) Undefined slope vertical (line) Example 1 Find slopes of lines in coordinate plane Find the slope of line a and line d. Solution Picture this! Two parallel lines never intersect. The slopes (𝑟𝑖𝑠𝑒) (𝑟𝑢𝑛) of these two lines are the same. 𝒎𝟏 = 𝒎𝟐 Two perpendicular lines form a right angle. The slopes of these two lines are exact opposite reciprocals of each other (the product of their slopes is -1.) 𝒎𝟏 ∗ 𝒎𝟐 = −1 Example 2 Identify parallel lines Find the slope of each line. Which lines are parallel? Example 3 Graphing Line h passes through (3, 0) and (7, 6). Graph the line perpendicular to h that passes through the point (2, 5). Solution 3.5 Write and Graph Equations of Lines Slope-intercept form of a linear equation is 𝒚 = 𝒎𝒙 + 𝒃 𝒎 = slope 𝒃 = y-intercept Rewrite the following equations in slope-intercept form. 1) 4𝑥 + 𝑦 = −8 2) 11𝑥 + 7𝑦 = −21 Example 1 Write an equation of a line from a graph Write an equation of the line in slope-intercept form. a) b) How to write an equation of a parallel line Write an equation of the line passing through the point (4, 4) that 9 is parallel to the given line with the equation 𝑦 = 𝑥 − 1 . 2 Steps: Determine the slope of the given line. m = ______ Determine the slope of the parallel line. m = ______ Plug in the given information (4, 4) into the slope-intercept form. x = ___ and y = ____ y = mx + b______________ Solve for the y-intercept of the desired equation. Write the equation in slope-intercept form: _________________ Example 2 Write an equation of a parallel line 3 1) Given line equation: 𝑦 = − 2 𝑥 + 4 ; passing through point (2, 1). 2) Given line equation: 𝑦 = −2 𝑥 − 2 ; passing through point (0, -3). How to write an equation of a perpendicular line Write the slope-intercept form of the equation of the line that is 1 perpendicular to the line 𝑦 = 𝑥 + 3 and contains the point (-2, 4). 4 Steps: Determine the slope of the given line. m = ________ Determine the slope of the perpendicular line. m = _______ Plug in the information into the slope-intercept form. x = ____ and y = ____ y = mx + b____________ Solve for the y-intercept of the desired equation. Write the equation in slope-intercept form: ______________ Example 3 Write an equation of a perpendicular line 1 1) Given line equation: 𝑦 = − 4 𝑥 + 1 ; passing through point (1, 5). 1 2) Given line equation: 𝑦 = 3 𝑥 − 3; passing through point (-2, 5). 3.6 Distance from a Line The distance from a point to a line is the length of the perpendicular segment from the point to the line. This perpendicular segment is the shortest distance between the point and the line. C A k D E F > > m p B Distance between two parallel lines. Distance from a point to a line. Example 1 Find the distance between two parallel lines. Example 2