* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Computer Games - CSE, IIT Bombay
Fortress (chess) wikipedia , lookup
Draw by agreement wikipedia , lookup
Chicken (game) wikipedia , lookup
Chess opening wikipedia , lookup
Shogi strategy wikipedia , lookup
First-move advantage in chess wikipedia , lookup
Promotion (chess) wikipedia , lookup
Artificial intelligence in video games wikipedia , lookup
Chess strategy wikipedia , lookup
Endgame tablebase wikipedia , lookup
Chess theory wikipedia , lookup
Computer chess wikipedia , lookup
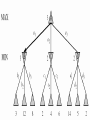
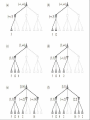
Group 1 : Ashutosh Pushkar Ameya Sudhir From CHECK TO CHECKMATE ! Motivation Game playing was one of the first tasks undertaken in AI Study of games brings us closer to : Machines capable of logical deduction Machines for making strategic decisions Analyze the limitations of machines to human thought process Games are an idealization of worlds World state is fully accessible Actions & outcomes are well-defined Outline of the presentation Evaluation Functions Algorithms Deep Blue Conclusions from Deep Blue Conclusion References Chess Neither too simple Nor too difficult for satisfactory solution Requires “thinking” for a skilled player Designing a chess playing program Perfect chess playing : INTRACTABLE Legal Chess : TRIVIAL Play tolerably good game : SKILLFULLY Evaluation Function Evaluation Function Utility function Whole game tree is explored computationally expensive task !! Estimates the expected utility of a state Evaluation functions cut off the exploration depth by estimating whether a state will lead to a win or loss Evaluation Function (cont.) A good evaluation function should not take too long Preserve ordering of the terminal states otherwise it will lead to bad decision making Consider strategic moves that lead to long term advantages Evaluation Function (cont.) Typically includes : Material Advantage (difference in total material of both sides) f (P) = 200(k – k’) + 9(q – q’) + 5(r – r’) + 3(b – b’) + (p – p’) + g(P) + h(P) +… Positions of pieces Rook on open file double rooks rook on seventh rank etc. and their relative positions. Pawn Formation Mobility Evaluation function is an attempt to write a mathematical formula for intelligence Algorithms Games as Search Problems Initial states Where game starts Initial position in chess Successor function List of all legal moves from current position Terminal State Where the game is concluded Utility function Numeric value for all terminal states Minimax Strategy Minimax Strategy Optimal strategy Assumption : opponent plays his best possible move. An option is picked which Minimizes damage done by opponent Does most damage to the opponent Idea: For each node find minimum minimax value Choose the node with maximum of such values This will ensure best value against most damage done by opponent Strategy of Minimax Opponent tries to reduce utility function’s value For any move made by opponent in reply of computer’s move, choose minimum reduced value by opponent Find the move with maximum such value Analysis Algorithm is complete for complete tree only Not best strategy against irrational opponent According to definition Time complexity :O(bm) b = max. no. of possible moves m = max. depth of tree In chess even in average case, b = 35 and m = 100 => time exceeds practical limits # of states grows exponentially as per number of moves played α-β Pruning α-β Pruning The problem of minimax search # of state to examine: exponential in number of moves Returns same moves as minimax does Prunes away branches that can’t influence final decision. α: the value of the best (highest) choice so far in search of MAX β: the value of the best (lowest) choice so far in search of MIN Order of considering successor Algorithm for α-β Pruning Current highest β is found and assigned as α β is current lowest for α’s from that move For next possible node, while finding β, if some α is found lower than current highest β: It will only give lesser value of final β S0, other α’s are not found for that node After calculating β for this node, α is replaced by max(α,β for this node) In this way after all possible set of moves final value of α is found α-β Pruning (2) If m is better than n for Player, we will never get to n in play and just prune it. Analysis of α-β Pruning: Improvement over minimax algorithm Does not affect final results Worthwhile to examine that successor first which is likely to be best Time complexity: O(b(m/2)) Effective branching factor = √b i.e. 6 rather than 35 In case of random ordering : Total number of nodes examined is of the order O(b^(3m/4)) Transposition table Dynamic programming Multiple paths to the same position Savings through memorization Use a hash table of evaluated positions Iterative Deepening Sometime chess is played under a strict time Depth of search depend on time Use of Breadth first Search Advantage : program know which move was best at previous level Horizon Effect Problem with fixed depth search Positive Horizon Effect Negative horizon effect Quiescence Search Search till “quiet” position Quiet Position Doesn’t affect the current position so much Example : no capture of any piece, no check, no pawn promotions/threats State of the art : DEEP BLUE Defeats Gary Kasparov Won a match in 1997 Brute force computing power Massive, parallel architecture Special purpose hardware for chess Parameters of the evaluation function Learnt by studying many master games Different evaluation function for different positions Utilized heavily loaded endgame databases Humans vs. Computers Humans Computers Lower Computational Speed Higher Errors Possible Error Free Tend to be instinctive No instincts Imaginative None High Learning Capabilities Limited Inductive Not Inductive Some intricacies of a chess playing system Should not play the same sequence of moves again A player wins a match against the computer Starts playing the same sequence of moves Hence, a statistical element is required Opponent can learn the algorithm used by computer Hence, again the need for a statistical element Different game play during different phases Start Game Mid Game End Game Conclusion Computer chess as a search problem Good enough decisions Simulation of “skill” by “knowledge” Limitations of computers to humans Future work : Better evaluation functions through learning Need for different AI techniques to play chess References Claude E. Shannon: Programming a Computer for Playing Chess, Philosophical Magazine, Ser.7, Vol. 41, No. 314, March 1950. S.Russel & P. Norvig: Artificial Intelligence: A Modern Approach 2/E, Prentice Hall, ISBN-10: 0137903952 Wikipedia Thank You