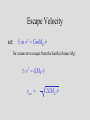Download Orbital Paths

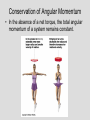
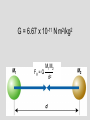
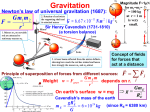
Who cares about momentum (mv)?
Conservation of linear Momentum
• In the absence of a net force, the total linear
momentum of a system remains constant.
But this is just Newton’s first law!!
mv = constant
Conservation of Angular Momentum
• In the absence of a net torque, the total angular
momentum of a system remains constant.
Universal Law of Gravitation
Between every two objects there is an attractive
force, the magnitude of which is directly
proportional to the mass of each object and
inversely proportional to the square of the
distance between the centers of the objects.
Fg a
M1M2
d2
G = 6.67 x 10-11 N m2/kg2
Fg = G
M1M2
d2
F=
G
circumference =
m m
1
2
2pR
R2
R
m1
m2
v = distance / time
v = 2pR / P
2
F = m1a = m1 v / R =
G
m1 m2
R2
v2 = G m2/R
4p2 R 2 / P 2 = G m /R
2
4p2 R 3 = G m P 2
P2 = (4p2/Gm2) R3
2
• Gravitational Potential Energy for the surface of
the Earth is:
mgr (where r is the radius of the Earth)
F = ma
= mg
= GmME/r2 = m (GME /r2)
so:
and:
g = GME /r2
mgr = m(GME /r2) r
So, Gravitational Potential Energy = m(GME /r)
Escape Velocity
set: ½ m v2 = GmME /r
for a mass m to escape from the Earth (of mass ME)
½ v2 = GME /r
vesc =
2GME /r
Orbital Paths
• Extending Kepler’s
Law #1, Newton
found that ellipses
were not the only
orbital paths.
• possible orbital
paths
– ellipse (bound)
– parabola (unbound)
– hyperbola (unbound)
Changing Orbits
orbital energy = kinetic energy +
gravitational potential energy
conservation of energy implies:
orbits can’t change spontaneously
An object can’t crash into a planet
unless its orbit takes it there.
An orbit can only change if it
gains/loses energy from another
object, such as a gravitational
encounter:
If an object gains enough energy so that its new orbit is unbound,
it has reached it’s escape velocity.
How do we do astronomy?
We look at stuff
We collect stuff that travels to us from far away – matter and
radiation – this is what we mean by “look”
What is light?
Four Ways in Which Light can Interact
with Matter
emission
absorption
transmission
reflection
But, what is light?
• In the 17th Century, Isaac Newton argued
that light was composed of little particles
while Christian Huygens suggested that light
travels in the form of waves.
• In the 19th Century, Thomas Young
demonstrated that light bends slightly around
corners and acts like interfering waves.
Light
A vibration in an electromagnetic field
through which energy is transported.
Light as a wave
f=c
Light as a particle
E=
a hf
f
photon
Planck’s constant h = 6.6 x 10-34 J s
Scottish physicist James Clerk Maxwell showed
mathematically in the 1860s that light must be
a combination of electric and magnetic fields.