* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Magnetic Interaction
Magnetosphere of Jupiter wikipedia , lookup
Magnetosphere of Saturn wikipedia , lookup
Geomagnetic storm wikipedia , lookup
Skin effect wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
Electromotive force wikipedia , lookup
Edward Sabine wikipedia , lookup
Maxwell's equations wikipedia , lookup
Superconducting magnet wikipedia , lookup
Magnetic stripe card wikipedia , lookup
Electromagnetism wikipedia , lookup
Magnetic field wikipedia , lookup
Mathematical descriptions of the electromagnetic field wikipedia , lookup
Giant magnetoresistance wikipedia , lookup
Magnetometer wikipedia , lookup
Magnetic nanoparticles wikipedia , lookup
Earth's magnetic field wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Magnetic monopole wikipedia , lookup
Electromagnetic field wikipedia , lookup
Magnetotactic bacteria wikipedia , lookup
Lorentz force wikipedia , lookup
Magnetotellurics wikipedia , lookup
Multiferroics wikipedia , lookup
Force between magnets wikipedia , lookup
Electromagnet wikipedia , lookup
Magnetoreception wikipedia , lookup
History of geomagnetism wikipedia , lookup
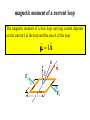
magnetic interaction There is interaction between a particle and other bodies which depends on the charge of the particle, its position and its velocity (and its spin). We call this interaction a magnetic interaction. Moving charged particles in the body cause the magnetic interaction. B ++ v F O The region of space in which magnetic forces can be exerted is called a magnetic field. magnetic field vector The magnetic field vector B at position r is a vector such that, at this position, the magnetic force exerted on a particle with charge q, moving with velocity v, would be FB qv B B F ++ v the cyclotron frequency FB q qB a v v B m m m Recall that in a uniform circular motion: a = v B ++ v F O In a uniform magnetic field, the particle moves with constant angular velocity along the magnetic field qB m work due to magnetic interaction ds + v F dWB FB d s FB vdt 0 B The magnetic work performed on the particle is zero. (A magnetic field cannot change the speed of a particle.) magnetic force "on a current" B Ids dF I The (differential) force dF, exerted on a (differential) segment, depends on the current I in the wire, the size ds and orientation ŝ of the segment, and the magnetic field vector B at the location of the segment: dF Id s B dF qvdsˆ B nAds nvdq A ds B Id s B magnetic moment The magnetic moment of an object is a vector such that the magnetic torque exerted on the object (about its center of the mass) placed in the magnetic field B is B Puzzle. What is the direction of the magnetic moment of a compass needle? B N B B S B magnetic moment of a current loop The magnetic moment of a wire loop carrying current depends loop. a and the area a A of the current Iin the loop on the 1 2 3 4 Ib nˆ B Ib nˆ B 0 0 IA B 2 2 IA n̂ F1 b B a F2 potential energy The potential energy of an object in a magnetic field depends on the magnetic moment of the object and the magnetic field at its location U B S N S N The Lorentz force When the particle moves in the presence of both a magnetic field and an electric field, the net force depends on both fields: F qE qv B Example. The Hall effect V qvd B qEH VH E H d v d Bd d VH IB nqA + + + + + + + FB d vd + _ FE _ _ _ I _ _ _ Maxwell's equations . . . and God said: Let . . . Q E dA 0 Gaussian Surface d B E ds dt Amperian Loop B dA 0 Gaussian Surface d E B d s I 0 0 dt Amperian Loop . . . and there was light. Gauss‘s law for magnetic fields The net electric flux through any The net magnetic flux through closed (Gaussian) surface is any closed (Gaussian) surface proportional to the net charge is equal to zero: inside the surface: B dA q0in E dA Gausian 0 SSurface N Faraday's law of induction N B E The line integral of the electric field vector around any closed path equals the rate of change in the magnetic flux through any surface bounded by that path. d B E d s dt closed loop Ampere-Maxwell law E E B I The circulation of the magnetic field vector around any amperian loop proportional the sum of the total conduction current and the displacement current through any surface bounded by that path. d E B ds 0 I 0 dt closed loop The proportionality coefficient is called the permeability of free space. displacement current The rate of change in the electric field multiplied by the permittivity of free space is called the displacement current dE Id 0 dt I Example: Q E -Q I Id 0 d E dt Q d 0 dQ 0 I dt dt Example: Magnetic field of a long straight wire with current I v ds B 0I B 2 R + R F 2 R 2 R 0 I B d s Bds B ds 2R B loop 0 0 the Biot-Savart law dB Ids 0 Ids r dB 4 r2 P r I The (differential) magnetic field at a certain position P produced by a differential element carrying electric current I depends on the value of the current and the size and orientation of the segment. Example: infinite straight wire with current I 0 Id s rˆ dB y 2 4 r z y dB x R P r s Ids B B y 0 IR 4 - R s 2 3 2 0 I sin ds 2 4 r 0I 1 R 2 2 ds 2 2 4 R s R s ds 2 0 IR 4 R ds 2 s 0 s IR 4 R 2 R 2 s2 2 3 2 0I 2R Interaction between two parallel current B1 F21 I1 I2 a 1 2 0 l F21 I2 l B1 I2 I1 aˆ 2a 0 l I2 aˆ I1 I1 I2 aˆ 2a 0 l I1 I2 aˆ 2a l The magnitude of the magnetic force exerted on segment l of a wire by the other wire (infinite) is 0l F21 I1I2 2a Parallel "currents" attract and antiparallel repel. magnetic field of a solenoid The magnetic field outside the solenoid is zero Bout 0 The magnetic field inside is uniform, its direction is parallel to the axis, and the magnitude depends on the current and the number of loops per length of the solenoid Bin 0nI N S L I I Magnetic properties of matter When a substance is placed in a (external) magnetic field, its molecules acquire a magnetic moment related to the external field. This creates an additional magnetic field (internal). B B 0 Bm 1 B 0 B0 paramagnetics: > 1 Bm diamagnetics: <1