* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 幻灯片 1
Ultraviolet–visible spectroscopy wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Franck–Condon principle wikipedia , lookup
Gaseous detection device wikipedia , lookup
Auger electron spectroscopy wikipedia , lookup
Photomultiplier wikipedia , lookup
Photonic laser thruster wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Nonlinear optics wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Upconverting nanoparticles wikipedia , lookup
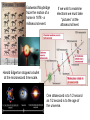
In 1909 G.I. Taylor experimented with a
very dim light source. His work, and
many modern experiments show that
even though only one photon passes
through a double slit, over time, an
interference pattern is still produced one “particle” at a time.
=h/p
“It would seem that the basic
idea of the quantum theory
is the impossibility of
imagining an isolated
quantity of energy without
associating with it a certain
frequency.”
Louis de Broglie, in
1923, reasoned that if
light waves could
behave like particles
then particles should
have a wavelength.
n=2dsin
Soon after, an experiment by C. J. Davisson and
L. H. Germer showed that electrons could produce
interference patterns just like those produced by light.
De Broglie’s
• G.I. Taylor, one of the most distinguished physical scientists of
this century, used his deep insight and originality to increase our
understanding of phenomena such as the turbulent flow of fluids.
His interest in the science of fluid flow was not confined to theory;
he was one of the early pioneers of aeronautics, and designed a
new type of anchor that was inspired by his passion for sailing.
His experiment with photons resulted in his first paper. It leads
us to understand that even though one photon encounters the
double slits, wave properties still appear, but are displayed in a
particle fashion.
• Prince Louis De Broglie’s proposed the idea that
particles can also be thought of as waves for his PhD
thesis. It was a difficult sale and required the
intervention of Einstein.
Heisenberg’s Uncertainty Principle
helps us examine the dual nature of
light, electrons, and other particles.
p=/h
If we add
together many
wavelengths...
{
If we know the wavelength we
are certain about the momentum.
But, because a wave is spread
out in space, we are uncertain
about its position.
{
We are uncertain
about the
momentum.
But, we are now
more certain
about position.
Particle or Wave?
• So what is light, particle or wave? Heisenberg’s
idea lets us think about a particle as a sum of
waves. The more you know about the particle
properties, because it is a sum of waves, the
less you know about its waviness and visa versa.
It is sometimes instructive to have students add
waves using a graphing calculator or computer
graphing program. I often do this first when
talking about beats in my unit on sound.
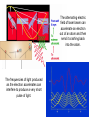
Heisenberg Uncertainty
• This can be discussed in terms of the Heisenberg Uncertainty
principle. If you don’t know the actual location of the photons they
produce wave behavior but as soon as you know the location (one
slit or the other) the particle properties appear and the interference
pattern disappears.
• In the second set of diagrams each red lines represent one photon
that arrives at a photo-detector. In the top diagram it is set up so
that the waves destructively interfere for the top detector and
constructively interfere for the bottom. In the lower diagram on the
right, because you know which path the photon has followed it
behaves like a particle and follows one of the two paths. Thus, you
can tell if someone is eves dropping on the system by the output of
the system.
Potential Energy
Potential energy for a classical
harmonic oscillator is continuous
and can have a value of zero.
Position
Schrödinger's equation was
published in 1926. The solution of
this equation for a particular
particle and the forces acting on
that particle is called the wave
function ().
Quantized
energy levels
Zero-point
energy
Maxwell showed that oscillating
electric charge produces an
electromagnetic wave.
Unlike the classic oscillator, this
system has a minimum energy or
“zero-point” energy.
Schrödinger Equation
• More quantum strangeness comes when we consider an harmonic
oscillator. If you think of a spring in a classical sense, it can have
zero spring potential energy when it stops vibrating.
• Erwin Schrödinger, in a attempt to explain the waves associated
with the electron, developed his wave equation. Given the mass of
the particle, and the forces to which it is subjected - the spring for
the harmonic oscillator - Schrödinger's equation gives us all the
associated waves and in turn, the possible energies. Applying the
equation to the harmonic oscillator we find that there is a lowest
possible energy or zero-point energy and that the system can’t go
below that energy.
Schroedinger’s Equation
(continued)
•
Schroedinger: If electrons are
waves, their postion and motion in
space must obey a wave equation.
•
Solutions of wave equations yield
wavefunctions, Y, which contain
the information required to
describe ALL of the properties of
the wave.
•
Provides a picture of the electronic
distributions of the electrons about
an the nucleus of an atom and
about the connected nuclei of a
molecule.
Schrödinger’s Improvement
to Bohr’s Model
• Showed how to obtain Bohr’s formula using the
Schrödinger equation
• Electron is described by a wave function y
• Solved for y in the electric potential due to the
nucleus of the hydrogen atom
Quantum Square Well
• Approximate electric (roller coaster)
potential by a ‘square well’
• System is then identical to the wave
equation for a string that is fixed at both
ends
Summary
• Electron does not fly round the nucleus
like the Earth around the Sun (Rutherford,
Bohr)
• Depending on which energy level it is in,
the electron can take one of a number of
stationary probability
cloud configurations (Schrödinger)
Energy Levels in a Box
Atoms and molecules can also absorb photons,
making a transition from a lower level to a
more excited one
Excited level
Energy
This photon has
been absorbed
Ground level
In 1916, Einstein showed that another process,
stimulated emission, can occur
Before
Spontaneous
emission
Absorption
Stimulated
emission
After
Stimulated emission
A vibrating rope
between two fixed
points can only
produce standing
waves that are a
multiple of 1/2 .
Because of the zero point energy
even a complete vacuum is filled with
waves of every wavelength…
but only certain wavelengths can exist
between two closely spaced mirrors in
the vacuum.
F = πhc/480 d4
In 1948 Hendrick Casimir
predicted that these two
mirrors would be pushed
together because of the
difference in energy.
Once you have
designed optics to
correct for aberrations
caused by the
lenses…
diffraction still limits the
size of objects we can
resolve. The smaller
the object
the shorter
the wavelength
required.
Diffraction
• We can apply what we know about light to help us build a better
microscope. Chromic and spherical aberrations have been corrected
in modern lens with coatings and combinations of lenses made out
of materials with different indexes of refraction.
• After making those corrections you still need to deal with diffraction.
Because of light’s wave nature there is a limit to what an optical
microscope can resolve.
• Ernst Abbe found that the limit for resolving an object because of
diffraction was described by the formula shown above.
• A modern microscope, like the one pictured that uses fluorescence
(see next slide), can not overcome this limit.
Using Schrödinger's wave
equation, can be
calculated for electrons
in the Coulomb
potential of
an atom.
These calculations show
discrete energy levels similar to
the calculations for a harmonic
oscillator.
An electron is
excited to a
higher energy
when a photon is
absorbed and
gives off a photon
when it relaxes to
a lower energy.
gives us the
probability of
finding an
electron in a
particular
location.
An atom
fluoresces
when a short
photon
excites the
atom and a
longer
photon is
given off.
Probability Spaces
•
•
•
To understand how fluorescence can be used to enhance an image we
need to discuss the structure of an atom. Schrödinger's wave equation is
used to describe the possible electron waves that can exist inside the
Coulomb field of the atom, not unlike the allowed vibrations for an harmonic
oscillator. Each allowed wave represents a different energy level the
electron can occupy. In a hydrogen atom, as in any atom, the electron
jumps between those levels give rise to the spectrum for that atom.
Because of Heisenberg's Uncertainty relationship we can’t know exactly
where the electron will be but the square of the wave function tells us the
probability of finding an electron in a particular location in the atom. These
are probability spaces are the orbitals we have come to know from
chemistry.
In a fluorescent molecule a photon my excite an electron to a higher energy
level, that electron relaxes to a slightly lower level, then drops back to the
ground state giving off a lower energy photon. The color of the emitted light
is characteristic of the substance fluorescing.
Energy is “pumped” into the
medium, exciting electrons to the
metastable state.
An electron drops to the
Meta-stable state
ground state and
produces a photon.
That photon interacts with
another excited electron
causing it to drop.
Coherent
Collimated
Monochromatic
Ground state
A second photon is produced
by stimulated emission.
Those photons reflect and continue
to stimulate more photons.
Laser and Einstein
•
•
•
•
Another development important to modern microscopes is the laser. Some
energy levels inside the atom are metastable. Normally the average life
time of an excited atom is about 10-8 s. In a metastable state the electrons
may remain excited for 105 times longer before spontaneously emitting a
photon. This allows time to get many atoms into a metastable state and
create a population inversion where there are more excited atoms than
ground state atoms.
In 1917 Einstein introduced the concept of stimulated emission, meaning
that a photon can stimulate another atom to emitt an identical photon.
“Laser” is an acronym for” light amplification by the stimulated emission of
radiation”.
There is a mirror at each end of the laser. One mirror is close to 100%
reflective, and the other allows a small amount of light to escape. As the
photons bounce back and forth between the mirrors they are “amplified” by
causing stimulated emissions from other atoms.
Because of this process, all the photons in the light emitted have the same
energy, phase, polarization, and direction of travel.
If you have a very
intense light, two
photons can induce a
single fluorescence.
In single photon
excitation, fluorescence
is produced all along
the path of the light.
In two-photon
excitation the light is
only intense enough to
produce fluorescence
at the focal point.
Confocal Microscope
• To improve the confocal microscope two-photon excitation is used.
A laser is pulsed to provide a very intense beam of light with many
photons. The photon energy is half the energy needed to excite the
fluorescent molecule so two photons are needed to do the excitation.
This can only happen because of the intensity of the beam.
• A disadvantage to the confocal microscope is the fact that the light
tends to be dispersed as it travels through the object. This makes it
hard to see deeper layers. Fluorescent markers also tend to “bleach”
or fade under illumination. The two-photon method eliminates that
problem because the beam is only intense enough to get excitation
at the focal point so no other molecules fluoresce. This also
eliminates the need for the pinhole because light only comes from
the one point. Scanning gives you images such as these neurons.
Can we break the
diffraction limit?
Because of
diffraction a
molecule
might look
like this.
But we would have a
pretty good idea of
its location.
If we have many
molecules in the
same location we
will not be able to
resolve them…
unless we can turn them
on one molecule at a
time.
Diffraction Limit
•
•
•
To break the diffraction limit described by Abbe we must go one step further.
Diffraction will make a molecule look blurred out. Even so, we have a good
idea where the molecule is. If you have many molecules in one small area
it will be difficult to locate individual molecules.
Chemical compounds have been developed that can be turned on and off.
A laser activates them, giving them the ability to fluoresce. These
molecules are attached to the structure of interest, are activated and then
when excited tell us the location of that structure. The trick is to illuminate
the sample with a very weak excitation beam so that only a few photons
strike the sample at a time. In this way only one molecule fluoresces at a
time and its location can be inferred. These marker bleach out quickly,
turning the fluorescence off again.
Using this technique we can use visible light to see things smaller then the
typical 2 µm diffraction limit for visible light. In these pictures we see fibers
in a sample, first with a conventional microscope and then using this
process. Different structures can be seen by using different labeling
compounds.
Eadweard Muybridge
froze the motion of a
horse in 1878 - a
millisecond event.
If we wish to examine
electrons we must take
“pictures” at the
attosecond level.
Harold Edgerton stopped a bullet
at the microsecond time scale.
One attosecond is to 1/2 second
as 1/2 second is to the age of
the universe.
Ultra-fast Photos
• Light can also be put to work to help us look at events
that take place in very short time intervals. Muybridge
was motivated to take photos of a running horse to settle
the question of whether or not all four hoofs are off the
ground at the same time. Edgerton became famous for
his stop action photos, but if we wish to freeze the
motion of atomic or subatomic particles we need to deal
with attosecond flashes of light. It is fun to have
students work out their own comparisons for the size of
an attosecond.
The alternating electric
field of laser beam can
accelerate an electron
out of an atom and then
send it crashing back
into the atom.
The frequencies of light produced
as the electron accelerates can
interfere to produce a very short
pulse of light.
Short Pulses
• One way to make these incredibly short pulses is to
“rock” an electron back and forth inside an atom. If we
are thinking of light as an electromagnetic wave, the
alternating electric field of an intense laser beam can
push an electron away from the nucleus and out of an
atom and then as the field reverses, send the electron
crashing back into the nucleus, much like a ball on a
see-saw. The accelerating electron will produce a new
electromagnetic wave. This wave will change frequency
depending on where the electron is in its oscillation.
• If done properly all of these wavelengths will add up to
make a very short pulse of light.
These pulses of light,
interfering with the
electron itself, can tell
you everything you can
know about the
electron’s wave function.
Now, movies of atoms moving and
bonds breaking are possible.
FS Chemistry
• These very short pulses of light can then
interfere with the wave that is the electron
and tell you all about the electron’s place
in an atom or molecule. If this is done
frame by frame movies of chemistry in
action will soon be possible.
飞秒频闪观测谱(1987)
(Eadweard Muybridge摄)。
激光化学与飞秒频闪(1999)
阿梅特 蔡维尔(Ahmed Zewil,1946-, 埃及)因他的飞秒化学工作,
成了1999年诺贝尔化学奖得主。他还得到了提名并成了Barack Obama
总统的总统科技顾问委员会理事会(PCAST)的成员。BengtNorden教
授在1999年瑞典皇家科学院的诺贝尔化学奖颁奖仪式上说:“飞秒化
学从根本上改变了我们观测化学反应的方法。围绕在过渡态周边一百
多年的迷雾清晰了,我们现在能直接研究分子中原子的实际运动。蔡
维尔教授,我赏试着解释您的前驱性的工作,如何基本上改变了我们
观测化学反应的方法。从受制于仅用一个隐喻的术语“过渡态”来描
述它们,现在我们能同时以时间和空间的图像来描述它们,它们再也
不是不可见的。”Zewail成功地利用了快速飞秒激光光谱技术,即观
察一个分子的原子在化学反应过程中如何移动。飞秒光谱,泵探针实
验“照片”(图23),当它们发生化学反应时,用超快激光作为“闪
光”。