Download ppt Review from Kahoot

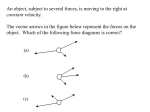
1. A 5 kg box slides on a frictionless incline. What
is the magnitude of its acceleration in m/s2?
FN
mgcosq
q
mg
tanq=3/4
q
a) 5
b) 6
B
c) 10
d) 30
Forces and accel: draw FBD, apply Newtons Laws
Fnet=Fgx = mgsinq
a=gsinq
2. Same box, same frictionless incline. What is the
magnitude of the normal force on the box?
a) 30 N
b) 40 N
B
c) 50 N
Tips: FN =Fgy = mgcosq
d) 60 N
3. If the box started from rest at the top, what is
its kinetic energy at the bottom?
a) 150 J
A
b) 250 J
c) 50 J
d) 60 J
Tips: asks about energy so apply conservation of energy to the problem
UgT= mgh= KB
4. The net work done on an object is always equal
to its change in:
a) Gravitational Potential Energy
b) Elastic Potential Energy
c) Kinetic Energy
d) Mechanical Energy
C
5. A 30 kg mass hangs still from a
spring with a k = 1500 N/m.
How much is the spring
stretched?
C
a) 0.002 m
c) 0.2 m
b) 0.02 m
d) 2 m
Fspr
Tip: draw FBD, block is at rest, all forces are
balanced Since block is at rest
Fspr = mg
kx = mg
x = mg/k
mg
6. The surface is frictionless. What is the tension
in the rope connecting the two boxes?
F
a) (2/5)F
D
b) (5/2)F
c) (2/7)F
d) (5/7)F
Tips: T is the net force on 5kg box which is 5/(2+5) F
System: asys = F/7
5kg box: Fnet=T=5a=5(F/7)
7. The surface is frictionless. What is the tension
in the rope connecting the two boxes?
a) (2/5)F
C
b) (5/2)F
c) (2/7)F
d) (5/7)F
Tips: T is the net force on 2kg box which is 2/(2+5) F
System: asys = F/7
2kg box: Fnet=T=2a=2(F/7)
8. The surface is frictionless. The acceleration of
the two masses is:
System
mg
a) g
b) g/2
C
c) g/3
d) 2g/3
Tips: asys = Fnet sys/Msys = mg/3m
9. The surface is frictionless. The tension in the
rope is:
FN
FT
2mg
a) 2mg/3
A
b) mg/2
c) mg/3
d) mg
Tips: FT is net force on 2m
Fnet 2 = FT = 2ma = 2mg/3 (2/3rds of Fnetsys)
10. The surface has friction. The masses don't
move. What's the minimum μs of the
surface/box? FN
FT
fs
FT
2mg
mg
a) 0.333
B
b) 0.5
c) 0.67
d) 2
Tips: Draw FBD, Net force on each block is 0
Fnet 2 = FT-fs = 0 and FT=mg
mg=ms(2mg)
11. A car slams its brakes and stops in a
distance d. Another car moving twice as fast...
a) d/2
D
b) d
c) 2d
d) 4d
Tips: want relationship between v0 and d, all else constant :
v2=v02+2ad (v = 0 and ax is same )
d=v02/2a (double v0 results in 4x d
OR W-E: Wnet=DK
-Fbraked = 0-1/2 mv02
d= mv02/(2Fd)
12. A car is parked on a level surface. The surface
exerts an upward normal force on the car.
a)
b)
c)
d)
The downward force of gravity on the car
The downward force of the car on the surface
The upward force the car exerts on the earth
The force of friction between the tires and the surface
B Tip: can write F
fully accounting for the pair of objects
involved in the interaction: FN, on car, by surface
Then the equal and opp force is FN, on suface, by car
N
13. The period of a satellite's orbit depends on...
C
a)
b)
c)
d)
I and II only
I, II, and III
I and III only
II and III only
Tips: the trajectory of a satellite DOES
NOT depend on the mass of the satellite.
Because a satellite is in free fall its
acceleration is mass-independent.
Orbital Motion: FG = FC and v=2pR/T
GMm/R2=mv2/R
GM/R= (2pR/T)2
T depends on M, mass of central planet
and R, the orbital radius
14. A planet has twice the radius of earth, and the
same density as earth.
a) 10 m/s2
c) 20 m/s2
b) 5 m/s2
d) 2.5 m/s2
C
Tips: express g in terms of density
g = GM/R2 = (4/3)pRr
where r = M/V .
Same density, 2x s R gives 2x g of Earth
15. A car moves clockwise around a circular track
(as viewed from above).
a) North
c) South
b) East
d) West
A
ac
v
16. A truck of mass m and a speed v passes the
top of a circular hill with a radius R.
FN
mg
B
Tip: FORCE so draw FBD
Car is moving in a curved
(circular) path, so there must be
a centripetal force. Apply
Newtons 2nd
FC =  Fr = mv 2 / R
mg  FN = mv 2 / R
a) mv2/R
c) (mv2/R)-mg
b) mg-(mv2/R)
d) mg+(mv2/R)
17. A mass m is supported by two ropes, as
shown. The rope on the left is horizontal.
T2sinq
T1
T2
T2cosq
mg
C
Tip: FORCES so draw FBD
m is in equilibrium: All forces
are balanced (Fnet = 0)
F
y
=0
T2 sin q  mg = 0
a) mgcosq
c) mg/sinq
b) mgsinq
d) mg/cosq
18. A ball of mass m is
tied to a string of
length L and
released with string
60o from vertical..
Lcos60
L
h=L-Lcos60
=0.5L
ET=EB
mgh=1/2mvB2
vB=(2g(0.5L)) = (gL)
a) (gL)
A
b) (2gL)
c) (gL/2)
d) (4gL)
Tip: In the absence of air resistance, a pendulum/Earth system
conserves mech E (T does no work, it is a centripetal force)
19. A box of mass m on a frictionless surface is
attached to a spring with a spring constant k.
Max velocity when all
the US is converted to K
(when the spring is at
relaxed, equilib position:
a) (dk/m)
b) d(k/m)
B
c) d(m/k)
Ei=Ef
1/2kd2=1/2mvf2
vf = d(k/m)
d) (k/dm)
Also only B has units of
velocity
Tip: Cant use kinematics with springs because the spring
force (and acceleration) is not constant. In the absence of
friction, the block/spring system conserves mech E
20. A car with a speed v brakes and skids to a stop.
The coefficient of kinetic friction is μ.
a) 2v2/(mg)
D
b) v2/(mg) c) 2mg/v2
d) v2/(2mg)
Tips: can eliminate C based on wrong units. consider EITHER
Forces (draw FBD and apply Newtons 2nd, use kinematics)
OR Work-Energy (Ei + WNC = Ef) (car/Earth is not isolated, Wf removes mech E)
FN
v
fk
mg
F
= ma x
x
 f k = ma x
 mmg = ma
a =  mg
OR
v f = v0  2a x d
2
2
d = v0 /(2a ) = v 2 /(2 mg )
2
Ei  W f = E f
1
2
mv 2  f k d = 0
1
2
mv 2  mmgd = 0
d = v 2 /(2 mg )
21. A truck of mass m and a speed v passes the
top of a circular hill with a radius R.
C
mg
Tip: only C and D have the
correct units
Car is moving in a curved (circular)
path, so there must be a
centripetal force. Draw FBD.
Apply Newtons 2nd. Truck looses
contact when FN = 0
FC =  Fr = mv 2 / R
mg = mv 2 / R
v = gR
a) gR2
b) gR
c) (gR)
d) (2gR)
22. The graph below shows the net force that acted
on a mass over a displacement of 8.0 meters.
Fav = 5N
a) 40 J
b) 24 J
Fav = 6N
c) 44 J
C
d) 66 J
Tip: Work
is area
under F-d
curve or
Favd for
each linear
region
23. The graph below shows the net force that acted
on a mass over a displacement of 8.0 meters.
B
Tip: Wnet=DK
Wnet=DK
44 = Kf-Ki
22=1/2mvf2
vf=2m/s
a) 1 m/s
b) 2 m/s
c) 3 m/s
d) 4 m/s
24. Why can a car travel with a greater speed w/o
slipping on a banked curve than on level
ground?
a)
b)
c)
d)
The force of friction is greater on the banked track.
Gravity helps supply centripetal force.
Normal force increases on the banked track.
The normal force helps supply centripetal force.
D
25. Which graph shows the relationship between
gravitational potential energy and height?
A
Ug=mgh
26. A ball thrown straight up with a
speed v reaches a maximum height h.
a) 2h
D
b) 4h
c) 8h
d) 16h
Tips: want relationship between h and v0 , all else constant :
Kinematics: vfy2=v0y2+2ayh (vfy = 0 at peak and ay is same )
h=v02/2g (4x v0 results in 16x h)
OR Conservation of Mech E
EB=ET
1/2mv02=mgh
h=v02/2g
27. A ball is thrown straight up with an initial
kinetic energy K and reaches a maximum
height h.
a) 2h
B
b) 4h
c) 8h
d) 16h
Tips: Conservation of Mech E EB=ET
KB=UGT
Find relationship between K and h
KB=mgh
h=KB/mg (if 4x K, h increases 4xs)
28. What's the max speed (w/o slipping) a car can
have on a flat circular track with μs & radius R?
B
Tip: Car is moving in a
circular path, so there
must be a centripetal
force. Draw FBD. Apply
Newtons 2nd.
FN
Note – Only b has the
correct units
fS
FC =  Fr = mv 2 / R
mg
fs max = mvmax / R
2
m s mg = mvmax 2 / R
vmax = m s gR
a) msgR
b) (msgR)
c) (ms/gR)
d) ms/gR
29. A 2 kg ball is thrown downward with an initial
speed of 20 m/s from the top of a 50 m cliff.
a) 900 J
b) 1400 J
c) 400 J
ET  W f = EB
D
W f = EB  ET
W f = ( K B  U gB )  ( K T  U gT )
= 12 mvB  ( 12 mvT  mghT )
2
d) 500 J
2
= 30 2  (20 2  1000) = 900  1400 = 500 J
30. A 5 kg bowling ball
is tied to a string and
hung from the
ceiling of an
elevator, as shown.
D
FT
a=-3m/s2
mg
Tip: Forces and accel –
draw FBD, apply
Newtons 2nd
F
y
= ma y
FT  mg = ma y
FT = mg  ma y = 5(10  3) = 35 N
a) 50 N
b) 65 N
c) -15 N
d) 35 N
31. A ball is dropped. Which graph shows its kinetic
energy vs. time as it falls?
C
Tips: K is directly related to v2
How is v2 related to t? v=gt and v2=g2t2
Therefore K is related to t2. It is a parabolic relationship
32. A 5 kg bowling ball
is tied to a string and
hung from the ceiling
of an elevator, as
shown.
A
FT
mg
Tips: Forces and accel – draw
FBD, apply Newtons 2nd .
CONSTANT SPEED means NO
ACCEL. Circle it everytime you
see it. All forces on ball are
balanced
a) 50 N
b) 25 N
c) 75 N
d) 0 N
33. A box of mass m is attached to a spring with a
spring constant k.
Set Ug = 0 at level of box.
Initial – spring is
stretched, all energy is US
Final – spring at equilib
and block at rest.
D
a) kd2/(mg)
c) kd/(mg)
b) kd2/(2mg)
d) kd/(2mg)
Ei + Wf = Ef
1/2kd2 + fkd = 0
1/2kd2 + mkmgd = 0
mk = kd/(2mg)
Tip: Cant use kinematics with springs because the spring
force (and acceleration) is not constant. Use conservation of
energy (Ei+WNC=EF). Work done by friction removes mech E
34. A box hangs stationary on the end of a vertical
spring with a spring constant k.
Fspr = mg
kx = mg
m = kx/g
Fspr
A
mg
a) kx/g
Tip: draw FBD, block is at rest, all forces are
balanced Since block is at rest
Can eliminate c because the units are not kg
b) kx/(2g)
c) kx2/(2g)
d) 2kx/g
35. Which graph shows the correct potential
energy U of a standard spring vs. its stretch, x?
C US=1/2kx2