Download Introduction to Artificial Intelligence – Course 67842

The Hebrew University of Jerusalem
School of Engineering and Computer Science
Instructor: Jeff Rosenschein
(Chapters 5 and 6, “Artificial Intelligence: A Modern Approach”)




Constraint Satisfaction Problems (CSP)
Backtracking search for CSPs
Problem Structure and Problem
Decomposition
Local search for CSPs
2

Standard search problem:
◦ state is a “black box” – any data structure that
supports successor function, heuristic function, and
goal test



CSP:
◦ state is defined by variables Xi with values from
domain Di
◦ goal test is a set of constraints specifying allowable
combinations of values for subsets of variables
Simple example of a formal representation
language
Allows useful general-purpose algorithms with
more power than standard search algorithms

3





A CSP is a triplet {X, D, C}
X is a finite set of variables { X1, X2, … , XN}
Each variable Xi may be assigned a value from a domain
Di of values
Each member of C is a pair. The first member of each
pair is a set of variables. The second element is a set of
legal values which that set may take.
Example:
◦ X = { X1, X2, X3, X4, X5, X6}
◦ D = { R, G, B} In this case, all the variables’ domains are the same
◦ C = { (X1, X2) : { (R,G), (R,B), (G,R), (G,B), (B,R) (B,G)},
(X1, X3) : { (R,G), (R,B), (G,R), (G,B), (B,R) (B,G)}, … }

Obvious point: Usually C isn’t represented explicitly,
but by a function.
4




A state of the problem is defined by an
assignment of values to some or all of the
variables,
{Xi = vi, Xj = vj, …}
An assignment that does not violate any
constraints is called a consistent or legal
assignment
A complete assignment is one in which every
variable is mentioned, and a solution to a CSP is a
complete assignment that satisfies all the
constraints
Some CSPs also require a solution that maximizes
an objective function
5



Variables WA, NT, Q, NSW, V, SA, T
Domains Di = {red, green, blue}
Constraints: adjacent regions must have different colors
e.g., WA ≠ NT (if the language allows stating this so
succinctly), or
(WA, NT) in {(red,green), (red,blue), (green,red),
(green,blue), (blue,red), (blue,green)}

6

This is a solution: complete and consistent
assignments (i.e., all variables assigned, all
constraints satisfied):
e.g., WA = red, NT = green, Q = red, NSW =
green, V = red, SA = blue, T = green

7


Binary CSP: each constraint relates two variables
Constraint graph: nodes are variables, arcs show
constraints

General-purpose CSP algorithms use the graph structure to speed up
search, e.g., Tasmania is an independent subproblem
8

Discrete variables
◦ finite domains:
 n variables, domain size d implies O(dn) complete assignments
 e.g., Boolean CSPs, including Boolean satisfiability (NP-complete)
◦ infinite domains:





integers, strings, etc.
e.g., job scheduling, variables are start/end days for each job
need a constraint language, e.g., StartJob1 + 5 ≤ StartJob3
linear constraints solvable, nonlinear undecidable
Continuous variables
◦ e.g., start/end times for Hubble Space Telescope
observations
◦ linear constraints solvable in polynomial time by linear
programming methods
9

Unary constraints involve a single variable
◦ e.g., SA ≠ green

Binary constraints involve pairs of variables
◦ e.g., SA ≠ WA

Higher-order constraints involve 3 or more
variables
◦ e.g., cryptarithmetic column constraints

Preferences (soft constraints), e.g., red is
better than green, often representable by a
cost for each variable assignment
◦ constrained optimization problems
10



Variables: F T U W R O X1 X2 X3
Domains: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Constraints: Alldiff (F, T, U, W, R, O)
◦
◦
◦
◦
◦
O + O = R + 10 · X1
X1 + W + W = U + 10 · X2
X2 + T + T = O + 10 · X3
X3 = F, T ≠ 0, F ≠ 0
11

Assignment problems

Timetabling problems
◦ e.g., who teaches what class?
◦ e.g., which class (or exam) is offered when and
where?
◦ Ziv Wities’ HUJI Exam Scheduler (on Moodle)






Hardware Configuration
Spreadsheets
Transportation scheduling
Factory scheduling
Floorplanning
Notice that many real-world problems involve
real-valued variables

12






How about using a search algorithm?
Define: a search state has variables 1…k
assigned. Values k+1…n, as yet unassigned
Start state: All unassigned
Goal state: All assigned, and all constraints
satisfied
Successors of a state with V1…Vk assigned and
rest unassigned are all states (with V1…Vk the
same) with Vk+1 assigned a value from D
Cost on transitions: 0 or any
constant. We don’t care. We
just want any solution.
13
Let’s start with the straightforward (dumb) approach,
then fix it.
States are defined by the values assigned so far.
 Initial state: the empty assignment { }
 Successor function: assign a value to an unassigned
variable that does not conflict with current assignment
 fail if no legal assignments

1.
2.
3.
4.
5.
Goal test: the current assignment is complete
This is the same for all CSPs
(good)
Every solution appears at depth n with n variables
 use depth-first search
Path is irrelevant, so can also use complete-state
formulation
b = (n - l )d at depth l, hence n! · dn leaves
(bad)
b is branching factor, d is size of domain, n is number of variables
14

Let’s say we had 4 variables, each of which
could take one of 4 integer values
????
At start, all unassigned
4???
1??? 2??? 3???
?1?? ?2?? ?3?? ?4??
11??
12??
13??
14??
1?1?
1?2?
1?3?
??1? ??2? ??3? ??4?
1?4?
1??1
1??2
???1 ???2 ???3 ???4
1??3
1??43
Etc.…terrible
branching factor
15
But variable assignments are commutative,
i.e.,
[ WA = red then NT = green ] same as [ NT =
green then WA = red ]
 So only need to consider assignments to a
single variable at each node

 b = d and there are dn leaves



Depth-first search for CSPs with singlevariable assignments is called backtracking
search
Backtracking search is the basic uninformed
algorithm for CSPs
Can solve n-queens for n ≈ 25

16
17
18
19
20
21

http://www.cs.cmu.edu/~awm/animations/constraint/9d.htm
l
Tries Blue, then Red, then Black
Does not do very well…
22
23




Don’t try successor that causes inconsistency
with its neighbors
Backtracking still doesn’t look too good
http://www.cs.cmu.edu/~awm/animations/c
onstraint/9b.html
http://www.cs.cmu.edu/~awm/animations/c
onstraint/27b.html
24
25
26
27
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
◦ In what order should its values be tried?
◦ Can we detect inevitable failure early?
◦ Can we take advantage of problem
structure?
◦
28
• Which variable should
be assigned next?
• In what order should its
values be tried?
29
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
- SelectUnassignedVariable
◦ In what order should its values be tried?
- OrderDomainVariables
◦ Can we detect inevitable failure early?
◦ Can we take advantage of problem
structure?
◦
30
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
◦ In what order should its values be tried?
◦ Can we detect inevitable failure early?
◦ Can we take advantage of problem
structure?
◦
31

Minimum remaining values (MRV):
choose the variable with the fewest legal values
All are
the same
here
Two
equivalent
ones here
Clear
choice
32


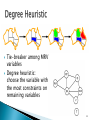
Tie-breaker among MRV
variables
Degree heuristic:
choose the variable with
the most constraints on
remaining variables
33
 General-purpose
methods can
give huge gains in speed:
◦ Which variable should be assigned
next? – we’ve seen 2 possibilities:
 Minimum Remaining Values (MRV)
 Degree Heuristic
◦
◦
34
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
◦ In what order should its values be tried?
◦ Can we detect inevitable failure early?
◦ Can we take advantage of problem
structure?
◦
35

Given a variable, choose the least constraining
value:
◦ the one that rules out the fewest values in the remaining
variables
◦

Combining the above three heuristics makes 1000
queens feasible

36
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
◦ In what order should its values be tried?
 Least Constraining Value

37
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
◦ In what order should its values be tried?
◦ Can we detect inevitable failure early?
◦ Can we take advantage of problem
structure?
◦
38

Idea:
◦ Keep track of remaining legal values for
unassigned variables
◦ Terminate search when any variable has no legal
values
◦
39

Idea:
◦ Keep track of remaining legal values for
unassigned variables
◦ Terminate search when any variable has no legal
values
◦
40

Idea:
◦ Keep track of remaining legal values for
unassigned variables
◦ Terminate search when any variable has no legal
values
◦
41

Idea:
◦ Keep track of remaining legal values for
unassigned variables
◦ Terminate search when any variable has no legal
values
◦
42
43
44

Forward checking propagates information
from assigned to unassigned variables, but
doesn’t provide early detection for all failures:



NT and SA cannot both be blue!
Constraint propagation repeatedly enforces
constraints locally

45


Forward checking computes the domain of
each variable independently at the start,
and then only updates these domains when
assignments are made in the DFS that are
directly relevant to the current variable.
Constraint Propagation carries this further.
When you delete a value from your domain,
check all variables connected to you. If any
of them change, delete all inconsistent
values connected to them, etc…
46
47
48


Simplest form of propagation makes each arc consistent
X Y is consistent iff
for every value x of X there is some allowed y
49


Simplest form of propagation makes each arc consistent
X Y is consistent iff
for every value x of X there is some allowed y
50


Simplest form of propagation makes each arc consistent
X Y is consistent iff
for every value x of X there is some allowed y

If X loses a value, neighbors of X need to be rechecked

51


Simplest form of propagation makes each arc consistent
X Y is consistent iff
for every value x of X there is some allowed y


If X loses a value, neighbors of X need to be rechecked
Arc consistency detects failure earlier than forward
checking

52
53
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
◦ In what order should its values be tried?
◦ Can we detect inevitable failure early?
 Forward Checking
 Constraint Propagation
 Arc Consistency

54
 General-purpose
methods can give
huge gains in speed:
◦ Which variable should be assigned next?
◦ In what order should its values be tried?
◦ Can we detect inevitable failure early?
◦ Can we take advantage of problem
structure?
◦
55


Tasmania and mainland are independent
subproblems
Subproblems identifiable as connected
components of constraint graph
56



Suppose each subproblem has c variables out of
n total (d is the size of the domain)
Worst-case solution cost is n/c * dc, linear in n
E.g., n=80, d=2, c=20
At 10 million nodes/sec, 280 = 4 billion years
At 10 million nodes/sec, 4 * 220 = 0.4 seconds
57



Theorem: if the constraint graph has no loops, the CSP
can be solved in O(nd2) time
Compare to general CSPs, where worst-case time is
O(dn)
This property also applies to logical and probabilistic
reasoning: an important example of the relationship
between syntactic restrictions and the complexity of
reasoning
58
1.
2.
3.
Choose a variable as root, order variables from root to leaves such
that every node’s parent precedes it in the ordering
For j from n down to 2, check for arc consistency, i.e., apply
RemoveInconsistentValues(Parent(Xj), Xj), removing values from the
domain of the parent node, as necessary
For j from 1 to n, assign Xj consistently with Parent(Xj)
In Step 2, going from n down to 2 ensures that deleted values don’t endanger the
consistency of already-processed arcs;
Step 3 requires no backtracking (the CSP is by then directionally arc consistent).
59



Conditioning: instantiate a variable, prune its
neighbors’ domains – now we have a tree
Cutset conditioning: instantiate (in all ways – so
we don’t miss a solution) a set of variables
such that the remaining constraint graph is a
tree
Cutset size c implies runtime O(dc * (n – c)d2),
very fast for small c
60




Hill-climbing, simulated annealing typically
work with “complete” states, i.e., all
variables assigned
To apply to CSPs:
◦ use complete states, but with unsatisfied
constraints
◦ operators reassign variable values
Variable selection: randomly select any
conflicted variable
Value selection by min-conflicts heuristic:
◦ choose value that violates the fewest constraints
◦ i.e., hill-climb with h(n) = total number of
violated constraints
◦
61




States: 4 queens in 4 columns (44 = 256 states)
Actions: move queen in column
Goal test: no attacks
Evaluation: h(n) = number of attacks



62


Given random initial state, can solve n-queens
in almost constant time for arbitrary n with
high probability (e.g., n = 10,000,000)
The same appears to be true for any randomly
generated CSP except in a narrow range of the
ratio:
63

(The following slides used by permission of Andrew Moore,
computer science professor at Carnegie Mellon University, now
setting up Google’s Pittsburgh office)
◦ http://www.cs.cmu.edu/~awm/tutorials

Selecting a move in the game of
“minesweeper”
0
0
1
0
0
1
0
0
1
1
1
2
Which squares have a bomb? Squares with numbers don’t. Other squares
might. Numbers tell how many of the eight adjacent squares have bombs.
We want to find out if a given square can possibly have a bomb….
Slide 64
0
0
1
V1
0
0
1
V2
0
0
1
V3
1
1
2
V4
V8 V7 V6 V5
V = { V1 , V2 , V3 , V4 , V5 , V6 , V7 , V8 }, D = { B (bomb) , S (space) }
C = { (V1, V2) : { (B,S) , (S,B) }, (V1, V2, V3,) : { (B,S,S) , (S,B,S) , (S,S,B)},…}
V1
V2
V8
V3
V7
V6
V4
V5
Slide 65
One of the earliest examples of a computation posed as a CSP.
The Waltz algorithm is for interpreting line drawings of solid
polyhedra.
Look at all intersections.
What kind of intersection could this be? A
concave intersection of three faces? Or
an external convex intersection?
Adjacent intersections impose constraints on each other.
Use CSP to find a unique set of labelings. Important step to
“understanding” the image.
66
Assume all objects:
• Have no shadows or cracks
• Three-faced vertices
• “General position”: no junctions change with small
movements of the eye.
Then each line on image is one of the following:
• Boundary line (edge of an object) (<) with right hand of
arrow denoting “solid” and left hand denoting “space”
• Interior convex edge (+)
• Interior concave edge (-)
67
Given a representation of the diagram, label each junction in one of the
above manners.
The junctions must be labeled so that lines are labeled consistently at
both ends.
Can you formulate that as a CSP? FUN FACT: Constraint Propagation
always works perfectly.
68
69
70







CSPs are a special kind of search problem:
◦ states defined by values of a fixed set of variables
◦ goal test defined by constraints on variable values
Backtracking = depth-first search with one variable
assigned per node
Variable ordering (MRV, degree heuristic) and value
selection (least constraining value) heuristics help
significantly
Forward checking prevents assignments that
guarantee later failure
Constraint propagation (e.g., arc consistency) does
additional work to constrain values and detect
inconsistencies
The CSP representation allows analysis of problem
structure
Tree-structured CSPs can be solved in linear time
 Iterative min-conflicts is usually effective in practice

71
Chapter 5
Sections 1 – 4, 6


Games
Perfect Play
◦ minimax decisions
◦ α-β pruning



Resource limits and approximate evaluation
Games of chance
Games of imperfect information
73



“Unpredictable” opponent  solution is a strategy,
specifying a move for every possible opponent reply
Time limits  unlikely to find goal, must approximate
Plan of attack:
◦ Computer considers all lines of play (Babbage, 1846)
◦ Algorithm for perfect play (Zermolo, 1912; Von Neumann, 1944)
◦ Finite horizon, approximate evaluation (Zuse, 1945; Wiener, 1948;
Shannon, 1950)
◦ First chess program (Turing, 1951)
◦ Machine learning to improve evaluation accuracy (Samuel, 19521957)
◦ Pruning to allow deeper search (McCarthy, 1956)
◦
74
75
76



Perfect play for deterministic games
Idea: choose move to position with highest
minimax value
= best achievable payoff against best play
E.g., 2-ply game:

77
78




Complete? Only if tree is finite (chess has
specific rules for this); note that a finite
strategy can exist even in an infinite tree
Optimal? Yes, against an optimal opponent;
otherwise?
Time complexity? O(bm) (b = legal moves, m =
maximum depth of tree)
Space complexity? O(bm) (depth-first
exploration
◦ For chess, b ≈ 35, m ≈100 for “reasonable” games
 exact solution completely infeasible
◦
But do we need to explore every path?
79
80
81
82
83
84


α is the value of the
best (i.e., highestvalue) choice found
so far at any choice
point along the path
for max
If v is worse than α,
max will avoid it
 prune that branch

Define β similarly for
min

85
86
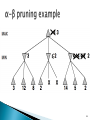
Extended
example
of α-β
87



Pruning does not affect final result
Good move ordering improves effectiveness of
pruning
With “perfect ordering” time complexity=O(bm/2)
 doubles depth of search



(In worst case, there is no improvement)
A simple example of the value of reasoning about
which computations are relevant (a form of
metareasoning)
Unfortunately, 3550 is still impossible…

88
Standard approach:
 Use Cutoff test instead of Terminal test:
e.g., depth limit (perhaps add quiescence search)

Use Eval instead of Utility
◦ i.e., evaluation function that estimates desirability of
position
Suppose we have 100 seconds, explore 104 nodes/sec
 106 nodes per move, approximately 358/2

4-ply lookahead is a hopeless chess player!
◦ 4-ply ≈ human novice
◦ 8-ply ≈ mid-level PC, human master
◦ 12-ply ≈ Deep Blue, Kasparov
α-β reaches depth 8, i.e., pretty good chess program
89


For chess, typically linear weighted sum of features
Eval(s) = w1 f1(s) + w2 f2(s) + … + wn fn(s)
e.g., w1 = 9 with
f1(s) = (number of white queens) – (number of black
queens), etc.
90


Behavior is preserved under any monotonic
transformation of Eval
Only the order matters:
◦ Payoff in deterministic games acts as an ordinal
utility function
91



Problem: Sometimes there are time limits on a move
Solution: Progressive Deepening (like Iterative Deepening
Search)
A “best move” is always ready; an “anytime algorithm”
92


Problem: Alpha-beta still doesn’t limit tree
growth enough
Solution: Heuristic pruning
◦ Order moves plausibly and concentrate on better
moves
◦ Does not guarantee the quality of our search
93



Problem: The Horizon Effect: Pushing an
inevitable loss beyond the field of view
Solution: Heuristic continuation
Continue search when an otherwise terminal
situation is judged to be particularly dynamic
— waiting for quiescence
94



Secondary search – check more deeply into a
chosen move
Book moves – use a “table lookup” –
sometimes is feasible (beginning or end of
game)
Limitations of all these methods:
◦ Need to get a single number to reflect a position
◦ Assumption of opponent’s infallibility
95


Checkers: Chinook ended 40-year-reign of
human world champion Marion Tinsley in 1994.
Used a precomputed endgame database defining
perfect play for all positions involving 8 or fewer
pieces on the board, a total of 443,748,401,247
positions.
A precomputed endgame database? Would it be
possible to extend the “endgame” all the way
back to the beginning of the game, essentially
“solving” checkers?
96
Originally published in Science Express on 19 July 2007
Science 14 September 2007:
Vol. 317, no. 5844, pp. 1518 – 1522
Jonathan Schaeffer (University of Alberta), Neil Burch, Yngvi Björnsson,
Akihiro Kishimoto, Martin Müller, Robert Lake, Paul Lu, Steve Sutphen
The game of checkers has roughly 500 billion billion possible positions
(5 x 1020). The task of solving the game, determining the final result
in a game with no mistakes made by either player, is daunting. Since
1989, almost continuously, dozens of computers have been working
on solving checkers, applying state-of-the-art artificial intelligence
techniques to the proving process. This paper announces that
checkers is now solved: Perfect play by both sides leads to a draw.
This is the most challenging popular game to be solved to date,
roughly one million times as complex as Connect Four. Artificial
intelligence technology has been used to generate strong heuristicbased game-playing programs, such as Deep Blue for chess. Solving
a game takes this to the next level by replacing the heuristics with
perfection.
97



Chess: Deep Blue defeated human world champion
Garry Kasparov in a six-game match in 1997. Deep
Blue searches 200 million positions per second, uses
very sophisticated evaluation, and undisclosed methods
for extending some lines of search up to 40 ply. Rybka
was the 2008 and 2009 computer chess champion
(uses an off-the-shelf 8-core 3.2GHz Intel Xeon
processor), but was stripped of its titles for having
plagiarized two other programs…
Othello: Logistello beats human world champion in
1997; human champions refuse to compete against
computers, who are too good
Go: human champions refuse to compete against
computers, who are too bad. In go, b > 300, so most
programs use pattern knowledge bases to suggest
plausible moves.
98


Games are fun to work on!
They illustrate several important points about AI
◦
◦
◦
◦

Perfection is unattainable  must approximate
Good idea to think about what to think about
Uncertainty constrains the assignment of values to states
Optimal decisions depend on information state, not real
state
Games are to AI as grand prix racing is to
automobile design
99