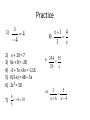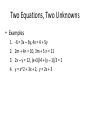Download Math review (1 OF 2) 2 equations w 2 unknowns

Honors Physics
Math Review
Key Math Skills Needed for Success!
• Conversions
– Know metric conversion factors
– Know how to properly convert from one unit to
another
• Scientific Notation
– How to convert between scientific notation and
standard notation
• Algebra
– Solve for x
• Geometry/Trig
– SOHCAHTOA
Conversions
• Metric Base units (100)
– Definition: Fundamental unit
– Mass: gram (g)
– Length: meter (m)
– Time: seconds (s)
– Temperature: kelvin (K)
– Amount of substance: mole (mol)
– Volume: Liter (L)
Conversions
• Prefixes
– Greater than base unit
•
•
•
•
Deca- (101), Hecto- (102), Kilo- (103)
Deca- = ten, Hecto- = hundred, Kilo- = thousand
Abbreviations: Deca  da, Hecto  h, Kilo  k
Example: 1 hectometer is the same as saying 100 meters or
102 meters
– Less than base unit
•
•
•
•
Deci- (10-1), Centi- (10-2), Milli- (10-3)
Deci- = 1/10, Centi- = 1/100, Milli- = 1/1000
Abbreviations: Deci  d, Centi  c, Milli  m
Example: 1 centimeter is the same as saying one onehundreth of a meter or 10-2 meters
Conversions
• Conversion factors
– All conversion factors must equal 1
– Conversion factors take the form of a fraction
– Just as 5/5, 28/28, and 142/142 all equal 1, there
are multiple ways of writing conversion factors
that equal 1.
– Example: __100 cm__, __1 km__, __1000m__
1m
1000m
1 km
Conversions
• Conversion Factors
– How to read them
• Example: __1000 mm__, there are 1000
1m
millimeters in 1 meter.
• Ask yourself, “Does this make sense?”
– How to properly write them
• The smaller unit always gets the number greater than 1
Practice
• Write the conversion factors you would use to
convert from…
– cm to m
– m to cm
– kg to g
– g to kg
– ms to s
– s to ms
Conversions
• How do I know which unit goes in the
numerator and which unit goes in the
denominator when making my conversion
factor?
– The unit that you are converting FROM always
goes in the denominator
– The unit you are converting TO always goes in the
numerator
Practice
• Convert the following (make sure to properly
write your conversion factor):
– 42 cg = ? g
– 6 m = ? km
– 132 ms = ? s
– 86 kg = ? g
Conversions
• What if I am not converting to my base unit?
For example, 58 cm = ? km
– First convert your know quantity to your base unit
• 58 centimeters equals how many meters
• 58 cm = .58 m
– Second convert your base unit to your desired unit
• .58 meters equals how many kilometers
• .58 m = .00058 km
Practice
•
•
•
•
•
9 mm = ? cm
18 kg = ? dag
95 mg = ? kg
63 cg = ? hg
1,468 dm = ? km
Scientific Notation
• Scientific notation makes the expression of
very large or very small numbers simpler.
• Makes it easier to keep track of significant
figures.
• In Physics, you will deal with very large
numbers such as the distance from the sun to
the Earth which is 149,600,000,000 meters.
Scientific Notation
• General form: a x 10n
– a must be a number between 1 and 10
– n must be an integer
– Example: These are NOT in scientific notation
• 34 x 105… Why?
• 4.8 x 100.5… Why?
Scientific Notation
• What’s the difference between a positive
exponent and a negative exponent?
– Positive exponents tell you how many times to
multiply by 10
– Negative exponents tell you how many times to
divide by 10
Scientific Notation
• Converting from standard form to scientific
notation
– Remember… a x 10n
– Move the decimal point left or right until you wind
up with a number between 1 and 10
• The number you are left with is “a”
– The number of spaces the decimal point is moved
is the exponent “n”
Scientific Notation
• Converting from standard notation to scientific
notation…how do I know if my exponent is
positive or negative?
– If the decimal is moved to the left, you will have a
positive exponent
• In other words, “a” is less than the number you started with
– If the decimal is moved to the right, you will have a
negative exponent
• In other words, “a” is greater than what you started with
Practice
• Write 3,040 in scientific notation
• Write 0.00012 in scientific notation
• Write 149,600,000,000 in scientific notation
– The distance from Earth to the sun
• How many kilometers are in 1 meter? (write
the answer in scientific notation)
• How many milligrams are in 1 kilogram? (write
the answer in scientific notation)
Scientific Notation
• Converting from scientific notation to standard
form
– Remember… a x 10n
– If “n” is positive, move the decimal point in “a” to the
right
• In other words, if “n” is positive your answer will be greater
than your original “a”
– If “n” is negative, move the decimal point in “a” to the
left
• In other words, if “n” is negative your answer will be less
than your original “a”
Scientific Notation
• How to enter a number in scientific notation
into your calculator.
– Remember… a x 10n
– Enter “a”
– Press the “EE” button
– Enter “n”
– Do NOT press the multiplication button or enter
the number 10
• “EE” takes the place of this step
Practice
• Write the following in standard form
– 4.01 x 102
– 5.7 x 10-3
– 8.9 x 105
– 6 x 10-1
Algebra
• Solving for “x”
• Key things to remember
– What you do to the left side of the equation you
MUST do to the right side of the equation.
– What you do to one term you must do to ALL terms
on both sides of the equation
• Think back to… order of operations
– Please excuse my dear aunt sally
– Parentheses exponents multiply divide add subtract
– Left to right
Algebra
• Solving for “x”
• First combine all like terms abiding by order of
operations
– Remember…
• variables do NOT mix with non-variables
• 1x + 1x = 2x, 3x + 4x = 7x
• x(x) = x², 2x(6x) = 12x², 2x(3x²) = 6x³
– Example: 3x + 14 – 5x + x = 2 + 1 + 3(5) – 6x
14 – x = 18 – 6x
Algebra
• Solving for “x”
• Second, move all terms containing a variable to
one side of the equation and all other terms to
the other side.
• Remember…
– Opposite of addition is subtraction and vice versa
– Opposite of multiplication is division and vice versa
• Example: 14 – x = 18 – 6x
5x = 4
Algebra
• Solving for “x”
• Finally, make it so that the coefficient of “x” is
1
– This means divide both sides by the coefficient of
“x”
– If there are multiple terms on the opposite side,
make sure to divide each term by the coefficient
– Example: 5x = 4
x = 4/5
Algebra
• If the variable is in the denominator use cross
multiplication
• For example…
1. 54 72

d 64
2.
y  15 35

y4
7
Algebra
• Solving for “x”
– If your “x” term is squared then make your last
step to take the square root of both sides of the
equation
– Remember…
• you can plug your answer back into the equation
– If the left side of the equation equals the right side then you
solved for “x” correctly!
Practice
1)
2)
3)
4)
5)
6)
x
4
4
x + 10 = 7
6x + 8 = -28
-6 + 7x +3x = -116
6(3-x) = 48 – 3x
2x² = 50
6
x  4  10
7)
5
x 1 4
8)

3
x
9)
10)
354 55

20
x
3
5

w6 w4
Two Equations, Two Unknowns
• System of Equations: set of 2 or more
equations that use the same variables.
2x – y = 7, 4x + 3y = 4
• Solve by substitution:
1. Solve for one of the variables.
 2x – y = 7  y = 2x - 7
Two Equations, Two Unknowns
2. Substitute the expression for the variable that you
solved step 1 for into the second equation.
 4x + 3y = 4  4x + 3(2x – 7) = 4  x = 2.5
3. Substitute the value of x into either equation.
 y = 2x – 7  y = 2(2.5) – 7  y = -2
Quadratic Equation
• When solving an equation in the form, ax^2 +
bx + c = 0, you may need to use the quadratic
formula if reverse FOIL does not work
Two Equations, Two Unknowns
• Examples
1.
2.
3.
4.
-6 = 3x – 6y, 4x = 4 + 5y
2m + 4n = 10, 3m + 5 n = 11
2x – y = 12, (x+3)/4 + (y – 1)/3 = 1
y = x^2 + 3x + 2, y = 2x + 3