Download cs621-lect19-fuzzy-logic-neural-net-based-IR-2008-10

CS621 : Artificial Intelligence
Pushpak Bhattacharyya
CSE Dept.,
IIT Bombay
Lecture 19: Fuzzy Logic and Neural Net Based IR
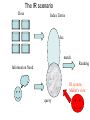
The IR scenario
Docs
Index Terms
doc
match
Ranking
Information Need
IR system
Maker’s view
query
Definition of IR Model
An IR model is a quadrupul
[D, Q, F, R(qi, dj)]
Where,
D: documents
Q: Queries
F: Framework for modeling document, query and their
relationships
R(.,.): Ranking function returning a real no. expressing
the relevance of dj with qi
The Boolean Model
• Simple model based on set theory
• Only AND, OR and NOT are used
• Queries specified as boolean expressions
– precise semantics
– neat formalism
– q = ka  (kb  kc)
• Terms are either present or absent. Thus, wij  {0,1}
• Consider
– q = ka  (kb  kc)
– vec(qdnf) = (1,1,1)  (1,1,0)  (1,0,0)
– vec(qcc) = (1,1,0) is a conjunctive component
The Boolean Model
Ka
• q = ka  (kb  kc)
Kb
(1,0,0)
(1,1,0)
(1,1,1)
• sim(q,dj) = 1 if
 vec(qcc) |
(vec(qcc)  vec(qdnf)) 
(ki, gi(vec(dj)) = gi(vec(qcc)))
Kc
0 otherwise
Fuzzy Set Model
• Queries and docs represented by sets of index
terms: matching is approximate from the start
• This vagueness can be modeled using a fuzzy
framework, as follows:
– with each term is associated a fuzzy set
– each doc has a degree of membership in this
fuzzy set
• This interpretation provides the foundation for
many models for IR based on fuzzy theory
• In here, we discuss the model proposed by
Ogawa, Morita, and Kobayashi (1991)
Fuzzy Set Theory
• Definition
– A fuzzy subset A of U is characterized by a
membership function
(A,u) : U  [0,1]
which associates with each element u of U a
number (u) in the interval [0,1]
• Definition
– Let A and B be two fuzzy subsets of U. Also, let ¬A
be the complement of A. Then,
• (¬A,u) = 1 - (A,u)
• (AB,u) = max((A,u), (B,u))
• (AB,u) = min((A,u), (B,u))
Fuzzy Information Retrieval
• Fuzzy sets are modeled based on a thesaurus
• This thesaurus is built as follows:
– Let vec(c) be a term-term correlation matrix
– Let c(i,l) be a normalized correlation factor for (ki,kl):
c(i,l) =
n(i,l)
ni + nl - n(i,l)
– ni: number of docs which contain ki
– nl: number of docs which contain kl
– n(i,l): number of docs which contain both ki and kl
• We now have the notion of proximity among index terms.
Fuzzy Information Retrieval
• The correlation factor c(i,l) can be used to define
fuzzy set membership for a document dj as follows:
(i,j) = 1 - 
(1 - c(i,l))
ki  dj
–(i,j) : membership of doc dj in fuzzy subset
associated with ki
• The above expression computes an algebraic sum
over all terms in the doc dj
• A doc dj belongs to the fuzzy set for ki, if its own
terms are associated with ki
Fuzzy Information Retrieval
•
(i,j) = 1 - 
(1 - c(i,l))
ki  dj
–(i,j) : membership of doc dj in fuzzy subset
associated with ki
• If doc dj contains a term kl which is closely related to
ki, we have
– c(i,l) ~ 1
– (i,j) ~ 1
– index ki is a good fuzzy index for doc
Fuzzy IR: An Example
Ka
cc3
Kb
cc2
cc1
• q = ka  (kb  kc)
• vec(qdnf) = (1,1,1) + (1,1,0) + (1,0,0)
= vec(cc1) + vec(cc2) + vec(cc3)
• (q,dj) = (cc1+cc2+cc3,j)
= 1 - (1 - (a,j) (b,j) (c,j)) *
(1 - (a,j) (b,j) (1-(c,j))) *
(1 - (a,j) (1-(b,j)) (1-(c,j)))
Kc
Fuzzy Information Retrieval
• Fuzzy IR models have been discussed mainly in the
literature associated with fuzzy theory
• Experiments with standard test collections are not
available
• Difficult to compare at this time
Basic of Neural Network
The human brain
Seat of consciousness and cognition
Perhaps the most complex information processing
machine in nature
Historically, considered as a monolithic information
processing machine
Beginner’s Brain Map
Forebrain (Cerebral Cortex):
Language, maths, sensation,
movement, cognition, emotion
Midbrain: Information Routing;
involuntary controls
Cerebellum: Motor
Control
Hindbrain: Control of
breathing, heartbeat, blood
circulation
Spinal cord: Reflexes,
information highways between
body & brain
Brain : a computational machine?
Information processing: brains vs computers
 brains better at perception / cognition
 slower at numerical calculations
 parallel and distributed Processing
 associative memory
Brain : a computational machine? (contd.)
• Evolutionarily, brain has developed algorithms most
suitable for survival
• Algorithms unknown: the search is on
• Brain astonishing in the amount of information it
processes
– Typical computers: 109 operations/sec
– Housefly brain: 1011 operations/sec
Brain facts & figures
• Basic building block of nervous system: nerve cell
(neuron)
• ~ 1012 neurons in brain
• ~ 1015 connections between them
• Connections made at “synapses”
• The speed: events on millisecond scale in neurons,
nanosecond scale in silicon chips
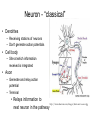
Neuron - “classical”
• Dendrites
– Receiving stations of neurons
– Don't generate action potentials
• Cell body
– Site at which information
received is integrated
• Axon
– Generate and relay action
potential
– Terminal
• Relays information to
http://www.educarer.com/images/brain-nerve-axon.jpg
next neuron in the pathway
Computation in Biological
Neuron
• Incoming signals from synapses are summed up at the
soma
•  , the biological “inner product”
• On crossing a threshold, the cell “fires” generating an
action potential in the axon hillock region
Synaptic inputs: Artist’s
conception
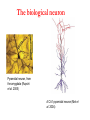
The biological neuron
Pyramidal neuron, from
the amygdala (Rupshi
et al. 2005)
A CA1 pyramidal neuron (Mel et
al. 2004)
A perspective of AI
Artificial Intelligence - Knowledge based computing
Disciplines which form the core of AI - inner circle
Fields which draw from these disciplines - outer circle.
Robotics
NLP
Expert
Systems
Search,
RSN,
LRN Planning
CV
Symbolic AI
Connectionist AI is contrasted with Symbolic AI
Symbolic AI - Physical Symbol System
Hypothesis
Every intelligent system can be
constructed by storing and processing
symbols and nothing more is necessary.
Symbolic AI has a bearing on models of
computation such as
Turing Machine
Von Neumann Machine
Lambda calculus
Turing Machine & Von Neumann Machine
Challenges to Symbolic AI
Motivation for challenging Symbolic AI
A large number of computations and
information process tasks that living beings are
comfortable with, are not performed well by
computers!
The Differences
Brain computation in living beings
Pattern Recognition
Learning oriented
Distributed & parallel processing
Content addressable
TM computation in computers
Numerical Processing
Programming oriented
Centralized & serial processing
Location addressable
Perceptron
The Perceptron Model
A perceptron is a computing element with input
lines having associated weights and the cell
having a threshold value. The perceptron model is
motivated by the biological neuron.
Output = y
Threshold = θ
wn
w1
Wn-1
Xn-1
x1
y
1
θ
Σwixi
Step function / Threshold function
y
= 1 for Σwixi >=θ
=0 otherwise
Features of Perceptron
• Input output behavior is discontinuous and the
derivative does not exist at Σwixi = θ
• Σwixi - θ is the net input denoted as net
• Referred to as a linear threshold element - linearity
because of x appearing with power 1
• y= f(net): Relation between y and net is non-linear
Computation of Boolean functions
AND of 2 inputs
X1
x2
y
0
0
0
0
1
0
1
0
0
1
1
1
The parameter values (weights & thresholds) need to be found.
y
θ
w1
w2
x1
x2
Computing parameter values
w1 * 0 + w2 * 0 <= θ  θ >= 0; since y=0
w1 * 0 + w2 * 1 <= θ  w2 <= θ; since y=0
w1 * 1 + w2 * 0 <= θ  w1 <= θ; since y=0
w1 * 1 + w2 *1 > θ  w1 + w2 > θ; since y=1
w1 = w2 = = 0.5
satisfy these inequalities and find parameters to be used for
computing AND function.
Other Boolean functions
• OR can be computed using values of w1 = w2 = 1
and = 0.5
• XOR function gives rise to the following
inequalities:
w1 * 0 + w2 * 0 <= θ  θ >= 0
w1 * 0 + w2 * 1 > θ  w2 > θ
w1 * 1 + w2 * 0 > θ  w1 > θ
w1 * 1 + w2 *1 <= θ  w1 + w2 <= θ
No set of parameter values satisfy these inequalities.
Threshold functions
n # Boolean functions (2^2^n) #Threshold Functions (2n^2)
1
4
4
2
16
14
3
256
128
4
64K
1008
•
•
•
Functions computable by perceptrons - threshold
functions
#TF becomes negligibly small for larger values of
#BF.
For n=2, all functions except XOR and XNOR are
computable.