Download CONTENTS - Resource Packet

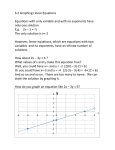
MATHEMATICS SUMMER REVIEW
RESOURCE PACKET
CONTENTS
REVIEW SECTION 1 – ORDER OF OPERATIONS
Vocabulary
Numerical Expression: An expression, such as 6 + 5, that consists of
numerals combined by operations and names a particular number, called the
value of the expression.
Algebraic Expression: An expression, such as 2x + 3, that consists of
numerals and variables combined with operations.
Each numerical expression should have a unique value. In order to avoid
misunderstandings and errors, mathematicians have agreed on certain rules
for computation called Order of Operations. (PEMDAS)
Order of Operations
P
Represents grouping or inclusion symbols. The basic grouping symbols
are parentheses ( ), brackets [ ], and the fraction bar. Expressions
within grouping symbols should be treated as a single value and should
be evaluated first. The fraction bar indicates that the numerator and
the denominator should each be treated as a single value. When more
than one grouping symbol is used, evaluate within the innermost
grouping symbol first.
E
Represents exponents. Perform all operations with exponents.
M
D
Multiplication and Division are considered to be on the same level
of operational importance. Therefore, perform all multiplication and
division in order from left to right.
1
A
S
Addition and Subtraction are also on the same level of operational
importance. Perform all addition and subtraction in order from left
to right.
To simplify or evaluate a numerical expression means to apply the Order
of Operations to replace a numerical expression by the simplest name of its
value.
Example 1:
Evaluate 3  12  4
3  12  4  3  3  0
first
Example 2: Evaluate 62  4  3  72
62  4  3  72  36  4  3  49
 36  12  49
 24  49  73
2
2
Example 3: Evaluate 3 2  5   7
2
3 2  5   7  3  7   7
 3  49   7
 147  7  21
To evaluate an algebraic expression means to replace each variable by a
given value and then apply the Order of Operations to simplify the result.
Example 4: Evaluate
a2  2
if a  5 and b  3
a  b3
a 2  2 52  2 25  2 23



a  b 3 5  33 5  27 32
Example 5: Evaluate
2
2
8  a  b   3b  if a  5 and b  2


3
2
2
2
2
2
2
8  a  b   3b   8 5  2   3  2  8 3  3  2






3
3
3
2
2
2
 8  9  3  2  72  6  78  52
3
3
3
2
REVIEW SECTION 2 – OPERATIONS WITH FRACTIONS
Multiplication Rule for Fractions: To multiply fractions, multiply numerators
and multiply denominators.
a c
ac
 
b d bd
Example 1:
3 5 15
 
4 8 32
Example 2:
5 9 45 3



6 10 60 4
Answers should always be given in
simplest form which means the
numerator and denominator have no
common factor other than 1. You can
multiply first and then simplify or
simplify first and then multiply.
or
1
3
2
2
5 9
3


6 10 4
Division Rule for Fractions: To divide fractions, multiply the numerator by
the reciprocal of the divisor.
a c a d ad
   
b d b c bc
Example 3:
3 2 3 7 21
   
5 7 5 2 10
Recall: The reciprocal of a number n is
Example 4:
2
2 1
1
 10  

9
9 10 45
3
1
.
n
Addition and Subtraction Rules for Fractions: To add or subtract fractions,
you must have common denominators. If fractions have different
denominators, rewrite the fractions using their least common denominator.
Then add or subtract the numerators and write the result over the common
denominator. Simplify if needed.
a b a b
 
c c
c
Example 5:
3 1 31 4
 

5 5
5
5
Example 6:
5 1 5 3 5 3 2
   

9 3 9 9
9
9
a b a b
 
c c
c
1
Recall: A mixed number is the sum of an integer and a fraction, such as 2 .
3
For our purposes in Algebra, all mixed numbers should be written as a single
fraction.
1
1 2 1 6 1 7
2     
3
3 1 3 3 3 3
Example 7:
2
Example 8:
3
3
3  3
15  3 
18
 3
 3            
    
5
1  5
5  5
5
 5
4
REVIEW SECTION 3 – THE REAL NUMBER SYSTEM
All of the math problems you have solved so far have used numbers from the
Real Number system. The set of numbers in the Real Number system is
often abbreviated by the symbol R. If you were to point to any location on a
number line, that location could be represented by a Real Number. As a
result, since there are an infinite number of locations on a number line, then
the set of R is infinitely large.
There are several categories of numbers, or subsets, within the set of R. If
you compare the definitions carefully, you will see that each subset is built
upon the previous subset of numbers, each with its own symbol. They
include:
Definition of Set
Name
Symbol
Natural
(Counting)
N
Whole
W
Integer
Z
Rational
Q
Natural numbers are sometimes called Counting numbers since
they represent the numbers you would use to count out
something such as the number of apples from a fruit stand in
a supermarket. The set of N is given in set notation as
1,2,3, 4,... . The three periods indicate that the set
continues infinitely with the given pattern.
The set of Whole numbers is the same as the set of N but
also includes 0. The set of W is given in set notation as
0,1,2,3, 4,... .
The set of Integers is given by the set of W and their
opposites. The set of Z is given in set notation as
...  3,  2,  2,0, 1, 2, 3,... . Notice that this set continues
infinitely in both the positive and negative directions.
The set of Rational numbers is defined as any number that
can be written as a fraction where both the numerator and
denominator are Integers. Some examples of Rational
numbers are:
1 9
, ,  22
2 5
Irrational
I
22 
0


 rewritten as  , 0  rewritten as  , etc.
1 
1


Notice that the N, W, and Z sets can therefore also be
classified as Rational numbers.
A number that is not a Rational number is considered to be
Irrational. Examples of Irrational Numbers are
2,  , 0.4257349369... (no pattern)
5
Sometimes it is convenient to represent the relationship between all of the
sets within the Real Number system by using either a Venn Diagram or a
“Family Tree” Diagram:
THE REAL NUMBERS SYSTEM, R
Venn Diagram
“Family Tree” Diagram
R
R
Q
Q
Z
I
I
Z
W
W
N
N
To name the sets of numbers to which a specific number belongs, use the
following process:
1) Since all numbers used so far are Real, always start by listing R.
(During Algebra II, you will learn about a different number system
that uses what are called Imaginary Numbers)
2) Continue by considering whether the number meets the
requirements for a Natural number. If it is a Natural number,
then it may also be automatically classified as W, Z and Q since
Natural numbers are subsets of each of these other sets.
3) If it is not a Natural number, decide if it meets the requirements
for a Whole number. If it is a Whole number, then it may
automatically be classified as Z and Q as well.
4) If it is not a Whole number, repeat the comparison for Integers.
5) If it is not an Integer but is written as a fraction, determine if
both the numerator and denominator are Integers. If they are
Integers, then the number is Rational. If either the numerator or
denominator is not an Integer but the fraction can be simplified to
Integers in both positions, then the number is Rational. If the
fraction cannot be simplified to the quotient of two integers, then
the number is Irrational.
6) If the number is not a fraction and does not meet any of the
requirements for N, W, Z, or Q, then it must be Irrational.
6
Name all of the number sets to which the following numbers belong:
Example 1:
17
R
N
W
Z
Q
All numbers considered so far are Real.
17 is a “counting” number so it is Natural.
All Natural numbers are Whole numbers.
All Natural numbers are Integers.
All Natural numbers are Rational.
(can be rewritten as  17  .
 1 
Example 2:
0
I
Not Irrational since it is Rational.
R
N
W
Z
Q
All numbers considered so far are Real.
Not Natural since 0 is NOT a “counting” number.
0 is first number in the Whole number set.
All Whole numbers are Integers.
All Whole numbers are Rational
(can be rewritten as  0  .
1
Example 3:
Example 4:
1
3
4
2
3
I
Not Irrational since it is Rational.
R
All numbers considered so far are Real.
N
W
Z
Not Natural since it is not a “counting” number.
Not a Whole number.
Not an Integer. On a number line, 1 3 is
Q
between the integers –2 and –1.
Rational because when rewritten as
I
the numerator and denominator are Integers.
Not Irrational since it is Rational.
4

7
4
, both
The approximate value of this number as determined
from
R
N
W
Z
Q
I
a calculator is 0.471404521…
All numbers considered so far are Real.
Not Natural since it is not a “counting” number.
Not a Whole number.
Not an Integer. On a number line, this value is
between the integers 0 and 1.
Not Rational because when though it is
written as a fraction, the numerator 2 is not an
Integer.
Irrational since it is not Rational.
7
A final word about Rational vs. Irrational Numbers…
RATIONAL: If a number is Rational, then its decimal equivalent value is
either a) terminating or b) non-terminating with a repeating pattern. For
example:
a)
2
5
is equal to 0.4 which is a terminating decimal (only zeros appear
after the 4).
b) 1 is equal to 0.333… or 0.3 . This decimal is non-terminating (goes on
3
infinitely), but has a repeating pattern.
IRRATIONAL: If a number is Irrational, then its decimal equivalent value is
non-terminating and does not have a repeating pattern. For example:
c)  is equal to 3.141592564… which is a non-terminating decimal and
does not have a repeating pattern.
d) 2 is equal to 1.414213562… and is therefore Irrational.
*** CAUTION! ***
SQUARE ROOTS: Sometimes we jump to the conclusion that anytime we
see a square root sign (radical symbol) that the number must be Irrational.
But if the number under the square root sign (radicand) is a perfect square,
then the number is, in fact, Rational as well as Natural, Whole and Integer.
Example 5:
24
Example 6:
121
Example 7:
25
2
Since 24 is not a perfect square, this number is
Irrational.
Since 121 is a perfect square of 11, this number is
Rational.
Since 25 is a perfect square of 5 and this fraction
simplifies to
Example 8:

15
7
5
2
, it is Rational.
Since 15 is not a perfect square, this entire
fraction is considered Irrational.
8
REVIEW SECTION 4 - PROPERTIES OF REAL NUMBERS
Properties of Addition:
Property
Description
Closure
If two or more numbers are added,
then the sum of those numbers will
be a member of the same number
set as the addends.
Associative
Addends can be regrouped without
affecting the value of the
expression.
Commutative
The order of addends can be
changed without affecting the value
of the expression.
Identity Element
The Identity Element of addition is
(Additive Identity)
0 (zero) – adding 0 to any number
yields the same number.
Inverse Element
The Inverse Element of addition is
(Additive Inverse)
an Opposite – adding a number and
its opposite will yield the identity
element 0.
Properties of Multiplication:
Property
Description
Closure
Associative
Commutative
Identity Element
(Multiplicative Identity)
Inverse Element
(Multiplicative Inverse)
(Reciprocal)
If two or more numbers are
multiplied, then the product of
those numbers will be a member of
the same number set as the factors.
Factors can be regrouped without
affecting the value of the
expression.
The order of factors can be
changed without affecting the value
of the expression.
The Identity Element of
Multiplication is 1 (one) – multiplying
any number by 1 yields the same
number.
The Inverse Element of
Multiplication is the Reciprocal –
Multiplying any number by its
reciprocal will yield the identity
element of 1.
9
Example
If a and b are Real
numbers, then the sum
of a and b is also a Real
number.
(a  b )  c  a  (b  c )
a b b a
a 0 a
a  a  0
Example
If a and b are Real
numbers, then the
product of a and b is
also a Real number.
(a x b) x c = a x (b x c)
axb=bxa
ax1=a
a
1
1
a
Distributive Property:
Property
Distributive
Example
Multiplication of a sum or
difference of two numbers by
another number.
Properties of Equality
Property
Reflexive
Symmetric
Transitive
Substitution
Addition
Multiplication
3(x + y) = 3x + 3y
Description
a a
a x (b + c) = ab + ac
a x (b – c) = ab - ac
Description / Example
If a = b, then b = a
If a=b and b=c, then a=c
If a= b and m = b, then a = m
If a= b and c is a real number, then a + c = b + c
If a= b and c is a real number, then ac = bc
REVIEW SECTION 5 – SOLVING LINEAR EQUATIONS
1) Eliminate fractions from the equations using LCD
2) Distribute scalers (multiply using Distributive Property)
3) Undo +/4) Undo 

5) Undo ( )
Example 1:
2 f  7   2f  14
2f  14  2f  14
14   14
Distribute
Subtract 2f
Since -14 = -14 is always true, the original
equation is an identity and the solution set
includes all Real numbers.
Example 2:
20  3x   3x  5
20  5
Add 3x
Since 20  5, there are no solutions that
make it true. Therefore, there is no
solution for this equation (often given by
the Greek symbol phi  ).
10
Example 3:
2  x  5   10    3x  2 
2x  10  10  3x  2
Distribute
Combine like terms
Subtract 3x
Divide by -1
2x  3x  2
x  2
x 2
Example 4:
1
1
16  6x    9  15x 
2
3
1
1
6  16  6x   6   9  15x  Clear the fractions using LCD of 6
2
3
Simplify
3 16  6x   2  9  15x 
48  18x  18  30x
18x  30  30x
48x   30
30
48
5
x 
8
x 
Distribute
Add -48
Add -30x
Divide by -48
Reduce to simplest terms.
Example 5:
1
2
 2n   3n
5
3
1

2

15   2n   15   3n 
5

3

3  30n  10  45n
Multiply each side by 15
7  15n
7
 n
15
Example 6:
3 2
5
1
 x  x
2 3
6
4
1
3 2 
5
12   x   12  x  
4
2 3 
6
18  8x  10x  3
15  18x
5
x
6
11
Multiply each side by 12
LCD: 12
.
REVIEW SECTION 6 – SOLVING INEQUALITIES
IN ONE VARIABLE
The graph of an inequality in one variable is the set of points on a
number line that represent all solutions of the inequality.
Equivalent Inequalities are inequalities that have the same solution.
For all real numbers, a,b and c:
Addition Prop. of Inequalities
If a › b , then a + c › b + c
If a ‹ b , then a + c ‹ b + c
Subtraction Prop. of Inequalities
Mult. Prop. of Inequalities
If a › b , then a - c › b – c
If a ‹ b , then a - c ‹ b – c
For c › 0
If
If
If
If
For c < 0
Division Prop. of Inequalities
For c › 0
a›b,
a‹b,
a›b,
a‹b,
then
then
then
then
ac ›
ac ‹
ac ‹
ac ›
If a › b , then
If a ‹ b , then
For c ‹ 0
If a › b , then
If a ‹ b , then
NOTE: When you multiply or divide by a negative number
number “doing the work” is negative), the direction of the
inequality sign changes.
a b
›
c
c
a b
‹
c
c
a b
‹
c
c
a b
›
c
c
(i.e. the
Graphing Inequalities
Example 1: Graph 3 › x
Solution. Rewrite as x ‹ 3
Use an open circle for the ‹ or › inequality symbols.
-2
-1
0
1
2
3
4
Example 2: Graph x ≥ 4
Use a closed circle for the ≤ or ≥ inequality symbols.
2
12
3
4
5
6
7
8
bc
bc
bc
bc
Solving Inequalities and Graphing Solution
Example 3: Solve and Graph
x-7 › -6
x›1
Graph
-2
-1
Add 7 to each side
0
1
2
3
4
Example 4: Solve and Graph
x+2 ≤ 7
x≤5
Graph
2
3
Subtract 2 from each side
4
5
6
7
8
Compound Inequalities
A compound inequality consists of two inequalities connected by an
“and” or an “or” statement.
Example 5: x is greater than -4 and less than or equal to -2.
-4 ‹ x ≤ -2
Example 6: x is greater than -3 and less than -1
-3 ‹ x ‹ -1
Note that the manner in which the “and” type of compound inequality
is written n Examples 5 and 6 implies that the value of x is between
the lower (left) and upper (right) values of the compound inequality.
Example 7: x is greater than zero or less than -3
x ‹ -3 or x › 0
Note that an “or” type of compound inequality must be written as two
separate inequalities joined by “or.” This type of inequality cannot be
written as a continuous “string” as shown for “and” type inequalities in
Examples 5 and 6.
13
Graphing an “or” Type Compound Inequality
The graph of an “or” type of inequality represents the union of the
two separate inequalities (i.e. the solution set includes points that
work in one inequality, the other inequality or both inequalities).
Example 8: Graph x ‹ -2 or x › 2
-3
-2
-1
0
2
1
3
Graphing an “and” Type Compound Inequality
The graph of an “and” type of inequality represents the intersection
of the two separate inequalities (i.e. the solution set includes points
that must work in both inequalities).
Example 9: Graph 2  x  3
This compound inequality is the same as x ≥ -2 and x ‹ 3
-3
-2
-1
0
2
1
3
More Examples – Solving Inequalities with Various Strategies
Example 10: Solve and Graph
x
5
3
x › 15
0
Example 11: Solve and Graph
5
Multiply both sides by 3
to “clear” fractions.
10
15
20
-4x ≤ 8
x ≥ -2
-3
14
-2
25
30
Divide by –4 to solve
for x. Since dividing by
a negative number,
direction of inequality
sign must be changed.
-1
0
1
2
3
Example 12: Solve and Graph
3n + 2 › 14
3n › 12
n›4
2
Example 13: Solve and Graph
4
5
4(x - 1) ≥ 8
4x – 4 ≥ 8
4x ≥ 12
x≥3
1
Example 14: Solve and Graph
3
Add -2
Divide by 3
2
3
-3
-2
7
8
Distribute
Add 4
Divide by 4
4
11 – 2x ≥ 3x + 16
-2x ≥ 3x + 5
-5x ≥ 5
x ≤ -1
-4
6
-1
5
6
7
Subtract 11
Subtract 3x
Divide by -5
0
1
2
Example 15: Solve and Graph an “or” Compound Inequality
5x + 1 ‹ -4 or 6x – 2 ≥ 10
Solve each
5x ‹ -5 or
6x ≥ 12
inequality
x ‹ -1 or
x≥2
separately.
fractions.
-3
-2
-1
0
1
2
3
Example 16: Solve and Graph an “and” Compound Inequality
-9 ≤ -4x – 5 ‹ 3
Implied “and” Inequality.
-4 ≤ -4x ‹ 8
Add 5 to each expression.
1 ≥ x
› -2
Divide each expression
by –4; change direction
of inequality signs.
-2 ‹ x ≤ 1
Rewrite solution.
-3
-2
-1
0
1
2
3
Note: Compound inequalities with implied “and” are always
expressed with the lower value to the left [low -> high].
15
REVIEW SECTION 7 – SLOPE OF LINEAR EQUATIONS
When graphing a linear equation, the resultant line has a certain amount of
“steepness” associated with it. In order to quantify the amount of
steepness, we define the “slope” of the line as the following ratio:
Slope = m =
Change in y direction Rise
.

Change in x direction Run
The terms “Rise” and “Run” come from the phrase “Rise over Run” which is
commonly used in carpentry to describe the dimension of the vertical portion
of a step (Rise) as compared to the dimension of the horizontal or tread
portion of the step (Run). When taken together, Rise over Run tells the
story of the slope, or steepness, of the steps. The slope of a linear equation
is the same at any point along the graph of the equation.
7A. DETERMINING SLOPE DIRECTLY FROM A GRAPH
1) Identify the coordinates of a point on the graph where the line
crosses at the intersection of grid lines on the graph paper.
2) Identify a second point, which also crosses at the intersection of
grid lines.
3) Starting at the first point, draw a step using only vertical and
horizontal moves that will take you to the second point. The
amount of movement in the vertical direction is the “change in y”
and the amount of movement in the horizontal direction is the
“change in x.” Use these values to calculate the slope as shown
above.
NOTE:




Movement
Movement
Movement
Movement
 is a move in the positive y direction
 is a move in the negative y direction
 is a move in the positive x direction
 is a move in the negative x direction
16
Example: From the graph shown, two
convenient points are selected which
cross at the intersection of grid lines
on the graph paper. Since slope is the
same at all points along the graph, the
size of the “step” created does not
matter.
x   2
y   3
Based on a movement of +3 in the y
direction and +2 in the x direction, the
slope of this equation would be 3 .
2
7B
. DETERMINING SLOPE FROM TWO POINTS
Since the slope represents the ratio of change in y direction to
change in x direction, then slope may be calculated from two ordered
pair solutions (x1, y1) and (x2, y2) for the equation by the following
formula:
Difference in y coordinates  y2  y1  y
Slope = m =


Difference in x coordinates  x2  x1  x
Note: The triangular symbol (  ) is the Greek letter Delta and is used
in Math and Science to represent change. In this case,  represents
the change in x or y coordinates.
Example:
If the points (4,2) and (-1, 5) are two solutions of a linear
equation, then the slope of that equation may be calculated as
follows:
The ordered pair (4,2) is arbitrarily labeled Point1 and (-1,5) is
labeled Point2. The x and y coordinates for each point are
labeled using subscripts to keep track of the numbers that will
be used in the slope calculation.
m
Point 1
Point 2
( 4, 2 )
x1 , y1
(  1, 5 )
x2 , y2
change in y
52
3


change in x  1  4
5
17
7C. DETERMINING SLOPE FROM THE SLOPE-INTERCEPT
FORM OF AN EQUATION
If an equation is written in the slope intercept form of y=mx+b, then
the slope may be obtained directly from m, the numerical coefficient
of x.
Example:
Given the equation y  3x  1 , the slope of this equation will be
3
3
.
or
1
1
(See the Section 8A, Graphing Linear Equations using a Point and Slope
for more information on equivalent forms for the value of slope)
7D. SPECIAL VALUES OF SLOPE
 The slope of a horizontal line is always zero (0). Given any horizontal
line, the y-coordinates for all points on the line are identical. As a
result, since y  0 for any given x , then the slope of a horizontal
line is always equal to zero and the equation of the line becomes simply
y = “the y-coordinate.”
mhorizontal 
y 0

0
x x
 The slope of a vertical line is considered to be “Undefined” and is
sometimes called “No Slope.” Given any vertical line, the x
coordinates for all points on the line are identical. As a result, since
x  0 for any given y , then the slope is considered “Undefined”
since dividing by zero ( x  0 ) in the slope calculation is prohibited.
The equation of a vertical line then becomes simply x = “the
x-coordinate.”
mvertical 
y y

 Undefined
x 0
18
REVIEW SECTION 8 – GRAPHING LINEAR EQUATIONS
The graph of a linear equation is a straight line. When you first started to
graph linear equations, you probably picked several values of x, calculated
the corresponding values of y using the given equation, plotted the points
and then connected the points with a line. You have also learned to graph
linear equations by three other methods: a) using a given point on the line
and slope, b) using slope and y-intercept and c) using x and y-intercepts. In
Algebra 2H, you will be expected to be able to use these three “shortcut”
methods to graph linear equations. You will also be expected to develop a
linear equation from only a graph of the equation.
8A. GRAPHING LINEAR EQUATIONS USING A POINT AND SLOPE
1) If given a point on a line and the slope of the line through that point, the
location of the given point represents a starting point for drawing the
graph. Plot the given point.
2) The slope, commonly represented by the variable m, indicates the
direction to “move away” from this given point in a stepwise manner.
Using the location of the given point as a starting point, find a second
point on the graph by moving away from the given point using the vertical
and horizontal components given by the slope. Find one point on either
side of the given point to confirm the trend indicated by slope.
3) Draw a straight line through given point and the points constructed
through use of the slope.
A few notes on interpreting “direction of movement” from slope (m)
2
 If m = an integer value like 2, rewrite it as
to represent a move of 2 in
1
the positive y direction ( ) and 1 in the positive x direction (). Remember
that this value of slope could also be represented by
2
which would be 2 in
1
the negative y direction () and 1 in the negative x direction ().
 If m is a negative value like 
2
, remember that you can associate the
3
 2 
 2
negative sign with either the numerator 
 or the denominator 
 to
 3 
 3
obtain the correct direction of movement from a given point.
19
EXAMPLE:
Graph the equation of a line that goes through the
point (2, -1) and has a slope of 
3
.
4
Step 1:
Graph the given point in Quadrant IV as shown on the
graph below.
Step 2:
Plot additional points based on the stepwise movement
given by the slope. Since m = 
3
, then move away from
4
the given point by moving 3 units in the negative y
direction and then 4 units in the positive x direction
(i.e. y   3, x  4 ). Another option is to move 3 units in
the positive y direction followed by 4 units in the
negative x direction (i.e. y  3, x   4 ).
Step 3:
Draw a straight line through the given point and the
constructed points.
y
x   4
y   3
x
Starting point
at (2, -1)
y   3
x   4
A reminder about “Special Cases” where Slope = 0 or is “Undefined”
 SLOPE = 0: The graph of an equation such as y= (some value) is
always represented by a horizontal line and is commonly referred to as
20
a Constant Function. Since all points along a horizontal line have the
same value for the y-coordinate, the value of  y is always equal to
zero and as a result, the slope of this line is always zero (0).
EXAMPLE:
Graph the equation of a line that goes through the point (4, -3)
and has a slope of 0. What is the equation of this line?
10
8
6
4
2
-10 -8 -6 -4 -2
2
4
6
8 10
-2
-4
-6
-8
-10
 SLOPE = UNDEFINED: The graph of an equation such as
x= (some value) is always represented by a vertical line. Since all
points along a vertical line have the same x-coordinate, the value of
x is always equal to zero and as a result, the slope of this line is
always “Undefined.” An undefined slope is sometimes also described
as “No Slope” or is represented by the Greek symbol phi (  ).
EXAMPLE:
Graph the equation of a line that goes through the point (3, 2)
and has an undefined slope. What is the equation of this line?
10
8
6
4
2
-10 -8 -6 -4 -2
2
-2
-4
-6
-8
-10
21
4
6
8 10
8B. GRAPHING LINEAR EQUATIONS BY SLOPE AND Y-INTERCEPT
SLOPE-INTERCEPT FORM:
m = slope
y  mx  b where 
b = y-intercept
1) If the equation is not in the “slope-intercept” form of y = mx+b,
complete the necessary transformations to get it into this form.
2) The y-intercept is given by the value of b in the equation and is the
starting point for completing this graph. This point would be graphed
on the y-axis as the ordered pair (0, y-intercept).
3) The slope is given by the value of m and indicates the direction to
move away” from the y-intercept in a stepwise manner. Using the
y-intercept as a starting point, find a second point on the graph by
moving away from the y-intercept. Find one point on either side of
the y-intercept to confirm the trend indicated by slope.
4) Draw a straight line through y-intercept and constructed points.
EXAMPLE:
Graph:
2x  3y  6
Step 1: Convert to slope intercept form:
2x  3y 
2x
6
2x
Addition Property of Equality
 1
 1
  3y   2x  6   
3
3
2
y  x 2
3
.
Multiplication Property of Equality
Step 2: Identify the key graphing parameters and graph:
y-intercept:
Since b = 2. the y-intercept is located at (0, 2).
slope:
Since m =
x   3
y   2
Starting point is at
y intercept (0, 2)
y   2
2
3
, then “move away” from the y-
intercept starting point by moving 2 units
in the positive y direction and then 3 units
in the positive x direction. It could also
mean a move of 2 units in the negative y
direction and then 3 units in the negative
x direction since 23 = 23 .
x   3
22
REVIEW SECTION 9 – WRITING LINEAR EQUATIONS
While the slope intercept form of a linear equation, y  mx  b , is one of the
most convenient forms to use in order to easily graph a linear equation, the
point-slope form of a linear equation is the preferred format to use when
writing linear equations based on given information like slope of the line and
the coordinates of a solution point on the line.
The point-slope form of a linear equation is shown below:
 y  y1   m x  x1 
where : m
= slope
 x1 , y1  = coordinates of an ordered pair
on the line (and therefore, part
of solution set)
Upon careful examination, you will see that the point-slope form of a linear
equation is nothing more than an algebraic transformation of the slope
formula for a general value of x and y:
m
 y  y1  ;
 x  x1 
Cross multiply to obtain:
 y  y1   m x  x1 
9A. WRITING LINEAR EQUATIONS GIVEN A POINT AND A SLOPE
Example 1: Write the equation of a line that has a slope of 
through the point  3,  1)  .
Given : m  
3
;
4
x1  3;
y1   1
 y  y1   m  x  x1 
 y   1    34  x  3
3
9
x
4
4
3
9
y   x  1
4
4
3
5
y  x 
4
4
y 1  
23
3
and goes
4
9B. WRITING LINEAR EQUATIONS GIVEN TWO POINTS
Example 2: Write the equation of a line that goes through the points
 2, 5  and  6, 9  .
The only difference between this problem and the previous problem is that
slope has not been calculated for you. The starting point for this problem is
then to first find the slope of the line and then find the equation in the
same manner as demonstrated in the last example:
Given: x1   2
y1  5
Slope = m =
x2   6
y2   9
y
 y  y1     9   5   14  7
 2
x  x2  x1    6    2  
4
2
 y  y1   m  x  x1 
7
2
 y  5    x   2 
y 5 
7
x 7
2
7
x 7 5
2
7
y  x  12
2
y
24
9C. WRITING EQUATIONS FOR PARALLEL & PERPENDICULAR LINES
Parallel lines never intersect and therefore the slopes of these lines must be
equal. Perpendicular lines however, intersect at a 90 angle. The slopes of
perpendicular lines are negative reciprocals of each other.
Example 5:
3
2
The equation of a line is y  x  3 and therefore its slope is
The slope of a parallel line is therefore also
3
.
2
3
.
2
The equation of a line parallel to the original line is
y 
3
3
x  2 or y  x  13 etc ...
2
2
2
3
The slope of a perpendicular line is  .
The equation of a line perpendicular to the original line is
2
y   x  7 or
3
2
y   x  9 etc ...
3
1
3
Example 6: Find the equation of a line that is parallel to y  x  4 and goes
through the point (-3,7).
1
3
1
y  7   x  3
3
1
y 7  x 1
3
1
y  x 8
3
 y  7    x  (3) 
Slope is the same. Use
Point-Slope formula to
set up and transform to
Slope-Intercept form.
3
5
Example 7: Find the equation of a line that is perpendicular to y   x  4
and goes through the point (2,-9).
5
 y   9    3  x  2
5
10
x
3
3
5
10
y  x
9
3
3
5
37
y  x
3
3
y 9 
25
Slope is the negative reciprocal.
Use Point-Slope formula to
set up and transform to
Slope-Intercept form.
REVIEW SECTION 10 – SOLVING SYSTEMS OF EQUATIONS
Vocabulary: Two or more linear equations in the same variables represent a
system of linear equations or a linear system.
Three possible scenarios exist when solving a system of equations:
1) One unique ordered pair satisfies all of the equations
in the system; the solution is given by that ordered
pair, (a, b).
2) An infinite number of ordered pairs satisfy all of the
equations in the system. In this case, the graphs of
both equations are the same line.
3) No ordered pairs satisfy all of the equations; the
graphs of these equations are parallel and therefore
do not intersect. As a result, the system has no
solution, given by the Greek symbol .
If the solution to a system of linear equations in two variables is an
ordered pair of numbers (a, b), then substitution of this ordered pair
into either one of the equations in the system (x = a and y = b), results
in a true statement. The point (a,b) lies on the graph of each equation
and is the point of intersection of the graphs.
10A. SOLVING SYSTEMS OF EQUATIONS GRAPHICALLY
Example:
-3x + y = -7
2x + 2y = 10
Solution: Rewrite each equation in slope-intercept form.
1) -3x + y = -7
 y = 3x –7
Slope: 3
y int: (0. –7)
2) 2x + 2y = 10
 y = -x + 5
Slope: -1
y int: (0, 5)
Graph of Equation # 2
Graph of Equation # 1



26
Solution to system is given by
coordinates of intersection of
the two equations. In this case,
the solution is (3, 2)
10B. SOLVING SYSTEMS OF EQUATIONS BY LINEAR
COMBINATION (also known as Elimination)
The objective in this method is to get the coefficients of one variable
to be opposite numbers.
Example: Solve the system: 4x - 3y = 11
3x + 2y = -13
To eliminate the y
4x - 3y = 11
3x + 2y = -13
 Multiply by 2
 Multiply by 3
 8x - 6y = 22
 9x + 6y = -39
Add the equations 
Solve for x

17x
= -17
x = -1
Substitute - 1 for x in either of the original equations and solve for y.
3x + 2y = -13
3(-1) + 2y = -13
– 3 + 2y = -13
2y = -10
y = -5
Substitute –1 for x
Simplify
Add 3 to each side
Solve for y
The solution is ( -1 , -5 )
27
10C. SOLVING SYSTEMS OF EQUATIONS BY SUBSTITUTION
The method of solving systems by substitution should be considered
when at least one of the variables in the system has a coefficient of
one (1) as demonstrated in the following example:
Example:
x+y=1
2x –3y = 12
Solution: Solve for y in the first equation
y = -x + 1
Substitute –x + 1 for y in the second equation and solve for x.
2x – 3y = 12
2x – 3(-x + 1) = 12
2x + 3x – 3 = 12
5x – 3 = 12
5x = 15
x=3
Substitute –x + 1 for y
Distribute the –3
Combine like terms
Add 3 to each side
Divide each side by 5
Find the value of y by substituting 3 for x in an original equation.
3+y=1
y = -2
or
2(3) – 3y = 12
6 – 3y = 12
- 3y = 6
y = -2
28
Solution: ( 3, -2)
REVIEW SECTION 11 – INEQUALITIES IN TWO VARIABLES
AND SYSTEMS OF INEQUALITIES
11A. GRAPHING A LINEAR INEQUALITY IN TWO VARIABLES
Any point in shaded
region is a member of
the solution set.
Example: Graph x – y < 2
The corresponding equation is x – y = 2. In
slope-intercept form, this equation is y= x – 2.
Graph this line using a slope of 1 and y-intercept
of -2 . Use a dashed line to show that the points
on the line are not solutions since the original
inequality is just “  ”, not “  ”.
y
Test Point
(0, 0)
Use the coordinates of a point that is not on the
line to determine the region in which the original
inequality will be satisfied. For ease of calculation,
always consider using the origin (0,0) as the test
Points on line are
point unless it is on the line. Substituting the values of the
excluded from solution
set in this example
coordinates into the original inequality will generate either a
(dotted line).
true or false statement. In this example, (0,0) generates a
true statement (0 – 0 < 2 is true) and therefore, all points in the
region above the line (where the test point is located) are included in
the solution set. If the coordinates had generated a false statement,
then that region would be excluded from the solution set. This area is
then shaded to show the region of the graph representing the solution
set (i.e. the solution set for this inequality is the set of all points
above the graph of y = x – 2.
NOTE: The type of line used for the boundary between solution
points and non-solution points always depends on the type of inequality
presented in the original problem:
Inequality Symbol
 or 
 or 
“Boundary” line type
Dotted or dashed line
Solid line
29
REVIEW SECTION 12 – RULES OF EXPONENTS
Vocabulary
Power of a number: A product of equal factors. For example, 2  2  2 ,
means the third power of 2.
Base of a power: The number that is used as a factor. For example, 2 is
the base of 23 .
Exponent: In a power, the number that indicates how many times the base
is used as a factor. For example, 3 is the exponent in 23 .
Exponential form: The power of a number written using a base and an
exponent. The expression 23 is the exponential form of 2  2  2 .
Note: An exponent goes with the base immediately preceding it unless
parentheses indicate otherwise.
Example 1:
3y 2 means 3  y  y
2 is the exponent of the base y.
3y 
2 is the exponent of the base 3y.
2
means 3y  3y
Product of Powers: When two powers with the same base are multiplied,
add the exponents.
a m  a n  a m n
Example 2:
x 2  x 5  x 2 5  x 7
Think: x is being used as a
factor a total of 7 times.
Example 3:
32  33  323  35
Example 4:
6c  3c 5  6c 1  3c 5  6  3  c 15  18c 6
Power of a Power: When a power is raised to a power, multiply exponents.
a 
m n
Example 5:
x 
 x 76  x 42
Example 6:
2 
 234  212
7 6
3 4
 a mn
30
Power of a Product: When a product is raised to a power, raise each factor
to the power and then multiply.
ab 
5
Example 7:
 2x 
Example 8:
6x
2
m
 a mb m
5
  2 x 5  32x 5
y 5    6  x 2   y 5   216x 6y 15
3
3
3
3
Quotient of Powers: When two powers with the same base are divided,
subtract the exponents.
am
If m  n ,
 a m n
an
am
1
If n  m,
 n m
n
a
a
Example 9:
x8 x  x  x  x  x  x  x  x

 x8  5  x 3
5
x
x x x x x
Example 10:
x5
1
1
 8 5  3
8
x
x
x
Example 11:
Think: Where are the most factors of
x? How many extra factors?
4a 3b 2
a2


16ab 3
4b
Power of a Quotient: When a quotient is raised to a power, raise the
numerator and the denominator to that power. Then divide and simplify.
m
m
a   a
 
bm
b 
Example 12:
5
25
32
32
 2 




5
5
4 
20
 3x 
3x 4  35   x 4  243x
31
Zero Exponents: If a is a real number not equal to zero, then a 0  1 .
(The expression 0 0 has no meaning!)
Example 13:
250  1
Example 14:
5x 0  5  1  5
but
5x 
0
Remember: An exponent goes with the base
immediately preceding it, unless otherwise
indicated by parentheses.
1
Negative Exponents: If a is a nonzero real number and n is a positive
1
integer, then a n  n . Negative exponents mean reciprocals! All rules for
a
positive exponents also hold for negative exponents.
1
1

3
2
8
Note: Negative exponents do not mean
negative numbers!
Example 15:
23 
Example 16:
x 
Example 17:
2x 
Example 18:
x9
 x 9  x 2  x 11
2
x
Example 19:
x5
1
 x 512  x 7  7
12
x
x
Example 20:
4x 5
4x 5 3) 

 2x 8
3
2x
2
1 2
2 4
 x  1 2  x 2
 24   x 2   16x 8 
4
16
x8
Remember: An exponent goes with the base
immediately preceding it, unless otherwise
indicated by parentheses.
Note: The preferred form of a simplified expression
has only positive exponents.
32
REVIEW SECTION 13 – OPERATIONS WITH POLYNOMIALS
Vocabulary
Monomial: An expression that is either a numeral, a variable, or the product
of a numeral and one or more variables. Also called terms.
Examples: 13, m, 8c, 2xy, 5p 2q
Coefficient: In a monomial, the number preceding the variable. When a
monomial does not have a written coefficient, its coefficient is 1.
Polynomial: A sum of monomials. Example: x 2  3x  y 2  2
Binomial:
A polynomial that has exactly two terms. Example: 2x  5
Trinomial:
A polynomial that has three terms. Example: a 2  2ab  b 2
Similar or Like Terms: Two monomials that have exactly the same variable
names. Examples: 3xy and 7xy , 5ab 2 and ab 2
Addition of Polynomials: To add two or more polynomials, combine the
coefficients of the like-terms.
Example 1:
2x
2
 5xy  6y 2    8x 2  6xy  y 2   10x 2  11xy  5y 2
Subtraction of Polynomials: To subtract polynomials, change the second
polynomial to its opposite and then add to the first polynomial.
Example 2:
3x
3x
2
2
 6xy  2y 2  5    x 2  5xy  6y 2  3 
 6xy  2y 2  5    x 2  5xy  6y 2  3  4x 2  11xy  8y 2  2
Multiply a Polynomial by a Monomial: Multiply each term of the polynomial
by the monomial, apply the rules for exponents as appropriate.
Example 3:
2x 3x 2  2x  1   6x 3  4x 2  2x
33
Multiply a Binomial by a Binomial: Multiply each term of the first binomial
by each term of the second binomial using the distributive property. “FOIL”
(First times First, Outer product, Inner Product, Last times Last)
L
F
a  b  c  d 
I
O
Example 4:
3x
 22x  5   6x 2  15x  4x  10  6x 2  11x  10
Multiply a Polynomial by a Binomial: Use the distributive property twice
to multiply each term of the binomial times each term of the polynomial.
Then combine like-terms.
Example 5:
2x
 3  x 2  4x  5   2x 3  8x 2  10x
3x 2  12x  15
2x 3  11x 2  2x  15
Special Products:
Difference of Two Squares:
Squares of Binomials:
a  b a  b   a 2  b 2
2
a  b   a 2  2ab  b 2
2
a  b   a 2  2ab  b 2
Example 6:
2n  32n  3  4n 2  9
Example 7:
x
Example 8:
5x
Perfect Square
Trinomials
 4   x 2  2(x  4)  42  x 2  8x  16
2
2
2
2
 2  5x   2(5x  2)  2  25x 2  20x  4
34
REVIEW SECTION 14 – FACTORING POLYNOMIALS
Factoring polynomials – to write a polynomial as the product of polynomials of
lower degree. A polynomial with integral coefficients whose greatest
common factor is 1 and cannot be written as the product of polynomials of
lower degree is called prime. A polynomial is factored completely when each
polynomial factor is prime.
Guidelines for Factoring
1)
Factor out the greatest monomial factor, GCF, first! The greatest
monomial factor is the greatest coefficient and greatest degree of
each variable common to every term in the polynomial.
Example 1:
2)
The greatest monomial factor of 6x 5  4x 3  8x is 2x
since 6x 5  4x 3  8x  2x 3x 4  2x 2  4  .
Look for special patterns:
Difference of Squares:
a 2  b 2  a  b a  b 
The difference of squares is a binomial difference whose two factors
are perfect squares as its name suggests. To factor, take the square
root of each term and write as the product of the difference of the
square roots times the sum of the square roots.
Example 2a: 25x 2  121  5x  11 5x  11 
a 2  2ab  b 2  a  b 
2
Perfect Square Trinomial:
a 2  2ab  b 2  a  b 
2
To determine if a trinomial is a perfect square, both the first and last
terms should be perfect squares and the coefficient of the middle
term should be twice the product of the square roots of the first and
last terms disregarding the sign.
Example 2b: 4x 2  12x  9 is a perfect square trinomial because
2
2
2
4x 2  2x  , 9  3 and 12x  2 2x 3 so 4x 2  12x  9  2x  3 .
35
Example 2c: 16x 2  20x  25 is not a perfect square trinomial
Even though 16x 2 and 25 are perfect squares, the coefficient of the
middle term should be 2  4x  5  40x . This is a prime polynomial.
3)
If the polynomial is a trinomial that does not fit a special pattern,
look for a pair of binomial factors.
For x 2  bx  c , find two factors of c whose sum is b.
Example 3a: x 2  6x  8   x  2  x  4  since 2(4) = 8 and 2 + 4 = 6.
Note the following factoring patterns:
when b is positive:
 x  ? x  ?
when b is negative:
 x  ? x  ?
If c is positive
 x  ? x  ?
If c is negative:
Example 3b: Factor 10x 2  11x  3
Because the constant term is positive and the linear term is negative,
the factoring pattern will be  ? x  ? ? x  ?  . Find factors of 10x 2
and factors of 3; test to see which produces –11x as a linear term.
10x 2  11x  3  5x  32x  1 
36
REVIEW SECTION 14 – SOLVING QUADRATIC EQUATIONS
Quadratic equations have two solutions as compared to linear equations that
just have one solution. You can tell that an equation is quadratic if one of
the variable terms is squared (i.e. of 2nd degree). We will be exploring a
number of different methods for solving quadratic equations in Algebra 2H.
You have already used one of these methods which is called the Factoring
and Zero Product Property method.
Factoring and Zero Product Property
In the event that a quadratic equation has quadratic (squared) and linear
terms (raised to the 1st power), factoring by GCF, Difference of Squares or
Trinomial Factoring methods along with the use of the Zero Product
Property allows easy determination of the solutions.
Example 1: Solve
Example 2: Solve
x2  6x  8  0
( x  4)( x  2)  0
x  4  0 or x  2  0
x  4 or
x2
Factor
Zero Product Property
Set each factor = 0
and solve.
3x3  12 x  0
 3x   x 2  4   0
 3x  x  2  x  2   0
Factor (GCF)
Factor (Diff of Sq.)
Zero Product Property
3x  0 or x  2  0 or x  2  0
Set each factor = 0
x  0 or
x  2 or x  2
and solve.
Example 3: Solve
49 x 2  100  0
(7 x  10)(7 x  10)  0
7 x  10  0 and 7 x  10  0
10
10
x
and
x
7
7
Example 4: Solve
0
2 x2  x 1  0
(2 x  1)( x  1)  0
2 x  1  0 and x  1  0
1
x
and
x 1
2
37
Factor (Diff of Sq.)
Zero Product Property
Set each factor = 0
and solve.
Factor
Zero Product Property
Set each factor =
and solve
REVIEW SECTION 15- RADICAL EXPRESSIONS
Radical Expression: An expression of the form a . The symbol, , is
called a radical sign and the expression under the radical sign, “a”, is called
the radicand.
Square root: If a 2  b , then a is a square root of b.
(Note: Negative numbers do not have square roots in the set of real
numbers.)
Symbols:
64  8
 64  8
indicates the nonnegative or principal square root of 64
indicates the negative square root of 64
 64  8 indicates both square roots of 64
I. Simplifying Radicals: To simplify a radical expression, find the square
root of any factors of the radicand that are perfect squares. (If you cannot
see any squares, you can use prime factorization of the radicand.)
Product Property of Square Roots
For any nonnegative real numbers a and b:
ab  a  b
Example:
49  4  9
Quotient Property of Square Roots
For any nonnegative real number a and any positive real number b:
a
a

b
b
Example:
Example 1:
256  4  64  4  64  2  8  16
Example 2:
50  25  2  25  2  5  2  5 2
Example 3:
Example 4:
2 80  2 16  5  2  4 5  8 5
169
169 13


100
100 10
38
36
36

4
4
II. Multiplying Radicals:
Example 5:
4 2  3  4 23  4 6
Example 6:
2 3  3 48  2  3  3  48  6 144  6  12  72
III. Dividing Radicals:
Example 7:
7 54
7 54




6 28
6 28
9 3

4 2
Example 8:
24 33
12 33



 18  3 2
11
2
11 2
IV. Rationalizing Denominators: A radical is not considered to be in simplest
form if there is a fraction under the radical sign or a radical in the
denominator. Rationalizing is the process of eliminating a radical from the
denominator. (Remember:
 a
2
a)
Example 9:
1
1
1
3
3




3
3
3
3 3
Example 10:
5
5
2 5 2



2
2
2 2
V. Adding and Subtracting Radicals: Only radicals with like radicands can be
combined.
Example 11:
8  18  4  2  9  2  2 2  3 2  5 2
Example 12:
6  24  6  4  6  6  2 6   6
39
REVIEW SECTION 16 – LINEAR & QUADRATIC
APPLICATIONS
Problem Solving Process
Explore the Problem
Read the problem and identify what is given and what is asked. Jot down
important facts from the problem. Sometimes it is helpful to draw a chart
or diagram. Think about how the facts are related.
Plan the solution
Many different strategies may be used. If an equation will be used to solve
the problem, read the problem again. Decide how the unspecified numbers
relate to other given information. Write an equation to represent the
relationship, making sure to identify the variables.
Solve the problem
This involves doing the mathematics and interpreting the answer. If an
equation was written, solve the equation and interpret the solution. State
the answer to the problem in words (e.g. an answer is 13 cm, not just 13).
Examine the solution
Check whether the answer makes sense with the conditions of the problem.
If not, check your math again – sometimes, silly arithmetic mistakes are the
cause. If the math is correct, then a mistake was made in “setting up” the
problem. If this is the case, explore the problem again and try a different
approach.
Remember that not all problems in real life can be solved by using an
equation. Sometimes there is no “clear-cut” method of solution. Thus, it is
important to realize that there may be alternative strategies for solving
problems. The four-step problem solving plan outlined above can be used to
solve any type of problem using any strategy.
Problem
1.
2.
3.
4.
5.
6.
7.
8.
9.
Solving Strategies
Draw a picture or diagram
Make an organized, exhaustive list
Make a chart or table
Look for a pattern
Write an equation
Work backwards
Solve a simpler form of the problem
Simulate a problem
Make a guess, then check
40