Download Absolute Value - Garnet Valley School District

Absolute Value
A. Evaluating Expressions with Absolute Value in Them
1. Absolute values are done (if possible) as if their contents were in parentheses.
(Evaluate the inside first, then apply absolute value)
Ex: valuate each of the following if x = 2, y  
 3x 
yz  x
2
3
and z = 10
5
 x  ( z )
B. Solving Absolute Value Equations
1. To solve equations involving absolute value, get | something | = #
a. If the number is positive, split the equation in two cases.
Ex: Solve: 2 x  5  15
2 3x 1  6  14
b. If the number is negative, it is a trick question, there are no solutions.
Ex: Solve: 2 x  10
12  x  7  2
C. Solving Absolute Value Inequalities
1. Get | something | (inequality) #. Then do one of the following.
a. Split inequality in two cases using definition of absolute value.
1
x 6
3x  5  12  17
2
b. Take advantage of the limited types of problems in Algebra IIA to go
right to an “and/or” inequality.
2
1
x 4
10  2 x  12
3
2
Functions, Domain and Range
1. Graphs of Functions – Use the vertical line test to see if a graph depicts a function or
not. If there is a vertical line that hits the graph twice, the graph is not a function.
Determine (yes or no) whether the graph depicts a function.
6
4
2
-5
5
10
-2
-4
2. Domain and range and “Is it a function?” for a set of points.
A. Domain and range of a set of points. Domain is a list of x’s; range is a list of y’s.
Ex: Find domain and range of {(2, 1), (4, -2), (4, 7), (3, 6)}. Then determine whether or
not the set of points is a function. Explain why or why not.
3. Function notation, composite functions.
A. Function notation, like f(x) = 3x – 7 lets us know what to plug in for x in a
way that was different than we were used to.
If f ( x)  4 x, g ( x)  3x  8, and h( x)  x  4 ,
1. Find f(4)
2. Give x if h(x) = 18
4. Find f(g(x))
Given the function
5. Find m(4).
3. Find f(g(5))
x
m( x )
2 0
4
2
4
1 2 5
6. If m(x) = 4, find x.
Equations of Lines
A. Graphing
a. Using slope-intercepts form
b. Using point-slope form
c. Using x and y intercepts – Plug in x = 0 to find y value of y intercept; plug
y = 0 to find x value of x intercept. Plot the two points, draw line.
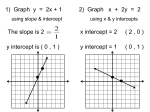
Find x and y intercepts of each. Then draw a graph.
1
3
 x y 6
2x – 3y = -6
3
4
d. Non-linear equations. Equations with any of the following are not straight
lines, and will need more than two points to determine
the graph.
1. Exponents greater than 1
2. Product of variables
3. Division by a variable.
Ex: Graph: y = x 2
y  x2  4
e. Equations with just one variable are horizontal or vertical lines.
Ex: Give the slope, y intercept and x intercept of each. Then graph.
x=4
2y – 8 = -10
B. Writing Equations of Lines
1. Choose from the following. Fill in the bold symbols with information from the
question.
Point-slope: y  y1 = m(x - x1 )
Horizontal line:
(slope = 0)
y=#
Slope-intercept: y = mx + b
Vertical Line: x = #
(No slope or undefined slope)
2. Write the equation of the lines described.
a. Passes through (0, 3) and (4, 6)
b. Passes through (-2, 4) with slope
of 2.
c. Passes through (3, 5) and (3, 12)
d. Passes through (2, 5) x intercept = 4.
2. Parallel lines have the same slope, perpendicular lines have slopes that are
opposite reciprocals.
a. Write the equation of the line parallel to -2y + x = 2 and passing through (3, 6)
1
x  2 y  1 and passing
3
through (0, -6). Give answer in slope intercept form.
b. Write the equation of the line perpendicular to
3. Hiring a plumber for a 4 hour job costs $120, and hiring them for a 7 hour job
costs $195. Assuming their pay is a linear function of the hours they work,
write the equation for the situation. Then determine what they would be paid
for 12 hours of work.