* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Physics Oration - Part 1
Abraham–Minkowski controversy wikipedia , lookup
Magnetic monopole wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
James Clerk Maxwell wikipedia , lookup
Faraday paradox wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Maxwell's equations wikipedia , lookup
Variable speed of light wikipedia , lookup
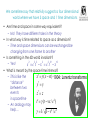
STAV & AIP VCE Physics Teachers’ Conference, Feb 17 2006 Physics Oration S: 37o 54.807’, E: 145o 07.940’ Questions about Einstein’s Relativity Answered Prof David N. Jamieson School of Physics University of Melbourne Einstein in 1905 Where did the Special Theory of Relativity come from? • He seems to have been fascinated from an early age by the nature of light, a fascination that persisted throughout his life • From an essay he wrote in 1895, (at age 16), we know that he then believed in the ether, and had heard of Hertz's experiments on the propagation of electromagnetic waves; but he does not show any knowledge of Maxwell's theory • In much later reminiscences, he reports that during the following year (1895-1896) he conceived of a thought experiment: what would happen if an observer tried to chase a light wave? Could s/he catch up with it? If so, s/he ought to see a non-moving light wave form, which somehow seemed strange to him • In retrospect, he called this "the first childish thoughtexperiment that was related to the special theory of relativity This is from the text of "'What Song the Syrens Sang': How Did Einstein Discover Special Relativity?" as printed in John Stachel, Einstein from "B" to "Z" (Boston : Birkhäuser, 2002), pp. 157-169. Can you catch a beam of light? Mysterious Magnetism How does a compass work? Two ways to make electricity! S N Changing magnetic field makes and ELECTRIC field Achtung!: There does not need to be two laws of Physics here! S N Moving charge in wires feels MAGNETIC force What was the basic problem that Einstein was concerned with pre 1905? • Moving magnet is changing flux – Faraday Law of Induction makes electrons move d B E.d s dt loop • Moving coil is moving electrons – Magnetic force makes electrons move FM qv B Galileo: Can’t have a velocity dependent force in mechanics! The F=qvB force appeared to contradict the principle of inertia • Comments on his apparent lack of knowledge of the Michelson-Morley experiment – Einstein did not appear to know about it in 1905 • The implications of Maxwell’s equations Galileo 1634 The laws of Physics do not depend on absolute motion Does this include electromagnetism? YES! Maxwell 1873 The great treatise of electromagnetism Electromagnetic fields and waves propagate through the Aether The Maxwell Equations do not have a place to insert the relative motion of source and observer Trouton Noble Experiment (1903) FM + Or ? + + 1 qq FE rˆ 2 4o r FE + FE FM • • • • + + v + + v v • • Current, • • i x +x x x v B x x x x FM qv B The (1905) paper was on the “electrodynamics of moving bodies” • At first glance that doesn’t seem to make sense – moving bodies don’t have electromagnetic fields do they? – Yes! Even Lorentz knew matter was made of electrons and ions (by 1904) • Does the Lorentz contraction occur in empty space? – Yes! It arises from the relativity of simultaneity – even in empty space • What was meant by that title? – New forces (magnetism) arise from a moving charge • The full implications of the principle of relativity: His intuition that magnetic force was really electric force etc. “What led me more or less directly to the Special Theory of Relativity was the conviction that the electromotive force acting on a body in motion in a magnetic field was nothing else but an electric field.” A. Einstein (1952), from a letter to the Michelson Commemorative Meeting of the Cleveland Physics Society, quoted by R.S. Shankland, Am. J. Phys., 32, 16 (1964), p35. How did Einstein come to the two postulates? • Significance of Maxwell’s work, rather than MM expt. etc. – First postulate: Laws of Physics are the same in all reference frames • This is an affirmation of Galileo now stated to apply to all laws (mechanics and electromagnetism) – Second Postulate: Speed of light is independent of the speed of the source and the observer • This flows directly from the Maxwell equations! • Idea that the universe worked on ‘elegant’ principles (like relativity) – Not everyone agreed relativity was elegant! – F=ma is elegant, but not relativistically correct The Lorentz transformations • Why had Lorentz proposed them earlier? – From the invariance of the Maxwell equations – see next slide! • Was it to explain the MM expt? – No! Fitzgerald proposed the length contraction to explain MM then appealed to Oliver Heaviside to provide a mechanism – Heaviside’s derivation of the electric field of a moving charge particle revealed Special Relativity BEFORE Einstein but did not understand the implications. • And why does Einstein get all (well most of) the credit? – It was Einstein who linked the Lorentz transforms to the invariance of light and thereby uncovered the second postulate never before discovered by ANYONE else! The Maxwell Equations I Gauss’ Law for electrostatics q E.dA closed surf ace II Gauss’ Law for magnetism o B.dA 0 closed surf ace III IV Faraday’s Law of induction d B E.d s dt loop Ampere-Maxwell Law d E loopB.ds oi o o dt Predict the speed of light as an electromagnetic wave c 1 o o Magnetic fields during charging of a capacitor y y E Ex ( x, y, z )xˆ E y ( x, y, z )yˆ Ez ( x, y, z )zˆ v B Bx ( x, y, z )xˆ By ( x, y, z )yˆ Bz ( x, y, z )zˆ x x Simulation from Maxwell The Lorentz Transformations • Can use Maxwell equations to find: E Ex ( x, y, z )xˆ E y ( x, y, z )yˆ Ez ( x, y, z )zˆ B Bx ( x, y, z )xˆ By ( x, y, z )yˆ Bz ( x, y, z )zˆ • It was also found by Lorentz that the Maxwell equations were invariant under the transformations: x ( x vt) 1904: Lorentz transforms y y z z t (t vx / c 2 ) 1/ 1 v2 / c2 The significance of this was unknown to 19th C Physics! We sometimes say that relativity suggests a four dimensional world where we have 3 space and 1 time dimensions • Are time and space in some way equivalent? – No! They have different roles in the theory • In what way is time related to space as a dimension? – Time and space dimensions can be exchanged be changing from one frame to another • Is something in the 4D world invariant? – Yes! s 2 c 2t 2 x 2 c 2t 2 x2 • What is meant by the space-time interval? x ( x vt) 1904: Lorentz transforms – This is like the “distance” y y between two events z z in spacetime t (t vx / c 2 ) – An analogy may help… 1/ 1 v2 / c2 Maps of space N E