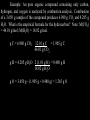Download Chapter 8

CHAPTER 8
Chemical Reactions
Dalton’s Atomic Theory
We have previously discussed Dalton’s atomic theory.
1) Matter is composed of small indivisible particles called atoms.
All atoms of a particular elements are identical. Atoms of different
elements differ in their chemical and physical properties. (Chapter 2).
2) Compounds are composed of molecules. Each molecule
contains the same number of atoms of each element making up the
compound. (Chapter 5).
3) In a chemical reaction atoms are rearranged, but atoms are
neither created, destroyed, or converted from atoms of one element to
atoms of another element.
We are now ready to discuss the last concept in Dalton’s theory,
the rearrangement of atoms in a chemical reaction.
Balanced Chemical Equation
A balanced chemical equation indicates the starting substances
(reactants) and ending substances (products) of a chemical reaction. The
reactions may also indicate the state of the reactants and products, and/or
the physical process used in the reaction.
s = solid
 = liquid
g = gas
aq = aqueous
 = heat
A balanced equation must satisfy conservation of mass (same
number of atoms of each element on the reactant and product side) and
conservation of electrical charge (same total charge on the reactant and
product side). This means that chemical reactions must be consistent
with Dalton’s theory.
Examples of Balanced Chemical Equation
Combustion of hydrogen (combustion is the reaction of a
substance with molecular oxygen to form combustion products).
2 H2(g) + O2(g)  2 H2O()
Nitration of toluene to form trinitrotoluene (TNT)
C6H5CH3 + 3 HNO3  C6H2CH3(NO2)3 + 3 H2O
Decomposition of calcium carbonate (decomposition is the
breakdown of a single reactant into two or more products).
CaCO3(s)

CaO(s) + CO2(g)
Dissolution of potassium sulfate, an ionic compound, in water.
K2SO4(s)
H2O
2 K+(aq) + SO42-(aq)
Procedure For Balancing Chemical Equations
1) Begin with a complete set of reactants and products. These
cannot be changed.
2) Find a set of numbers (stoichiometric coefficients) that satisfy
mass balance.
a) Change the coefficients of compounds before changing the
coefficients of elements (save elements for last in balancing).
b) Treat polyatomic ions that appear on both sides of the equation
as a unit.
c) Count atoms and polyatomic ions carefully, and track them
every time you change a coefficient.
Procedure For Balancing Chemical Equations
3) Convert the stoichiometric coefficients into the smallest set of
whole numbers that correctly balance the chemical equation.
1/
2
N2 + 3/2 H2  NH3
incorrect; fractional coefficient
N2 + 3 H2  2 NH3
correct
2 N2 + 6 H2  4 NH3
incorrect; not smallest set of whole
numbers
This step can be saved for last. Remember that if a chemical equation is
correctly balanced then multiplying all of the coefficients by the same
number results in an equation that is also balanced.
There are a few cases where we do sometimes use fractional
coefficients to balance chemical equations because of how the reaction is
defined, as will be discussed.
Example - Combustion of Iso-octane
Balance the following unbalanced chemical equation for the combustion of iso-octane, a hydrocarbon used to determine the octane rating
of gasoline
C8H18 + O2  CO2 + H2O (unbalanced)
Example - Combustion of Iso-octane
unbalanced
C8H18 + O2  CO2 + H2O
balance for C
C8H18 + O2  8 CO2 + H2O
balance for H
C8H18 + O2  8 CO2 + 9 H2O
balance for O
C8H18 + 25/2 O2  8 CO2 + 9 H2O
convert to whole numbers (multiply through by 2)
2 C8H18 + 25 O2  16 CO2 + 18 H2O
Example - Precipitation of Lead (II) Chloride
Precipitation reaction - A reaction where two soluble compounds
are mixed and a solid product is formed.
Pb(NO3)2(aq) + NaCl(aq)  PbCl2(s) + NaNO3(aq) (unbalanced)
Example - Precipitation of Lead (II) Chloride
unbalanced
Pb(NO3)2(aq) + NaCl(aq)  PbCl2(s) + NaNO3(aq)
balance for Cl
Pb(NO3)2(aq) + 2 NaCl(aq)  PbCl2(s) + NaNO3(aq)
Balancing for Cl has now caused the above reaction to be unbalanced for Na. So we go back and rebalance for Na
Pb(NO3)2(aq) + 2 NaCl(aq)  PbCl2(s) + 2 NaNO3(aq)
The above is now balanced.
Remember that when you have a cation or anion group (such as
NO3- above) it is often easier to balance equations treating this group as a
unit.
Types of Chemical Reactions
There are literally thousands of different types of chemical
reactions. Three common types are:
Combination reaction - Two or more reactants form a single
product.
H2(g) + Cl2(g)  2 HCl(g)
Decomposition reaction - A single reactant forms two or more
products.
CuSO4 • 5 H2O(s)

CuSO4(s) + 5 H2O(g)
Combustion reaction - Reaction of a single substance with
molecular oxygen to form combustion products (CO2(g), H2O()).
C3H8(g) + 5 O2(g)  3 CO2(g) + 4 H2O()
Combustion Analysis
Combustion analysis is a method often used in the analysis of
organic compounds. A sample of the compound is allowed to completely
react with oxygen and the mass of carbon dioxide (CO2) and water (H2O)
produced is measured. From this information the number of grams and
the number of moles of carbon and hydrogen originally in the sample can
be found.
Combustion Analysis (Hydrocarbons)
Combustion analysis can be carried out for hydrocarbons
(compounds containing only carbon and hydrogen). This is because all
of the carbon originally present in the compound is converted into CO2,
and all of the hydrogen is converted into H2O.
Example:
C8H16 + 12 O2  8 CO2 + 8 H2O
By knowing the mass of carbon dioxide and water formed by
combustion, the mass and moles of carbon and hydrogen in the original
compound can be found. From this, the empirical formula can be
determined.
Combustion analysis can also be carried out on organic
compounds that contain C, H, and O, as the same two combustion
products will form as with hydrocarbons.
Example:
2 CH3CHO + 5 O2  4 CO2 + 4 H2O
Example: A pure hydrocarbon is analyzed by combustion
analysis. Combustion of a sample of the hydrocarbon produces 3.65 g
CO2 and 1.99 g H2O. What is the empirical formula for the
hydrocarbon? Note: M(CO2) = 44.01 g/mol; M(H2O) = 18.02 g/mol.
Example: A pure hydrocarbon is analyzed by combustion
analysis. Combustion of a sample of the hydrocarbon produces 3.65 g
CO2 and 1.99 g H2O. What is the empirical formula for the
hydrocarbon? Note: M(CO2) = 44.01 g/mol; M(H2O) = 18.02 g/mol.
moles C = 3.65 g CO2 1 mol CO2 1 mol C = 0.0829 mol C
44.01 g CO2 1 mol CO2
moles H = 1.99 g H2O 1 mol H2O 2 mol H = 0.221 mol H
18.02 g H2O 1 mol H2O
relative moles C = 0.0829 mol/0.0829 mol = 1.00
relative moles H = 0.221 mol/0.0829 mol = 2.67
To get values close to integers multiply by 3.
Empirical formula = C3H8
(3.00)
(8.01)
Combustion Analysis (C, H, and O Present)
For a compound containing carbon, hydrogen, and oxygen,
combustion analysis is more complicated. That is because some of the
oxygen in the combustion products comes from the compound, and some
of the oxygen comes from the O2 used to carry out the combustion.
Example:
C6H12O6 + 6 O2  6 CO2 + 6 H2O
While all of the carbon and hydrogen in the combustion products comes
from the original compound, some of the oxygen comes from the
molecular oxygen used to carry out the combustion reaction.
Combustion Analysis (C, H, and O Present)
To do combustion analysis for a compound in this case requires
knowing the total mass of compound burned. Since
mtotal = mC + mH + mO
Then
mO = mtotal – (mC + mH)
The grams (and moles) of carbon and hydrogen present in the compound
are found as before. We can then use the above equation to find the
grams and moles of oxygen, and, from that, the empirical formula for the
compound.
Example: An pure organic compound containing only carbon,
hydrogen, and oxygen is analyzed by combustion analysis. Combustion
of a 3.650 g sample of the compound produces 6.980 g CO2 and 4.285 g
H2O. What is the empirical formula for the hydrocarbon? Note: M(CO2)
= 44.01 g/mol; M(H2O) = 18.02 g/mol.
Example: An pure organic compound containing only carbon,
hydrogen, and oxygen is analyzed by combustion analysis. Combustion
of a 3.650 g sample of the compound produces 6.980 g CO2 and 4.285 g
H2O. What is the empirical formula for the hydrocarbon? Note: M(CO2)
= 44.01 g/mol; M(H2O) = 18.02 g/mol.
g C = 6.980 g CO2
12.01 g C = 1.905 g C
44.01 g CO2
g H = 4.285 g H2O 2 (1.01 g H) = 0.480 g H
18.02 g H2O
g O = 3.650 g - (1.905 g + 0.480 g) = 1.265 g O
mol C 1.905 g C 1 mol C = 0.1586 mol C
12.01 g C
mol H = 0.480 g H 1 mol H = 0.475 mol H
1.01 g H
mol O = 1.265 g O
1 mol O = 0.07906 mol O
16.00 g O
Relative moles
C
0.1586 mol/0.07906 mol = 2.006
H
0.475 mol/0.07906 mol = 6.01
O
0.07906 mol/0.07906 mol = 1.000
So the empirical formula is C2H6O.
Interpretation of Chemical Equations
Consider the equation for the formation of water from hydrogen
and oxygen (note that this is both a combustion reaction and a
combination reaction).
2 H2(g) + O2(g)  2 H2O()
We can interpret this equation in two ways:
1) Two molecules of hydrogen and one molecule of oxygen
combine to form two molecules of water.
2) Two moles of hydrogen and one mole of oxygen combine to
form two moles of water.
Note that the second interpretation makes sense even if we have
fractional stoichiometric coefficients.
One of the most important uses of a balanced chemical equation
is to provide the information needed to convert from the amount of one
substance involved in a reaction and the amount of a second substance
that is required for the reaction.
Example: Consider the following balanced chemical equation
2 H2(g) + O2(g)  2 H2O()
If we begin with 4.8 moles of H2, how many moles of O2 will be
required for a complete reaction? What is the maximum number of
moles of H2O that we will be able to produce?
Example: Consider the following balanced chemical equation
2 H2(g) + O2(g)  2 H2O()
If we begin with 4.8 moles of H2, how many moles of O2 will be
required for a complete reaction? What is the maximum number of
moles of H2O that we will be able to produce?
mol O2 = 4.8 mol H2 1 mol O2 = 2.4 mol O2
2 mol H2
mol H2O = 4.8 mol H2 2 mol H2O = 4.8 mol H2O
2 mol H2
Example:
reaction occurs.
When sodium metal is placed in water a violent
2 Na(s) + 2 H2O()  2 NaOH(aq) + H2(g)
If we begin with 4.0 moles of sodium metal, how many moles of
water are required to completely react with the sodium metal? How
many moles of hydrogen gas will form?
2 Na(s) + 2 H2O()  2 NaOH(aq) + H2(g)
If we begin with 4.0 moles of sodium metal, how many moles of
water are required to completely react with the sodium metal? How
many moles of hydrogen gas will form?
mol H2O = 4.0 mol Na 2 mol H2O = 4.0 mol H2O
2 mol Na
mol H2 = 4.0 mol Na 1 mol H2 = 2.0 mol H2
2 mol Na
Calculations Using Mass of Reactants and Products
In the laboratory we work with masses of reactants and products.
However, as we have seen, chemical equations give relationships among
moles of reactants and products. We therefore need a method for going
back and forth between moles of substance and grams of substance.
We may do this conversion using M, the molecular mass or
formula mass of a substance. For example, the molecular mass of ethane
(C2H6) is
M(C2H6) = 30.07 g/mol
This is a conversion factor between mass of C2H6 and moles of
C2H6.
Strategy For Calculations Using Balanced Chemical
Equations
We may use the following strategy to find the mass of reactant or
product in a chemical equation.
1) Convert from grams of the first substance into moles of the
first substance using the molecular mass of the substance.
2) Use the balanced chemical equation to find the correct number
of moles of the second substance.
3) Convert from number of moles of the second substance to
mass of the second substance using the molecular mass of the substance.
Example
We can use a balanced chemical equation and our new concept of
moles to do calculations involving chemical reactions.
Example: Calcium chloride (CaCl2) can be produced by the
reaction of hydrochloric acid (HCl) and calcium hydroxide (Ca(OH)2).
2 HCl + Ca(OH)2  CaCl2 + 2 H2O
In a particular reaction we begin with 10.00 g HCl. How many
grams of Ca(OH)2 are required to completely react with this amount of
HCl? How many grams of calcium chloride can be produced by the
reaction?
calcium chloride
2 HCl + Ca(OH)2  CaCl2 + 2 H2O
In a particular reaction we begin with 10.00 g HCl. How many
grams of Ca(OH)2 are required to completely react with this amount of
HCl? How many grams of calcium chloride can be produced by the
reaction?
M(HCl) = 36.46 g/mol
M(CaCl2) = 110.98 g/mol
M(Ca(OH)2) = 74.09 g/mol
M(H2O) = 18.02 g/mol
1) Find the moles of HCl.
n(HCl) = 10.00 g HCl 1 mol HCl
36.46 g HCl
= 0.2743 mol HCl
2) Find the moles Ca(OH)2.
n(Ca(OH)2) = 0.2743 mol HCl 1 mol Ca(OH)2 = 0.1371 mol Ca(OH)2
2 mol HCl
3) Find the grams of Ca(OH)2
m(Ca(OH)2) = 0.1371 mol Ca(OH)2 74.09 g Ca(OH)2 = 10.16 g
1 mol Ca(OH)2
We can also find the mass of calcium chloride that can be
produced by the reaction
m(CaCl2) = 0.2743 mol HCl 1 mol CaCl2 110.98 g CaCl2
2 mol HCl
1 mol CaCl2
= 15.22 g CaCl2
Yields For a Chemical Reaction
There are three types of yields we can define for a chemical
reaction.
Theoretical yield - The maximum amount of product that can be
formed from the starting materials used in the reaction.
Actual yield - The observed yield for a chemical reaction.
Percent yield - The percent of the theoretical yield that is actually
obtained.
. 100%
% yield = actual yield
theoretical yield
For example, if the amount of CaCl2 actually obtained in the above
reaction was 11.46 g, then the percent yield for the reaction would be
% yield = 11.46 g . 100% = 75.3 %
15.22 g
Limiting Reactant
In most chemical reactions several reactants combine to form
products. As soon as one of the reactants runs out, the reaction will stop,
even if the other reactants are still present.
We define the limiting reactant as the reactant the first runs out in
a chemical reaction. Note that the theoretical yield of product is
determined by the limiting reactant.
Example: Consider making sandwiches out of cheese and bread.
One sandwich consists of two slides of bread and one slice of cheese. If
we begin with 10 slices of bread and 3 slices of cheese, what is the
“limiting reactant” and the “theoretical yield” of cheese sandwiches?
2 slices bread + 1 slice cheese  1 cheese sandwich
Start with
10 slices bread
3 slices cheese
“limiting reactant” = cheese
“theoretical yield” = 3 sandwiches
“excess reactant” = bread
Example: Methane can be formed by reacting carbon and hydrogen. If
we begin with 3 carbon atoms and 10 hydrogen molecules, what is the
limiting reactant, the excess reactant, and the theoretical yield of
methane? The balanced equation is C + 2 H2  CH4
limiting reactant = carbon
excess reactant = hydrogen
theoretical yield = 3 methane molecules
Note this works equally well if done in terms of moles.
Finding the Limiting Reactant
For a reaction involving two reactants (A and B) the limiting
reactant can be found as follows.
1) Find the number of moles of A and B.
2)
a) Find the number of moles of product that can be
formed from reactant A, assuming it is the limiting reactant
b) Find the number of moles of product that can be
formed from reactant B, assuming it is the limiting reactant
3) Whichever number of moles of product is smallest corresponds
to the limiting reactant. The other reactant is in excess. The smallest
number of moles corresponds to the theoretical yield of product.
The advantage of the above process is that it works no matter how many
reactants there are in the reaction.
Example: Consider the following chemical reaction (molecular
masses are given below each reactant).
C2H2
(26.04 g/mol)
+
2 HCl

(36.46 g/mol)
C2H4Cl2
(98.96 g/mol)
In a particular experiment we begin with 10.00 g C2H2 and 20.00 g HCl.
What is the limiting reactant and the theoretical yield of C2H4Cl2?
C2H2
(26.04 g/mol)
+
2 HCl

(36.46 g/mol)
C2H4Cl2
(98.96 g/mol)
In a particular experiment we begin with 10.00 g C2H2 and 20.00 g HCl.
What is the limiting reactant and the theoretical yield of C2H4Cl2?
moles C2H2 = 10.00 g 1 mol = 0.3840 mol C2H2
26.04 g
moles HCl = 20.00 g 1 mol = 0.5485 mol HCl
36.46 g
Moles C2H4Cl2 that could be produced if C2H2 is limiting
moles C2H4Cl2 = 0.3840 mol C2H2 1 mol C2H4Cl2 = 0.3840 mol
1 mol C2H2
Moles C2H4Cl2 that could be produced in HCl is limiting
moles C2H4Cl2 = 0.5485 mol HCl 1 mol C2H4Cl2 = 0.2743 mol
2 mol HCl
The smallest number of moles corresponds to HCl. Therefore:
HCl is the limiting reactant
C2H2 is in excess
The theoretical yield of C2H4Cl2 is 0.2743 mol
We can now use the molecular mass of C2H4Cl2 to convert the theoretical yield into grams of product.
theoretical yield (grams) =
0.2743 mol C2H4Cl2
98.96 g C2H4Cl2 = 27.14 g C2H4Cl2
1 mol C2H4Cl2
End of Chapter 8
“I have lived much of my life among molecules. They are good
company.” - George Wald
“The most exciting phrase to hear in science, the one that heralds
new discoveries, is not Eureka! (I found it!) but rather, ‘hmm.... that's
funny.…’” - Isaac Asimov
“…it has become hard to find an important problem (in science)
that is not already being worked on by crowds of people on several
continents.” - Max Perutz
“Not everyone learns from books.”
- Sheila Rowbothum, Resistance and Revolution