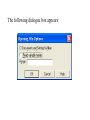
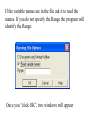
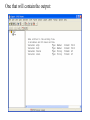
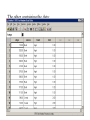
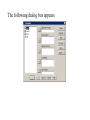
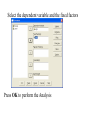
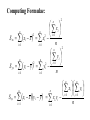
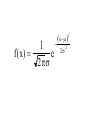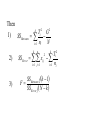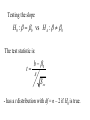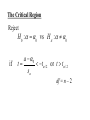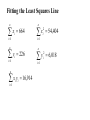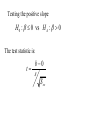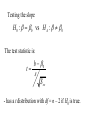* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Introduction - The Department of Mathematics & Statistics
Survey
Document related concepts
Transcript
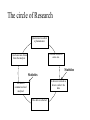
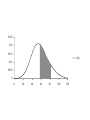
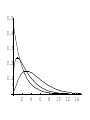
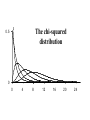
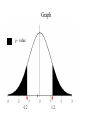
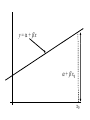
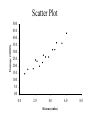
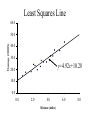
Stats 845 Applied Statistics This Course will cover: 1. Regression – – Non Linear Regression Multiple Regression 2. Analysis of Variance and Experimental Design The Emphasis will be on: 1. Learning Techniques through example: 2. Use of common statistical packages. • • • • SPSS Minitab SAS SPlus What is Statistics? It is the major mathematical tool of scientific inference - the art of drawing conclusion from data. Data that is to some extent corrupted by some component of random variation (random noise) An analogy can be drawn to data that is affected by random components of variation to signals that are corrupted by noise. Quite often sounds that are heard or received by some radio receiver can be thought of as signals with superimposed noise. The objective in signal theory is to extract the signal from the received sound (i.e. remove the noise to the greatest extent possible). The same is true in data analysis. Example A: Suppose we are comparing the effect of three different diets on weight loss. An observation on weight loss can be thought of as being made up of two components: 1. A component due to the effect of the diet being applied to the subject (the signal) 2. A random component due to other factors affecting weight loss not considered (initial weight of the subject, sex of the subject, metabolic makeup of the subject.) random noise. Note: that random assignment of subjects to diets will ensure that this component will be a random effect. Example B In this example we again are comparing the effect of three diets on weight gain. Subjects are randomly divided into three groups. Diets are randomly distributed amongst the groups. Measurements on weight gain are taken at the following times - one month - two months - 6 months and - 1 year after commencement of the diet. In addition to both the factors Time and Diet effecting weight gain there are two random sources of variation (noise) - between subject variation and - within subject variation This can be illustrated in a schematic fashion as follows: Deterministic factors Diet Time Random Noise within subject between subject Response weight gain The circle of Research Questions arise about a phenomenon A decision is made to collect data Conclusion are drawn from the analysis Statistics Statistics A decision is made as how to collect the data The data is summarized and analyzed The data is collected Notice the two points on the circle where statistics plays an important role: 1.The analysis of the collected data. 2.The design of a data collection procedure The analysis of the collected data. • This of course is the traditional use of statistics. • Note that if the data collection procedure is well thought out and well designed, the analysis step of the research project will be straightforward. • Usually experimental designs are chosen with the statistical analysis already in mind. • Thus the strategy for the analysis is usually decided upon when any study is designed. • It is a dangerous practice to select the form of analysis after the data has been collected ( the choice may to favour certain predetermined conclusions and therefore in a considerable loss in objectivity ) • Sometimes however a decision to use a specific type of analysis has to be made after the data has been collected (It was overlooked at the design stage) The design of a data collection procedure • the importance of statistics is quite often ignored at this stage. • It is important that the data collection procedure will eventually result in answers to the research questions. • And will result in the most accurate answers for the resources available to research team. • Note the success of a research project should not depend on the answers that it comes up with but the accuracy of the answers. • This fact is usually an indicator of a valuable research project.. Some definitions important to Statistics A population: this is the complete collection of subjects (objects) that are of interest in the study. There may be (and frequently are) more than one in which case a major objective is that of comparison. A case (elementary sampling unit): This is an individual unit (subject) of the population. A variable: a measurement or type of measurement that is made on each individual case in the population. Types of variables Some variables may be measured on a numerical scale while others are measured on a categorical scale. The nature of the variables has a great influence on which analysis will be used. . For Variables measured on a numerical scale the measurements will be numbers. Ex: Age, Weight, Systolic Blood Pressure For Variables measured on a categorical scale the measurements will be categories. Ex: Sex, Religion, Heart Disease Types of variables In addition some variables are labeled as dependent variables and some variables are labeled as independent variables. This usually depends on the objectives of the analysis. Dependent variables are output or response variables while the independent variables are the input variables or factors. Usually one is interested in determining equations that describe how the dependent variables are affected by the independent variables A sample: Is a subset of the population Types of Samples different types of samples are determined by how the sample is selected. Convenience Samples In a convenience sample the subjects that are most convenient to the researcher are selected as objects in the sample. This is not a very good procedure for inferential Statistical Analysis but is useful for exploratory preliminary work. Quota samples In quota samples subjects are chosen conveniently until quotas are met for different subgroups of the population. This also is useful for exploratory preliminary work. Random Samples Random samples of a given size are selected in such that all possible samples of that size have the same probability of being selected. Convenience Samples and Quota samples are useful for preliminary studies. It is however difficult to assess the accuracy of estimates based on this type of sampling scheme. Sometimes however one has to be satisfied with a convenience sample and assume that it is equivalent to a random sampling procedure A population statistic (parameter): Any quantity computed from the values of variables for the entire population. A sample statistic: Any quantity computed from the values of variables for the cases in the sample. Statistical Decision Making • Almost all problems in statistics can be formulated as a problem of making a decision . • That is given some data observed from some phenomena, a decision will have to be made about the phenomena Decisions are generally broken into two types: • Estimation decisions and • Hypothesis Testing decisions. Probability Theory plays a very important role in these decisions and the assessment of error made by these decisions Definition: A random variable X is a numerical quantity that is determined by the outcome of a random experiment Example : An individual is selected at random from a population and X = the weight of the individual The probability distribution of a random variable (continuous) is describe by: its probability density curve f(x). i.e. a curve which has the following properties : • 1. f(x) is always positive. • 2. The total are under the curve f(x) is one. • 3. The area under the curve f(x) between a and b is the probability that X lies between the two values. 0.025 0.02 0.015 f(x) 0.01 0.005 0 0 20 40 60 80 100 120 Examples of some important Univariate distributions 1.The Normal distribution A common probability density curve is the “Normal” density curve - symmetric and bell shaped Comment: If m = 0 and s = 1 the distribution is called the standard normal distribution 0.03 Normal distribution with m = 50 and s =15 0.025 0.02 Normal distribution with m = 70 and s =20 0.015 0.01 0.005 0 0 20 40 60 80 100 120 xm 2 f(x) 1 e 2s 2s 2 2.The Chi-squared distribution with n degrees of freedom 1 (n 2 ) / 2 x / 2 f ( x) n n / 2 x e if x 0 2 2 0.5 0.4 0.3 0.2 0.1 2 4 6 8 10 12 14 Comment: If z1, z2, ..., zn are independent random variables each having a standard normal distribution then 2 2 2 U = z1 z2 zn has a chi-squared distribution with n degrees of freedom. 3. The F distribution with n1 degrees of freedom in the numerator and n2 degrees of freedom in the denominator n 1 n 2 / 2 n1 if x 0 1 x f(x) K x n 2 n1 / 2 n1 n1 n 2 n2 2 where K = n1 n2 2 2 (n1 2)2 0.8 0.7 0.6 F dist 0.5 0.4 0.3 0.2 0.1 0 0 1 2 3 4 5 6 Comment: If U1 and U2 are independent random variables each having Chi-squared distribution with n1 and n2 degrees of freedom respectively then U1 n1 F= U 2 n2 has a F distribution with n1 degrees of freedom in the numerator and n2 degrees of freedom in the denominator 4.The t distribution with n degrees of freedom n1 / 2 x f(x) K 1 n 2 n 1 2 where K = n n 2 0.4 0.3 0.2 0.1 -4 -2 2 4 Comment: If z and U are independent random variables, and z has a standard Normal distribution while U has a Chisquared distribution with n degrees of freedom then t= z U n has a t distribution with n degrees of freedom. • 1. 2. 3. 4. 5. An Applet showing critical values and tail probabilities for various distributions Standard Normal T distribution Chi-square distribution Gamma distribution F distribution The Sampling distribution of a statistic A random sample from a probability distribution, with density function f(x) is a collection of n independent random variables, x1, x2, ...,xn with a probability distribution described by f(x). If for example we collect a random sample of individuals from a population and – measure some variable X for each of those individuals, – the n measurements x1, x2, ...,xn will form a set of n independent random variables with a probability distribution equivalent to the distribution of X across the population. A statistic T is any quantity computed from the random observations x1, x2, ...,xn. • Any statistic will necessarily be also a random variable and therefore will have a probability distribution described by some probability density function fT(t). • This distribution is called the sampling distribution of the statistic T. • This distribution is very important if one is using this statistic in a statistical analysis. • It is used to assess the accuracy of a statistic if it is used as an estimator. • It is used to determine thresholds for acceptance and rejection if it is used for Hypothesis testing. Some examples of Sampling distributions of statistics Distribution of the sample mean for a sample from a Normal popululation Let x1, x2, ...,xn is a sample from a normal population with mean m and standard deviation s Let x x i i n Than x x i i n has a normal sampling distribution with mean mx m and standard deviation sx s n 0 20 40 60 80 100 Distribution of the z statistic Let x1, x2, ...,xn is a sample from a normal population with mean m and standard deviation s Let z xm s n Then z has a standard normal distibution Comment: Many statistics T have a normal distribution with mean mT and standard deviation sT. Then T mT z sT will have a standard normal distribution. Distribution of the c2 statistic for sample variance Let x1, x2, ...,xn is a sample from a normal population with mean m and standard deviation s Let 2 x x i s2 and = sample variance i n 1 xi x 2 s i n 1 = sample standard deviation Let c 2 x i x 2 i s2 (n 1)s 2 s 2 Then c2 has chi-squared distribution with n = n-1 degrees of freedom. The chi-squared distribution 0 .5 0 0 4 8 12 16 20 24 Distribution of the t statistic Let x1, x2, ...,xn is a sample from a normal population with mean m and standard deviation s Let xm t s n then t has student’s t distribution with n = n-1 degrees of freedom Comment: If an estimator T has a normal distribution with mean mT and standard deviation sT. If sT is an estimatior of sT based on n degrees of freedom Then T mT t sT will have student’s t distribution with n degrees of freedom. . t distribution standard normal distribution Point estimation • A statistic T is called an estimator of the parameter q if its value is used as an estimate of the parameter q. • The performance of an estimator T will be determined by how “close” the sampling distribution of T is to the parameter, q, being estimated. • An estimator T is called an unbiased estimator of q if mT, the mean of the sampling distribution of T satisfies mT = q. • This implies that in the long run the average value of T is q. • An estimator T is called the Minimum Variance Unbiased estimator of q if T is an unbiased estimator and it has the smallest standard error sT amongst all unbiased estimators of q. • If the sampling distribution of T is normal, the standard error of T is extremely important. It completely describes the variability of the estimator T. Interval Estimation (confidence intervals) • Point estimators give only single values as an estimate. There is no indication of the accuracy of the estimate. • The accuracy can sometimes be measured and shown by displaying the standard error of the estimate. • There is however a better way. • Using the idea of confidence interval estimates • The unknown parameter is estimated with a range of values that have a given probability of capturing the parameter being estimated. Confidence Intervals • The interval TL to TU is called a (1 - a) 100 % confidence interval for the parameter q, if the probability that q lies in the range TL to TU is equal to 1 - a. • Here , TL to TU , are – statistics – random numerical quantities calculated from the data. Examples Confidence interval for the mean of a Normal population (based on the z statistic). TL x z a / 2 s s to TU x z a / 2 n n is a (1 - a) 100 % confidence interval for m, the mean of a normal population. Here za/2 is the upper a/2 100 % percentage point of the standard normal distribution. More generally if T is an unbiased estimator of the parameter q and has a normal sampling distribution with known standard error sT then TL T z a / 2 s T to TU T z a / 2s T is a (1 - a) 100 % confidence interval for q. Confidence interval for the mean of a Normal population (based on the t statistic). TL x t a / 2 s s to TU x t a / 2 n n is a (1 - a) 100 % confidence interval for m, the mean of a normal population. Here ta/2 is the upper a/2 100 % percentage point of the Student’s t distribution with n = n-1 degrees of freedom. More generally if T is an unbiased estimator of the parameter q and has a normal sampling distribution with estmated standard error sT, based on n degrees of freedom, then TL T t a / 2s T to TU T t a / 2s T is a (1 - a) 100 % confidence interval for q. Common Confidence intervals Situation Sample form the Normal distribution with unknown mean and known variance (Estimating m) (n large) Sample form the Normal distribution with unknown mean and unknown variance (Estimating m)(n small) Confidence interval x za / 2 x ta / 2 Estimation of a binomial probability p pˆ za / 2 Two independent samples from the Normal distribution with unknown means and known variances (Estimating m1 - m2) (n,m large) Two independent samples from the Normal distribution with unknown means and unknown but equal variances. (Estimating m1 - m2) ) (n,m small) Estimation of a the difference between two binomial probabilities, p1-p2 s0 n s n pˆ (1 pˆ ) n x y za / 2 2 s x2 s y n m x y ta / 2 s Pooled pˆ 1 pˆ 2 za / 2 1 1 n m pˆ 1 (1 pˆ 1 ) pˆ 2 (1 pˆ 2 ) n1 n2 Multiple Confidence intervals In many situations one is interested in estimating not only a single parameter, q, but a collection of parameters, q1, q2, q3, ... . A collection of intervals, TL1 to TU1, TL2 to TU2, TL3 to TU3, ... are called a set of (1 - a) 100 % multiple confidence intervals if the probability that all the intervals capture their respective parameters is 1 - a Hypothesis Testing • Another important area of statistical inference is that of Hypothesis Testing. • In this situation one has a statement (Hypothesis) about the parameter(s) of the distributions being sampled and one is interested in deciding whether the statement is true or false. • In fact there are two hypotheses – The Null Hypothesis (H0) and – the Alternative Hypothesis (HA). • A decision will be made either to – Accept H0 (Reject HA) or to – Reject H0 (Accept HA). The following table gives the different possibilities for the decision and the different possibilities for the correctness of the decision • The following table gives the different possibilities for the decision and the different possibilities for the correctness of the decision H0 is true H0 is false Accept H0 Reject H0 Correct Decision Type II error Type I error Correct Decision • Type I error - The Null Hypothesis H0 is rejected when it is true. • The probability that a decision procedure makes a type I error is denoted by a, and is sometimes called the significance level of the test. • Common significance levels that are used are a = .05 and a = .01 • Type II error - The Null Hypothesis H0 is accepted when it is false. • The probability that a decision procedure makes a type II error is denoted by b. • The probability 1 - b is called the Power of the test and is the probability that the decision procedure correctly rejects a false Null Hypothesis. A statistical test is defined by • 1. Choosing a statistic for making the decision to Accept or Reject H0. This statisitic is called the test statistic. • 2. Dividing the set of possible values of the test statistic into two regions - an Acceptance and Critical Region. • If upon collection of the data and evaluation of the test statistic, its value lies in the Acceptance Region, a decision is made to accept the Null Hypothesis H0. • If upon collection of the data and evaluation of the test statistic, its value lies in the Critical Region, a decision is made to reject the Null Hypothesis H0. • The probability of a type I error, a, is usually set at a predefined level by choosing the critical thresholds (boundaries between the Acceptance and Critical Regions) appropriately. • The probability of a type II error, b, is decreased (and the power of the test, 1 - b, is increased) by 1. Choosing the “best” test statistic. 2. Selecting the most efficient experimental design. 3. Increasing the amount of information (usually by increasing the sample sizes involved) that the decision is based. Some common Tests Situation Test Statistic Sample form the Normal distribution with unknown mean and known variance (Testing m) (n large) z n x m0 s Sample form the Normal distribution with unknown mean and unknown variance (Testing m) (n small) t n x m 0 s Testing of a binomial probability p Two independent samples from the Normal distribution with unknown means and known variances (Testing m1 - m2) (n, m largel) z z pˆ p0 p0 (1 p0 ) n x y H0 m m m m p p HA m m m m m m m m m m m m p p p p p p m1 m 2 m1 m 2 2 s x2 s y n m Critical Region z < -za/2 or z > za/2 z > za z <-za t < -ta/2 or t > ta/2 t > ta t < -ta z < -za/2 or z > za/2 z > za z < -za z < -za/2 or z > za/2 m1 m 2 z > za m1 m 2 z < -za Two independent samples from the Normal distribution with unknown means and unknown but equal variances. (Testing m1 - m2) t x y s Pooled m1 m 2 m1 m 2 t < -ta/2 or t > ta/2 1 1 n m m1 m 2 t > ta m1 m 2 t < -ta Estimation of a the difference between two binomial probabilities, p1-p2 z pˆ 1 pˆ 2 1 1 pˆ (1 pˆ ) n n 2 1 p1 p 2 p1 p2 z < -za/2 or z > za/2 p1 p 2 z > za p1 p2 z < -za The p-value approach to Hypothesis Testing In hypothesis testing we need 1. A test statistic 2. A Critical and Acceptance region for the test statistic The Critical Region is set up under the sampling distribution of the test statistic. Area = a (0.05 or 0.01) above the critical region. The critical region may be one tailed or two tailed The Critical region: a/2 a/2 Reject H0 za / 2 0 za / 2 Accept H0 z Reject H0 PAccept H 0 when true P za / 2 z za / 2 1 a PReject H 0 when true Pz za / 2 or z za / 2 a In test is carried out by 1. Computing the value of the test statistic 2. Making the decision a. Reject if the value is in the Critical region and b. Accept if the value is in the Acceptance region. The value of the test statistic may be in the Acceptance region but close to being in the Critical region, or The it may be in the Critical region but close to being in the Acceptance region. To measure this we compute the p-value. Definition – Once the test statistic has been computed form the data the p-value is defined to be: p-value = P[the test statistic is as or more extreme than the observed value of the test statistic] more extreme means giving stronger evidence to rejecting H0 Example – Suppose we are using the z –test for the mean m of a normal population and a = 0.05. Z0.025 = 1.960 Thus the critical region is to reject H0 if Z < -1.960 or Z > 1.960 . Suppose the z = 2.3, then we reject H0 p-value = P[the test statistic is as or more extreme than the observed value of the test statistic] = P [ z > 2.3] + P[z < -2.3] = 0.0107 + 0.0107 = 0.0214 Graph p - value -2.3 2.3 If the value of z = 1.2, then we accept H0 p-value = P[the test statistic is as or more extreme than the observed value of the test statistic] = P [ z > 1.2] + P[z < -1.2] = 0.1151 + 0.1151 = 0.2302 23.02% chance that the test statistic is as or more extreme than 1.2. Fairly high, hence 1.2 is not very extreme Graph p - value -1.2 1.2 Properties of the p -value 1. If the p-value is small (<0.05 or 0.01) H0 should be rejected. 2. The p-value measures the plausibility of H0. 3. If the test is two tailed the p-value should be two tailed. 4. If the test is one tailed the p-value should be one tailed. 5. It is customary to report p-values when reporting the results. This gives the reader some idea of the strength of the evidence for rejecting H0 Multiple testing Quite often one is interested in performing collection (family) of tests of hypotheses. 1. H0,1 versus HA,1. 2. H0,2 versus HA,2. 3. H0,3 versus HA,3. etc. • Let a* denote the probability that at least one type I error is made in the collection of tests that are performed. • The value of a*, the family type I error rate, can be considerably larger than a, the type I error rate of each individual test. • The value of the family error rate, a*, can be controlled by altering the thresholds of each individual test appropriately. • A testing procedure of this nature is called a Multiple testing procedure. A chart illustrating Statistical Procedures Independent variables Dependent Variables Categorical Continuous Categorical Multiway frequency Analysis (Log Linear Model) Discriminant Analysis Continuous Continuous & Categorical ANOVA (single dep var) MANOVA (Mult dep var) ?? MULTIPLE REGRESSION (single dep variable) MULTIVARIATE MULTIPLE REGRESSION (multiple dependent variable) ?? Continuous & Categorical Discriminant Analysis ANACOVA (single dep var) MANACOVA (Mult dep var) ?? Comparing k Populations Means – One way Analysis of Variance (ANOVA) The F test The F test – for comparing k means Situation • We have k normal populations • Let mi and s denote the mean and standard deviation of population i. • i = 1, 2, 3, … k. • Note: we assume that the standard deviation for each population is the same. s1 = s2 = … = sk = s We want to test H 0 : m1 m2 m3 mk against H A : mi m j for at least one pair i, j To test H 0 : m1 m2 m3 mk against H A : mi m j for at least one pair i, j use the test statistic 2 Between 2 Error s F s k n x x i 1 2 i i k 1 k 2 ni 1si ni k i 1 i 1 where xi mean for the i th sample. th si standard deviation for the i sample n1 x1 nk xk x overall mean n1 nk k k the statistic n x x i i 1 2 i is called the Between Sum of Squares and is denoted by SSBetween It measures the variability between samples k – 1 is known as the Between degrees of freedom and k n x x k 1 2 i 1 i i is called the Between Mean Square and is denoted by MSBetween k 2 n 1 s i i the statistic i 1 is called the Error Sum of Squares and is denoted by SSError k n k N k i 1 i is known as the Error degrees of freedom and k n 1 s i 1 i 2 i k ni k i 1 is called the Error Mean Square and is denoted by MSError then MS Between F MS Error The Computing formula for F: Compute ni 1) 2) Ti xij Total for sample i j 1 k k G Ti xij Grand Total i 1 k 3) i 1 ni x ij i 1 j 1 k 5) i 1 j 1 N ni Total sample size k 4) ni 2 Ti i 1 ni 2 Then 1) SS Between 3) 2 Ti G N i 1 ni k 2) 2 k ni k 2 Ti SS Error xij i 1 j 1 i 1 ni 2 SS Between k 1 F SS Error N k The critical region for the F test We reject H 0 : m1 m2 m3 mk if F Fa Fa is the critical point under the F distribution with n1 = k - 1degrees of freedom in the numerator and n2 = N – k degrees of freedom in the denominator Example In the following example we are comparing weight gains resulting from the following six diets 1. Diet 1 - High Protein , Beef 2. Diet 2 - High Protein , Cereal 3. Diet 3 - High Protein , Pork 4. Diet 4 - Low protein , Beef 5. Diet 5 - Low protein , Cereal 6. Diet 6 - Low protein , Pork Gains in weight (grams) for rats under six diets differing in level of protein (High or Low) and source of protein (Beef, Cereal, or Pork) Diet Mean Std. Dev. x x2 1 73 102 118 104 81 107 100 87 117 111 100.0 15.14 1000 102062 2 98 74 56 111 95 88 82 77 86 92 85.9 15.02 859 75819 3 94 79 96 98 102 102 108 91 120 105 99.5 10.92 995 100075 4 90 76 90 64 86 51 72 90 95 78 79.2 13.89 5 107 95 97 80 98 74 74 67 89 58 83.9 15.71 792 839 64462 72613 6 49 82 73 86 81 97 106 70 61 82 78.7 16.55 787 64401 Hence i Ti 1 2 1000 859 3 995 k 4 792 5 839 6 Total (G ) 787 5272 N ni Total sample size 60 i 1 ni k x i 1 j 1 ij 2 479432 Ti 2 467846 i 1 ni k Thus Ti 2 G 2 52722 SS Between 467846 4612.933 N 60 i 1 ni 2 k ni k T 2 SS Error xij i 479432 467846 11586 i 1 j 1 i 1 ni k SS Between k 1 4612.933 / 5 922.6 F 4.3 SS Error N k 11586 / 54 214.56 F0.05 2.386 with n 1 5 and n 2 54 Thus since F > 2.386 we reject H0 The ANOVA Table A convenient method for displaying the calculations for the F-test Anova Table Source d.f. Sum of Squares Between k-1 SSBetween Mean Square MSBetween Within N-k SSError MSError Total N-1 SSTotal F-ratio MSB /MSE The Diet Example Source d.f. Sum of Squares Between 5 Within Total F-ratio 4612.933 Mean Square 922.587 54 11586.000 214.556 (p = 0.0023) 59 16198.933 4.3 Using SPSS Note: The use of another statistical package such as Minitab is similar to using SPSS Assume the data is contained in an Excel file Each variable is in a column 1. Weight gain (wtgn) 2. diet 3. Source of protein (Source) 4. Level of Protein (Level) After starting the SSPS program the following dialogue box appears: If you select Opening an existing file and press OK the following dialogue box appears The following dialogue box appears: If the variable names are in the file ask it to read the names. If you do not specify the Range the program will identify the Range: Once you “click OK”, two windows will appear One that will contain the output: The other containing the data: To perform ANOVA select Analyze->General Linear Model-> Univariate The following dialog box appears Select the dependent variable and the fixed factors Press OK to perform the Analysis The Output Tests of Between-Subjects Effects Dependent Variable: wtgn Source Corrected Model Type III Sum of Squares df Mean Square F Sig. 4612.933(a) 5 922.587 4.300 .002 463233.067 1 463233.067 2159.036 .000 4612.933 5 922.587 4.300 .002 Error 11586.000 54 214.556 Total 479432.000 60 16198.933 59 Intercept diet Corrected Total a R Squared = .285 (Adjusted R Squared = .219) Comments • The F-test H0: m1 = m2 = m3 = … = mk against HA: at least one pair of means are different • If H0 is accepted we know that all means are equal (not significantly different) • If H0 is rejected we conclude that at least one pair of means is significantly different. • The F – test gives no information to which pairs of means are different. • One now can use two sample t tests to determine which pairs means are significantly different Fishers LSD (least significant difference) procedure: 1. Test H0: m1 = m2 = m3 = … = mk against HA: at least one pair of means are different, using the ANOVA F-test 2. If H0 is accepted we know that all means are equal (not significantly different). Then stop in this case 3. If H0 is rejected we conclude that at least one pair of means is significantly different, then follow this by • using two sample t tests to determine which pairs means are significantly different Linear Regression Hypothesis testing and Estimation Assume that we have collected data on two variables X and Y. Let (x1, y1) (x2, y2) (x3, y3) … (xn, yn) denote the pairs of measurements on the on two variables X and Y for n cases in a sample (or population) The Statistical Model Each yi is assumed to be randomly generated from a normal distribution with mean mi = a + bxi and standard deviation s. (a, b and s are unknown) slope = b yi s a + b xi a xi Y = a + bX The Data The Linear Regression Model • The data falls roughly about a straight line. 160 Y = a + bX 140 120 100 unseen 80 60 40 20 0 40 60 80 100 120 140 The Least Squares Line Fitting the best straight line to “linear” data Let Y=a +bX denote an arbitrary equation of a straight line. a and b are known values. This equation can be used to predict for each value of X, the value of Y. For example, if X = xi (as for the ith case) then the predicted value of Y is: yˆ i a bxi The residual ri yi yˆi yi a bxi can be computed for each case in the sample, r1 y1 yˆ1, r2 y2 yˆ 2 ,, rn yn yˆ n , The residual sum of squares (RSS) is n n n RSS ri yi yˆ i yi a bxi 2 i 1 i 1 2 i 1 a measure of the “goodness of fit of the line Y = a + bX to the data 2 The optimal choice of a and b will result in the residual sum of squares n n n RSS ri yi yˆ i yi a bxi 2 i 1 i 1 2 i 1 attaining a minimum. If this is the case than the line: Y = a + bX is called the Least Squares Line 2 The equation for the least squares line n Let 2 S xx xi x i 1 n S yy yi y 2 i 1 n S xy xi x yi y i 1 Computing Formulae: 2 xi n n 2 i 1 2 S xx xi x xi n i 1 i 1 2 n yi n n 2 S yy yi y yi2 i 1 n i 1 i 1 n n S xy xi x yi y i 1 n n xi yi n i 1 i 1 xi yi n i 1 Then the slope of the least squares line can be shown to be: n b S xy S xx x x y i i 1 n y i x x i 1 2 i and the intercept of the least squares line can be shown to be: a y bx y S xy S xx x The residual sum of Squares n n RSS yi yˆi yi a bxi 2 i 1 S xy S yy S xx 2 i 1 2 Computing formula Estimating s, the standard deviation in the regression model : n s y i 1 i yˆ i n2 n 2 y a bx 2 i i 1 i n2 S xy 1 S yy n 2 S xx 2 Computing formula This estimate of s is said to be based on n – 2 degrees of freedom Sampling distributions of the estimators The sampling distribution slope of the least squares line : n b S xy S xx x x y i i 1 n y i x x 2 i i 1 It can be shown that b has a normal distribution with mean and standard deviation mb b and s b s S xx s n x x i 1 2 i Thus z b mb sb bb s S xx has a standard normal distribution, and b mb bb t s sb S xx has a t distribution with df = n - 2 (1 – a)100% Confidence Limits for slope b : bˆ t a /2 s S xx ta/2 critical value for the t-distribution with n – 2 degrees of freedom Testing the slope H 0 : b b 0 vs H A : b b 0 The test statistic is: b b0 t s S xx - has a t distribution with df = n – 2 if H0 is true. The Critical Region Reject H 0 : b b 0 vs H A : b b 0 if b b0 t ta / 2 or t ta / 2 s S xx df = n – 2 This is a two tailed tests. One tailed tests are also possible The sampling distribution intercept of the least squares line : a aˆ y bx y S xy S xx x It can be shown that a has a normal distribution with mean and standard deviation 1 m a a and s a s n x n 2 x x i 1 2 i Thus z a ma sa a a 1 s n x 2 n x x i i 1 has a standard normal distribution and a ma t sa a a 1 s n x 2 n x x i 1 i has a t distribution with df = n - 2 2 2 (1 – a)100% Confidence Limits for intercept a : 2 1 x aˆ ta / 2 s n S xx ta/2 critical value for the t-distribution with n – 2 degrees of freedom Testing the intercept H 0 : a a0 vs H A : a a0 The test statistic is: t 1 s n a a0 x n 2 x x i 1 2 i - has a t distribution with df = n – 2 if H0 is true. The Critical Region Reject H 0 : a a 0 vs H A : a a 0 if a a0 t ta / 2 or t ta / 2 sa df = n – 2 Example The following data showed the per capita consumption of cigarettes per month (X) in various countries in 1930, and the death rates from lung cancer for men in 1950. TABLE : Per capita consumption of cigarettes per month (Xi) in n = 11 countries in 1930, and the death rates, Yi (per 100,000), from lung cancer for men in 1950. Country (i) Australia Canada Denmark Finland Great Britain Holland Iceland Norway Sweden Switzerland USA Xi 48 50 38 110 110 49 23 25 30 51 130 Yi 18 15 17 35 46 24 6 9 11 25 20 50 Great Britain death rates from lung cancer (1950) 45 40 35 Finland 30 25 Switzerland Holland 20 USA Australia Denmark Canada 15 Sweden Norway Iceland 10 5 0 0 20 40 60 80 100 Per capita consumption of cigarettes 120 140 Fitting the Least Squares Line n xi 664 i 1 n yi 226 i 1 2 x i 54,404 i 1 n 2 y i 6,018 i 1 n x y i 1 n i i 16,914 Fitting the Least Squares Line First compute the following three quantities: 664 54404 2 S xx 14322.55 11 S yy 2 226 6018 S xy 664226 16914 3271.82 11 1374.73 11 Computing Estimate of Slope (b), Intercept (a) and standard deviation (s), b S xy S xx 3271.82 0.288 14322.55 226 664 a y bx 0.288 6.756 11 11 S xy 1 s S yy n 2 S xx 2 8.35 95% Confidence Limits for slope b : bˆ t a /2 s S xx 0.288 2.262 8.35 1432255 0.0706 to 0.3862 t.025 = 2.262 critical value for the t-distribution with 9 degrees of freedom 95% Confidence Limits for intercept a : 2 1 x aˆ ta / 2 s n S xx 1 664 11 6.756 2.262 8.35 11 1432255 2 -4.34 to 17.85 t.025 = 2.262 critical value for the t-distribution with 9 degrees of freedom death rates from lung cancer (1950) 50 Great Britain 45 40 35 Finland 30 25 Switzerland Holland 20 USA Australia Denmark Canada 15 Y = 6.756 + (0.228)X Sweden Norway Iceland 10 5 0 0 20 40 60 80 100 120 Per capita consumption of cigarettes 95% confidence Limits for slope 0.0706 to 0.3862 95% confidence Limits for intercept -4.34 to 17.85 140 Testing the positive slope H 0 : b 0 vs H A : b 0 The test statistic is: b0 t s S xx The Critical Region Reject H 0 : b 0 in favour of H A : b 0 if b0 t t0.05 =1.833 s df = 11 – 2 = 9 S xx A one tailed test b0 t s S xx Since 0.288 8.35 41.3 1.833 1432255 we reject H0 : b 0 and conclude HA : b 0 Confidence Limits for Points on the Regression Line • The intercept a is a specific point on the regression line. • It is the y – coordinate of the point on the regression line when x = 0. • It is the predicted value of y when x = 0. • We may also be interested in other points on the regression line. e.g. when x = x0 • In this case the y – coordinate of the point on the regression line when x = x0 is a + b x0 y=a+bx a + b x0 x0 (1- a)100% Confidence Limits for a + b x0 : 1 x0 x a bx0 ta / 2 s n S xx 2 ta/2 is the a/2 critical value for the t-distribution with n - 2 degrees of freedom Prediction Limits for new values of the Dependent variable y • An important application of the regression line is prediction. • Knowing the value of x (x0) what is the value of y? yˆ a x0 x = x is: • The predicted value ofy bwhen 0 aˆestimated bˆx0 aby:. bx0 • This in turn canyˆ be The predictor yˆ aˆ bˆx0 a bx0 • Gives only a single value for y. • A more appropriate piece of information would be a range of values. • A range of values that has a fixed probability of capturing the value for y. • A (1- a)100% prediction interval for y. (1- a)100% Prediction Limits for y when x = x0: 1 x0 x a bx0 ta / 2 s 1 n S xx 2 ta/2 is the a/2 critical value for the t-distribution with n - 2 degrees of freedom Example In this example we are studying building fires in a city and interested in the relationship between: 1. X = the distance of the closest fire hall and the building that puts out the alarm and 2. Y = cost of the damage (1000$) The data was collected on n = 15 fires. The Data Fire 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Distance Damage 3.4 26.2 1.8 17.8 4.6 31.3 2.3 23.1 3.1 27.5 5.5 36.0 0.7 14.1 3.0 22.3 2.6 19.6 4.3 31.3 2.1 24.0 1.1 17.3 6.1 43.2 4.8 36.4 3.8 26.1 Damage (1000$) Scatter Plot 50.0 45.0 40.0 35.0 30.0 25.0 20.0 15.0 10.0 5.0 0.0 0.0 2.0 4.0 Distance (miles) 6.0 8.0 Computations n Fire 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Distance Damage 3.4 26.2 1.8 17.8 4.6 31.3 2.3 23.1 3.1 27.5 5.5 36.0 0.7 14.1 3.0 22.3 2.6 19.6 4.3 31.3 2.1 24.0 1.1 17.3 6.1 43.2 4.8 36.4 3.8 26.1 x i 1 n i 49.2 2 x i 196.16 i 1 n y i 1 n i 396.2 2 y i 11376.5 i 1 n x y i 1 i i 1470.65 Computations Continued n x x i 1 i n 49.2 15 3.28 n y y i 1 i n 396.2 15 26.4133 Computations Continued xi x 2 i 1 n n S xx i 1 i yi y 2 i 1 n n S yy i 1 2 i n 2 49 . 2 196.16 34.784 2 n 2 396 . 2 11376.5 n n xi yi n S xy xi yi i 1 i 1 i 1 15 n 1470.65 49.2396.2 171.114 15 15 911.517 Computations Continued S xy 171.114 ˆ bb 4.92 S xx 34.784 a aˆ y bx 26.4133 4.9193.28 10.28 s S yy S xy2 S xx n2 2 171 . 114 911.517 13 34.784 2.316 95% Confidence Limits for slope b : bˆ t a /2 s S xx 4.07 to 5.77 t.025 = 2.160 critical value for the t-distribution with 13 degrees of freedom 95% Confidence Limits for intercept a : 2 1 x aˆ ta / 2 s n S xx 7.21 to 13.35 t.025 = 2.160 critical value for the t-distribution with 13 degrees of freedom Least Squares Line 60.0 Damage (1000$) 50.0 40.0 30.0 y=4.92x+10.28 20.0 10.0 0.0 0.0 2.0 4.0 Distance (miles) 6.0 8.0 (1- a)100% Confidence Limits for a + b x0 : 1 x0 x a bx0 ta / 2 s n S xx 2 ta/2 is the a/2 critical value for the t-distribution with n - 2 degrees of freedom 95% Confidence Limits for a + b x0 : x0 lower upper 1 2 3 4 5 6 12.87 18.43 23.72 28.53 32.93 37.15 17.52 21.80 26.35 31.38 36.82 42.44 95% Confidence Limits for a + b x0 60.0 Damage (1000$) 50.0 40.0 30.0 20.0 Confidence limits 10.0 0.0 0.0 2.0 4.0 Distance (miles) 6.0 8.0 (1- a)100% Prediction Limits for y when x = x0: 1 x0 x a bx0 ta / 2 s 1 n S xx 2 ta/2 is the a/2 critical value for the t-distribution with n - 2 degrees of freedom 95% Prediction Limits for y when x = x0 x0 lower upper 1 2 3 4 5 6 9.68 14.84 19.86 24.75 29.51 34.13 20.71 25.40 30.21 35.16 40.24 45.45 95% Prediction Limits for y when x = x0 60.0 Damage (1000$) 50.0 40.0 30.0 Prediction limits 20.0 10.0 0.0 0.0 2.0 4.0 Distance (miles) 6.0 8.0 Linear Regression Summary Hypothesis testing and Estimation (1 – a)100% Confidence Limits for slope b : bˆ t a /2 s S xx ta/2 critical value for the t-distribution with n – 2 degrees of freedom Testing the slope H 0 : b b 0 vs H A : b b 0 The test statistic is: b b0 t s S xx - has a t distribution with df = n – 2 if H0 is true. (1 – a)100% Confidence Limits for intercept a : 2 1 x aˆ ta / 2 s n S xx ta/2 critical value for the t-distribution with n – 2 degrees of freedom Testing the intercept H 0 : a a0 vs H A : a a0 The test statistic is: t 1 s n a a0 x n 2 x x i 1 2 i - has a t distribution with df = n – 2 if H0 is true. (1- a)100% Confidence Limits for a + b x0 : 1 x0 x a bx0 ta / 2 s n S xx 2 ta/2 is the a/2 critical value for the t-distribution with n - 2 degrees of freedom (1- a)100% Prediction Limits for y when x = x0: 1 x0 x a bx0 ta / 2 s 1 n S xx 2 ta/2 is the a/2 critical value for the t-distribution with n - 2 degrees of freedom Comparing k Populations Proportions The c2 test for independence The c2 test for independence Situation • • • • We have two categorical variables R and C. The number of categories of R is r. The number of categories of C is c. We observe n subjects from the population and count xij = the number of subjects for which R = i and C = j. • R = rows, C = columns Example Both Systolic Blood pressure (C) and Serum Cholesterol (R) were meansured for a sample of n = 1237 subjects. The categories for Blood Pressure are: <126 127-146 147-166 167+ The categories for Cholesterol are: <200 200-219 220-259 260+ Table: two-way frequency Serum Cholesterol <200 200-219 220-259 260+ Total <127 117 85 119 67 388 Systolic Blood pressure 127-146 147-166 121 47 98 43 209 68 99 46 527 204 167+ 22 20 43 33 118 Total 307 246 439 245 1237 The c2 test for independence c Define Ri xij i th row Total j 1 c Ci xij j th column Total i 1 Eij Ri C j n = Expected frequency in the (i,j) th cell in the case of independence. Then to test H0: R and C are independent against HA: R and C are not independent Use test statistic r c c 2 i 1 j 1 x ij Eij 2 Eij Eij= Expected frequency in the (i,j) th cell in the case of independence. xij= observed frequency in the (i,j) th cell Ri C j n Sampling distribution of test statistic when H0 is true r c c 2 x ij Eij 2 Eij i 1 j 1 - c2 distribution with degrees of freedom n = (r - 1)(c - 1) Critical and Acceptance Region Reject H0 if : c 2 ca2 Accept H0 if : c ca 2 2 Table Expected frequencies, Observed frequencies, Standardized Residuals Serum Cholesterol <200 200-219 220-259 260+ Total c2 = 20.85 <127 96.29 (117) 2.11 77.16 (85) 0.86 137.70 (119) -1.59 76.85 (67) -1.12 388 Systolic Blood pressure 127-146 147-166 130.79 50.63 (121) (47) -0.86 -0.51 104.80 40.47 (98) (43) -0.66 0.38 187.03 72.40 (209) (68) 1.61 -0.52 104.38 40.04 (99) (46) -0.53 0.88 527 204 167+ 29.29 (22) -1.35 23.47 (20) -0.72 41.88 (43) 0.17 23.37 (33) 1.99 118 Total 307 246 439 245 1237 Standardized residuals rij x ij Test statistic r c c 2 Eij Eij x i 1 j 1 ij Eij 2 Eij r c rij2 20.85 i 1 j 1 degrees of freedom n = (r - 1)(c - 1) = 9 c 02.05 16.919 Reject H0 using a = 0.05 Another Example This data comes from a Globe and Mail study examining the attitudes of the baby boomers. Data was collected on various age groups Age group Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) Total Total 398 342 378 286 445 1849 One question with responses In an average week, how many times would you drink alcohol? never once twice three or four times Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) 115 130 136 109 218 135 123 87 74 80 64 38 64 40 45 48 31 57 43 40 36 20 34 20 62 398 342 378 286 445 Total 708 499 251 219 172 1849 Age group Are there differences in weekly consumption of alcohol related to age? five more times Total Table: Expected frequencies three or four five more times Total times Age group never once twice Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) 152.40 130.96 144.74 109.51 170.39 107.41 92.30 102.01 77.18 120.09 54.03 46.43 51.31 38.82 60.41 47.14 40.51 44.77 33.87 52.71 37.02 31.81 35.16 26.60 41.40 398 342 378 286 445 708 499 251 219 172 1849 Total rij Table: Residuals x ij Eij Eij Age group never once twice three or four times Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) -3.029 -0.083 -0.726 -0.049 3.647 2.662 3.196 -1.486 -0.362 -3.659 1.357 -1.237 1.771 0.189 -1.982 0.125 -1.494 1.828 1.568 -1.750 r c c 2 i 1 j 1 x ij Eij Eij five more times -0.168 -2.095 -0.196 -1.280 3.203 2 r c rij2 93.97 i 1 j 1 2 c.05 26.296 for 4 4 16 d . f Conclusion: There is a significant relationship between age group and weekly alcohol use Examining the Residuals allows one to identify the cells that indicate a departure from independence Age group never once twice three or four times Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) -3.029 -0.083 -0.726 -0.049 3.647 2.662 3.196 -1.486 -0.362 -3.659 1.357 -1.237 1.771 0.189 -1.982 0.125 -1.494 1.828 1.568 -1.750 five more times -0.168 -2.095 -0.196 -1.280 3.203 • Large positive residuals indicate cells where the observed frequencies were larger than expected if independent Large negative residuals indicate cells where the observed frequencies were smaller than expected if independent Another question withmany responses In an average week, how times would you surf the internet? 5 to 9 times 10 or more times Age group never 1 to 4 times Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) 48 51 79 92 276 72 82 128 63 71 100 92 76 57 67 178 117 95 74 31 398 342 378 286 445 Total 546 416 392 495 1849 Total Are there differences in weekly internet use related to age? Table: Expected frequencies 5 to 9 times 10 or more times Age group never 1 to 4 times Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) 117.53 100.99 111.62 84.45 131.41 89.54 76.95 85.04 64.35 100.12 84.38 72.51 80.14 60.63 94.34 106.55 91.56 101.20 76.57 119.13 398 342 378 286 445 Total 546 416 392 495 1849 Total rij Table: Residuals x ij Eij Eij Age group never 1 to 4 times Echo (Age 20 – 29) Gen X (Age 30 – 39) Younger Boomers (Age 40 – 49) Older Boomers (Age 50 – 59) Pre Boomers (Age 60+) -6.41 -4.97 -3.09 0.82 12.61 -1.85 0.58 4.66 -0.17 -2.91 r c c 2 i 1 j 1 x ij Eij Eij 5 to 9 times 10 or more times 1.70 2.29 -0.46 -0.47 -2.82 6.92 2.66 -0.62 -0.29 -8.07 2 r c rij2 406.29 i 1 j 1 2 c.05 21.03 for 4 3 12 d. f Conclusion: There is a significant relationship between age group and weekly internet use Echo (Age 20 – 29) 70.0 60.0 50.0 40.0 30.0 20.0 10.0 0.0 never 1 to 4 times 5 to 9 times 10 or more times Gen X (Age 30 – 39) 70.0 60.0 50.0 40.0 30.0 20.0 10.0 0.0 never 1 to 4 times 5 to 9 times 10 or more times Younger Boomers (Age 40 – 49) 70.0 60.0 50.0 40.0 30.0 20.0 10.0 0.0 never 1 to 4 times 5 to 9 times 10 or more times Older Boomers (Age 50 – 59) 70.0 60.0 50.0 40.0 30.0 20.0 10.0 0.0 never 1 to 4 times 5 to 9 times 10 or more times Pre Boomers (Age 60+) 70.0 60.0 50.0 40.0 30.0 20.0 10.0 0.0 never 1 to 4 times 5 to 9 times 10 or more times Next topic: Fitting equations to data Link