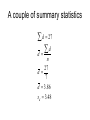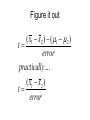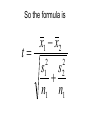Download Comparing Two Groups

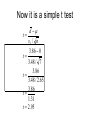
Comparing Two Groups
Statistics 2126
So far..
• We have been able to compare a sample
mean to a population mean
– z test
– t test
• Often times though we have two groups to
compare
• Is Group 1 different from Group 2
Matched pairs or correlated t test
• AKA dependent sample t test
• When subjects are matched on a variable
or are used as their own controls, a sort of
before and after thing if you will
• Be very careful with this
• But it is way powerful and easy to do
Back to our mythical IQ course..
Before
After
Difference
103
98
-5
100
107
7
111
119
8
97
100
3
133
134
1
106
111
5
87
85
-2
A couple of summary statistics
 d  27
d

d 
n
27
d 
7
d  3.86
sd  3.48
Now it is a simple t test
d 
t
sd / n
3.86  0
t
3.48 / 7
3.86
t
3.48 / 2.65
3.86
t
1.31
t  2.95
And now for the decision
•
•
•
•
t(6) = 2.447
tobt = 2.95
Reject H0
Our IQ course works!!
Two sample problems
• While is is useful to know how to compare
a sample mean to a population mean and
check for significance it is not all that
common
• We rarely know μ
– Sometimes we do
• IQ
• Differences
• Theoretical values
The much more common question
is…
• Does one group differ from another?
• Let’s say we had two classes with different
teaching methods
• Is there an effect of teaching method?
Some (made up) data
Statistic
Class 1
Class 2
Mean
77
71
Standard
deviation
6.2
6.7
Number of
students
49
52
Our hypotheses
•
•
•
•
•
•
Are the two classes different?
H 0 μ1 = μ2
H A μ1 ≠ μ2
Or we could restate them like this:
H 0 μ1 - μ2 = 0
H A μ1 ≠ μ2 ≠ 0
Let’s go back to the original t
formula
Statistic
H0
↓
↓
x
t
s/ n
← Error
Figure it out
( x1  x2 )  ( 1   2 )
t
error
practicall y....
( x1  x2 )
t
error
Now about that error…
• We cannot just add
the values of s for
each group
• They must be
weighted
2
1
2
2
s
s

n1 n2
6.2
2
49

6.7
2
52
So the formula is
t
x1  x2
2
1
2
2
s
s

n1 n1
Degrees of freedom
• With a one sample t test we lose one
degree of freedom
• Because we calculated one standard
deviation
• Here was have calculated 2
• So we lose 2 df
• In our case we have 99 df
Sub in the values
t
77  71
2
2
6.2 6.7

49
52
6
t
1.65
t  4.67
rejectH0
conclusions
• All t tests are based on the same formula
• Keep the assumptions in mind
– SRS
– Homogeneity of variance
– Independence of observations