Download PChapter 18 Electromagnetic Induction

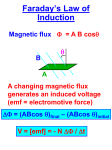
Chapter 18
Electromagnetic Induction
1
Electromagnetic Induction
Induced current:
•
The current generated during the motion of a moving coil in a
stationary magnet.
Induced emf:
•
The emf corresponding to the induced current generated during
the motion of a moving coil in a stationary magnet.
2
Faraday’s Law of Induction:
The induced emf (ε) in a closed loop is equal to the negative of the
time (t) rate of change of magnetic flux (ΦB) through the loop.
dΦ B
ε =−
dt
The magnetic flux dΦB through an infinitesimal area dA is:
B: magnetic field
B⊥
dΦ B = B • A = B⊥ dA = BdA cos θ
Φ B = ∫ B • d A = ∫ BdA cos θ
For a uniform area A:
θ
B||
dA
dΦ B = B⊥ dA
Φ B = B • A = BA cos θ
3
dΦ B
ε =−
dt
This equation shows that a change in flux through
a circuit can induce an emf in a circuit. It is not the
flux itself to induce an emf in a circuit.
Therefore, if the flux through a circuit is constant
(e.g. +ve, -ve, = 0), there will be no induced emf.
For a coil with N identical turns, the total rate of change in flux through all
the turns is equal to N times as that for a single turn. Assuming the flux
varies at the same rate through each turn, the total emf in a coil with N
turns is:
dΦ B
ε = −N
dt
Where, ΦB is the magnetic flux through each turn.
4
Procedures to find the direction of induced emf (ε):
1. define the direction of the area vector A (a positive direction)
2. determine the sign of the magnetic flux (ΦB) and dΦB/dt based on the
direction of A and the magnetic field B.
3. determine the sign of the induced emf or current
•
•
flux increases, dΦB/dt = +ve, ⇒ induced emf or current = -ve
flux decreases, dΦB/dt = -ve, ⇒ induced emf or current = +ve
4. determine the direction of the induced emf or current (right hand rule:
curl right fingers around the area vector A and thumb in the direction
of A)
•
•
induced emf or current is in the same direction as curled fingers,
⇒ induced emf or current = +ve
induced emf or current is in the opposite direction as curled
fingers, ⇒ induced emf or current = -ve
5
A
B
Negative emf
B increases
θ
emf : - ve
ε
initial
magnetic flux more positive
dΦ B
> 0 ⇒ ε is negative
dt
dΦ B
>0
dt
[Φ B ] final > [Φ B ]initial
[Φ B ] final − [Φ B ]initial > 0
final
Q
ΦB > 0
A
emf : - ve
θ
ε
B
B decreases
magnetic flux less negative
ΦB < 0
dΦ B
>0
dt
[Φ B ] final < [Φ B ]initial
[Φ B ] final − [Φ B ]initial > 0
6
A
B
Positive emf
B decreases
θ
emf : + ve
ε
initial
final
ΦB > 0
dΦ B
<0
dt
magnetic flux less positive
Q
dΦ B
< 0 ⇒ ε is positive
dt
A
emf : + ve
θ
ε
B
ΦB < 0
dΦ B
<0
dt
B increases
magnetic flux more negative
7
Example 18.1 (Textbook: 30-2)
A coil of wire containing 500 circular loops with radius 4 cm is placed
between the poles of a large electromagnet, where the magnetic field is
uniform and at an angle of 60o with the plane of the coil. The field
decreases at a rate of 0.2 T/s. What are the magnitude and direction of
the induced emf?
Solution:
The direction for A is chosen as shown in the figure. The
angle between A and B is φ = 30o (not 60o). The flux ΦB
at any time is given by ΦB = BA cos φ, and the rate of
change of flux is dΦB/dt = (dB/dt)A cos φ.
Since dB/dt = -0.2 T/s and A = π(0.04 m)2 = 0.00503 m2,
therefore:
B
A
30o
S
o
60
N
dΦ B dB
=
A cos 30o = (−0.2T / s )(0.00503m 2 )(0.866) dΦ < 0
dt
dt
dt
magnetic flux
= −8.71×10 − 4 Tm 2 / = −8.71×10 − 4 Wb / s
B
less positive
(see previous figure)
8
The induced emf is:
dΦ B
ε = −N
= −(500)(−8.71×10 − 4 Wb / s ) = 0.435V .
dt
When we look in along the coil axis from the left, in the direction of the
area vector A (30o above the magnetic field B), the positive direction for ε
is clockwise, according to the right-hand rule. The emf in this example is
in fact positive and thus is clockwise.
If the ends of the wire are connected together, the direction of current
in the coil is clockwise. A clockwise current gives added magnetic field
through the coil in the same direction as the flux from the
electromagnet, and therefore tends to oppose the decreases in total
flux.
9
In-Class Exercise 18.1
The square coil has sides L = 0.25m long and is tightly wound with N = 200 turns of wire. The
resistance of the coil is R = 5Ω. The coil is placed in a spatially uniform magnetic field that is
directed perpendicular to the face of the coil and whose magnitude is decreasing at a rate
dB/dt = 0.04 T/s.
(a)
What is the magnitude of the emf induced in the coil?
(b)
What is the magnitude of the current circulating through the coil?
Solution:
(a)
The flux through one turn is Φm = BA = BL 2
By Faraday’s law,
d Φm
|ε
ε| = |- N
|
dt
=NL
2
dB
dt
= (200) (0.25m)2 (0.040 T/s)
= 0.50 V
(b)
The magnetic of the current induced in the coil is
ε
0.50V
I=
=
= 0.10 A
R
5.0 Ω
10
In-Class Exercise 18.2
A magnitude field B is directed perpendicular to the plane of a circular coil of radius
r = 0.5m. The field is cylindrically symmetric with respect to the center of the coil,
and its magnitude decays exponentially according to B = 1.5e-5t, where B is in teslas
and t is in seconds.
(a) Calculate the emf induced in the coil at the times t1= 0s, t2= 5x10-2s, and t3= 1s.
(b) Determine the current in the coil at these three times if its resistance is 10 Ω.
Solution:
(a)
Given r = 0.50 m, B = 1.5e-5.0t
By Φm = BA = Bπr 2
= (1.5e-5.0t T)π(0.50 m) 2
= 1.2e-5.0t Wb
From Faraday’s law, the magnitude of the induced emf is
ε= |
dΦm
dt
| = 6.0 e-5.0t V
So, we have
At t1 = 0 s, ε= 6.0 V;
At t2 = 5.0 x 10-2 s, ε= 4.7 V;
At t3 = 1.0 s, ε= 0.04 V;
11
Lenz’s Law:
H. F. E. Lenz (1804 – 1865)
The direction of any magnetic induction effect is such as to oppose the cause of
the effect.
Possible causes:
•
changing flux through a stationary circuit due to a varying magnetic field
•
changing flux due to motion of the conductors that make up the circuit
•
other combinations
1
2
(a)
1
1
(c)
(b)
2
2
12
In an adjustable coil, current can be changed. A change of current in the
coil induces an emf.
The coil is called “inductor”. Symbol:
The relationship between current and emf is described by “inductance”
For a number of coils, the coupling between coils is described by “mutual
inductance”
coil 1 (N1 turns)
B
ε 2 = −N2
dt
Φ B2 is proportional to i1 :
N 2 Φ B2 = Mi1
N2
dΦ B2
i1
coil 2 (N2 turns)
dΦ B2
M=
di1
=M
dt
dt
N 2 Φ B2
i1
M : mutual inductance of coil 1 and 2
13
Mutually induced emf:
dΦ B1
di2
= −M
ε 1 = − N1
dt
dt
dΦ B2
di1
ε 2 = −N2
= −M
dt
dt
For the design of a multiple circuit
system, mutual inductance is kept to
be as small as possible to minimize
nuisance due to mutual inductance.
Mutual inductance:
M=
N 2 Φ B2
i1
=
N1Φ B1
i2
The unit of mutual inductance M is “henry” or (1 H)
SI unit
1 H = 1 Wb/A = 1 Ωs = 1 J/A2 = 1 Vs/A
14
Self-inducated emf:
For a single isolated circuit, the current in the circuit sets up a magnetic
field that causes a magnetic flux through the same circuit. When the
current changes, the flux changes. Therefore, a circuit with varying
current will have an emf inducted in it by varying its own magnetic field.
Such emf is called self-induced emf.
The self-inductance (L) of a circuit = magnitude of the self-induced emf
per unit rate of change of current.
ΦB
L=N
i
N = N turns of a coil
The self-inducated emf is:
di
ε = −L
dt
15
The energy (U) associated magnetic field of an inductor with inductance
L and current I is:
1 2
U = LI
2
Energy stored in an inductor
The magnetic energy density u (energy per unit volume) is:
B2
u=
2µ0
B : magnetic field (T)
µ0 = 4π × 10-7 (Ns2/C2)
(the field is in vacuum)
16
Example 18.2
An induced emf of 2 V is measured across a coil of 50 closely wound turns while
the current through it increases uniformly from 0 to 5 A in 0.1s.
(a) What is the self-inductance of the coil?
(b) With the current at 5 A, what is the flux through each turn of the coil?
Solution:
(a)
Ignoring the negative sign and calculate the magnitude only, we have
2.0 V
ε
L=
=
5.0 A / 0.10 s
dI / dt
= 4.0 × 10-2 H
(b)
By
NΦm = L I, we have
Φm =
LI
=
(4.0 × 10-2 H) (5.0 A)
N
= 4.0 × 10-3 Wb
50
17